ワイエルシュトラスのペー関数

ワイエルシュトラスのペー関数は，楕円関数の代表例です。ただし，楕円関数の定義は以下のとおりです：

• 「二重周期」の意味は後述します。

• 有理型関数とは，特異点が離散的で，真性特異点を持たない関数のことです。例えば，多項式の有理式の形の関数 $\left( \dfrac{1}{x(x+1)} \text{など} \right)$ や三角関数の有理式$\left( \dfrac{1}{\sin x}\text{など} \right)$ は有理型です。→偏角の原理とルーシェの定理～方程式の解の個数について
  ペー関数は，特異点が $\Lambda$ の各点のみで，それらはすべて位数が $2$ の極なので有理型関数です。

微分

ペー関数の導関数を計算しましょう。ペー関数は一様収束します （証明は ワイエルシュトラスのペー関数～証明編 参照）。

よって，項別微分できるので， $$\wp' (z) = -\sum_{\omega \in \Lambda} \dfrac{2}{(z - \omega)^3}$$ となります。

ペー関数は偶関数

定義より $\wp (-z) = \wp (z)$ なので，ペー関数は偶関数 です。

二重周期関数

ペー関数の非常に重要な性質に周期性があります。

格子

複素数 $\omega_1 , \omega_2$ は $\dfrac{\omega_1}{\omega_2} \notin \mathbb{R}$ を満たすとします。

このとき，格子 $\Lambda$ を $$\Lambda = \{ n \omega_1 + m \omega_2 : n,m \in \mathbb{Z} \}$$ と定めます。

格子は下図の黒点です。

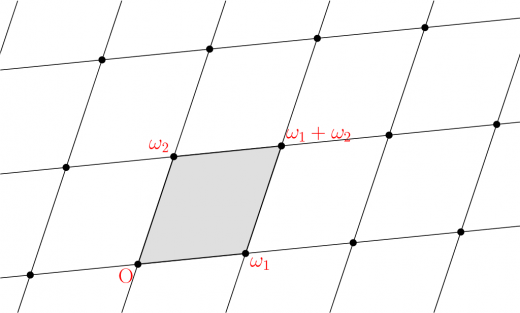
また，$\{ s \omega_1 + t \omega_2 : s,t \in [0,1] \}$ すなわち，$\mathrm{O}$，$\omega_1$，$\omega_2$，$\omega_1 + \omega_2$ で囲まれた平行四辺形を単位格子と呼びます。

ペー関数の周期性

$$\begin{aligned} &(\wp (z+\omega_1) - \wp (z))'\\ &= - \sum_{\omega \in \Lambda} \dfrac{2}{(z + \omega_1 - \omega)^3} + \sum_{\omega \in \Lambda} \dfrac{2}{(z - \omega)^3}\\ &= 0 \end{aligned}$$

より $\wp (z+\omega_1) - \wp (z)$ は定数です。これを $c$ としましょう。

$z = -\dfrac{\omega_1}{2}$ を代入すると $c = \wp \left( \dfrac{\omega_1}{2} \right) - \wp \left( -\dfrac{\omega_1}{2} \right)$ です。

ペー関数は偶関数であったため $c = 0$ となり $\wp (z) = \wp (z+ \omega_1)$ です。

同様に， $\wp (z) = \wp (z+ \omega_2)$ です。

このように2つの周期を持つ関数（比が実数でない2つの複素数 $\omega_1,\omega_2$ に対して $\wp(z)=\wp(z+\omega_1)+\wp(z+\omega_2)$ を満たす関数）のことを二重周期関数といいます。

特に有理型の二重周期関数を楕円関数といいます。

極

定義より，ペー関数の極は $\Lambda$ の点となります。特に定義式から極の位数は $2$ です。

※ 位数について →ローラン展開 を参照。

零点

ペー関数の零点を計算するのは難しいです。しかし，$\wp'$ の零点は簡単にわかります。

ちなみに $\wp'$ の零点はこれで尽くされます。

なお，以上の議論より，一般に（$P(a)$ 内で）二重周期関数の零点と極の個数は一致することがわかります。

$\wp (z) = c$ の解

$\wp (z) = \wp (z_0)$ の解

$z_0$ を格子点以外の点とします。$\wp (z) = \wp (z_0)$ となる $z$ を調べてみましょう。

簡単のため，$z , z_0$ は単位格子の中として考えます。

$$\begin{aligned} \wp (z_0) &= \wp (-z_0) &(\text{偶関数の性質})\\ &= \wp (- z_0 + \omega_1) &(\text{周期性}) \end{aligned}$$ となります。同様に $-z_0 + \omega_2$，$-z_0 + \omega_1 + \omega_2$ も解になります。

このうち同じ単位格子の中にある点は1点のみです。

$\wp (z) = \wp (z_0)$ の解はこの他にはありません。

実際 $g (z) = \wp (z) - \wp (z_0)$ とおくと，これは二重周期関数であるため，（格子内の）零点と極の個数は一致します。$g$ は格子点で2位の極を持つため，零点は高々2個です。こうして示されました。

ペー関数は任意の複素数値を取る

実際，$f(z) = \wp (z) - c$ とおき，同様の議論を適用すると零点が存在することがわかります。

等式

ペー関数には重要な等式があります。

特に $\wp'$ は $z = \dfrac{\omega_1}{2} , \dfrac{\omega_2}{2} , \dfrac{\omega_1 + \omega_2}{2}$ で零点を取るため $$\begin{aligned} &\{ \wp'(z) \}^2\\ &= 4 \left( \wp (z) - \wp \left( \dfrac{\omega_1}{2} \right) \right) \left( \wp (z) - \wp \left( \dfrac{\omega_2}{2} \right) \right) \left( \wp (z) - \wp \left( \dfrac{\omega_1 + \omega_2}{2} \right) \right) \end{aligned}$$ となります。

証明はワイエルシュトラスのペー関数～証明編をご覧ください。

格子から得られる楕円曲線

楕円曲線 とは，$y^2 = (x\ \text{の3次式})$ と表される曲線でした。

ここで $(x,y) = \left( \wp(z) , \wp'(z) \right)$ おくと，ペー関数の微分方程式から $(x,y)$ は $$y^2 = 4 x^3 - g_2 x - g_3$$ を満たします。

これはペー関数によって楕円曲線をパラメタ表示できることを意味します。

単位格子と楕円曲線

格子 $\Lambda$ に対するペー関数 $\wp (z)$ によって得られる楕円曲線を $C_{\Lambda}$ とおきましょう。

上で述べたパラメタ付けは「良い」パラメタ付けです。特に次の命題が成り立ちます。

証明はワイエルシュトラスのペー関数～証明編をご覧ください。

ペー関数を通して「格子 → 楕円曲線」という流れが見つかりました。逆に楕円曲線から格子を復元できるでしょうか。

実は次の命題が成立します。（※ 証明には複素解析と微分形式の知識が必要になるので飛ばします。）

こうしてペー関数は楕円曲線と基本格子をつなぐ架け橋となります。

特に基本格子は「トーラス（円環の表面）」とみなすことができ，楕円曲線は（無限遠点を加えると）ドーナツ状になっていることが知られています。興味がある方は，楕円曲線論や複素曲線論を勉強してみてください。

格子とワイエルシュトラスのペー関数に関連した様々な関数について紹介します。

ツェータ関数

ペー関数は格子点で2位の極を持つのでした。ここでは格子点で1位の極を持つ関数を考えてみましょう。

そのためにペー関数の原始関数を考えます。

定義から $$\zeta' (z) = - \wp (z)$$ となります。このようにツェータ関数はペー関数を「項別積分」したものとなります。

擬周期性

$\zeta (z)$ に周期性はあるのでしょうか。

$\zeta (z + \omega_1) - \zeta (z) = \wp' (z+\omega_1) - \wp' (z) = 0$ です。

よって，$\zeta (z + \omega_1) - \zeta (z)$ は定数となります。

$\zeta (z + \omega_2) - \zeta (z)$ もまた定数となります。

このような関数を擬周期関数といいます。

シグマ関数

次は格子点を零点に持つ関数を考えてみましょう。

ツェータ関数の「積分」を考えます。

次の関数等式が成り立ちます。