入試数学コンテスト第7回第6問解答解説

$D_1$ は不等式$$(x-p)^2+y^2 \leq r^2$$で表される領域を $y$ 軸について回転させた図形である。

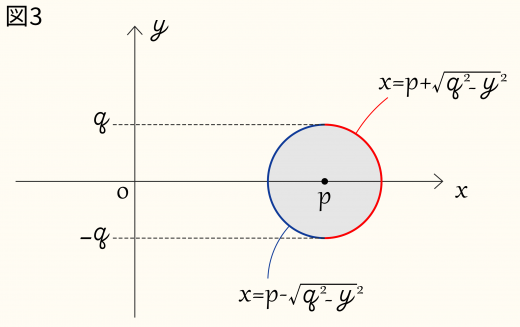
$p \geq q$ だから，領域の境界は図のように $x=p \pm \sqrt{q^2-y^2}$ という曲線であり，$$\frac{dx}{dy}=\pm \frac{y}{\sqrt{r^2-y^2}}$$である。

よって $D_1$ の表面積 $S$ は $$\begin{aligned} S&=\int_{-q}^{q}2\pi\left(p+\sqrt{q^2-y^2}\right)\sqrt{1+\frac{y^2}{q^2-y^2}}dy\\ &\quad +\int_{-q}^{q}2\pi\left(p-\sqrt{q^2-y^2}\right)\sqrt{1+\frac{y^2}{q^2-y^2}}dy\\ &=2\pi\int_{-q}^{q}2p\sqrt{\frac{q^2}{q^2-y^2}}dy\\ &=4\pi pq\int_{-q}^{q}\frac{dy}{\sqrt{q^2-y^2}}\\ &=4\pi pq \int_{-\pi/2}^{\pi/2} \frac{q\cos \theta d\theta}{q \cos \theta}\\ &=4\pi^2pq \end{aligned}$$ である。ただし途中で$y=q\sin\theta$として置換積分した。

また体積$V$は $$\begin{aligned} V&=\int_{-q}^q \pi \left(p+\sqrt{q^2-y^2}\right)^2dy\\ &\quad-\int_{-q}^q \pi \left(p-\sqrt{q^2-y^2}\right)^2dy\\ &=\pi \int_{-q}^q 4p\sqrt{q^2-y^2}dy\\ &=4\pi p \cdot \frac{1}{2}\pi q^2\\ &=2\pi^2 pq^2 \end{aligned}$$ である。ただし途中で $\int_{-q}^q \sqrt{q^2-y^2}dy$ が半径 $q$ の半円の面積であることを使った。

$q>p$ のとき，原点中心で半径が $q-p,q+p$ の球をそれぞれ $B(q-p),B(q+p)$ とおくと，上の図より $$B(q-p) \subset D_1 \subset B(q+p)$$が成り立つ。同様に $$B(q-p) \subset D_2 \subset B(q+p)$$ $$B(q-p) \subset D_3 \subset B(q+p)$$も成り立つから，これらより $$B(q-p) \subset D_1 \cup D_2 \cup D_3 \subset B(q+p)$$となるから，体積を考えると $$\frac{4}{3}\pi(q-p)^3 \leq V(p,q) \leq \frac{4}{3}\pi(q+p)^3$$が成り立つ。（下につづく。）

上の不等式より$$\lim_{q \to \infty} \dfrac{V(p,q)}{p^a q^b}$$が $0$ でない値に収束するためには $b=3$ が必要で，そのときはさみうちの原理より $$\lim_{q \to \infty} \dfrac{V(p,q)}{p^a q^3} =\frac{4\pi}{3p^a}$$である。さらにこれが $\lim_{p \to \infty}$ で $0$ でない値に収束するためには $a=0$ が必要である。以上より $a=0,b=3$ で求める極限値は$$\lim_{p \to \infty} \left( \lim_{q \to \infty} \dfrac{V(p,q)}{p^0 q^3} \right) = \frac{4}{3}\pi$$である。

$q$ を固定して $p$ を大きくしたとき，$D_1$ と $D_2$ の交わり $D_1\cap D_2$ は2つの部分に分かれるが，どちらも「半径 $q$ の円柱2つが直角に交わるときにできる図形」に近づいていく。その体積は1辺 $2q$ の立方体の体積以下だから，$8q^3$ 以下である。よって$D_1 \cap D_2$ の体積は $p$が十分大きいとき定数$C$により $Cq^3$ 以下になる。他のドーナツの交わりも同様だから，$p$ が $q$ に 比べて十分大きいとき（定数$C$をとりなおして）$$|V(p,q)-6\pi^2pq^2| \leq Cq^3$$ が成り立つ。（ドーナツ 1個の体積は (1) より $2\pi^2pq^2$ であることに注意。）

よって$$6\pi^2pq^2-Cq^3 \leq V(p,q) \leq 6\pi^2pq^2+Cq^3$$だから， $$\lim_{p \to \infty} \dfrac{V(p,q)}{p^c q^d}$$が $0$ でない値に収束するためには $c=1$ が必要で，そのとき不等式より $$\lim_{p \to \infty} \dfrac{V(p,q)}{p^1 q^d} =6\pi^2q^{2-d}$$となる。つまり求める $c,d$ は $c=1,d=2$ で，そのとき$$\lim_{p \to \infty} \dfrac{V(p,q)}{p^1 q^2}=6\pi^2$$ となる。

まず$D_i$たちは $$D_1 \colon \left(\sqrt{x^2+z^2}-p\right)^2+y^2\leq q^2$$ $$D_2 \colon \left(\sqrt{y^2+x^2}-p\right)^2+z^2\leq q^2$$ $$D_3 \colon \left(\sqrt{z^2+y^2}-p\right)^2+z^2\leq q^2$$と表せる。よって$D_1 \cap D_2 \cap D_3$は連立不等式 $$\begin{aligned} \left(\sqrt{x^2+z^2}-p\right)^2+y^2 &\leq q^2\\ \left(\sqrt{y^2+x^2}-p\right)^2+z^2 &\leq q^2\\ \left(\sqrt{z^2+y^2}-p\right)^2+x^2 &\leq q^2 \end{aligned}$$で表される領域である。

$p>\sqrt{3}q$ が必要十分であることを示す。

• 必要性

$D_1 \cap D_2 \cap D_3 = \emptyset$ ならば $D_1 \cap D_2 \cap D_3$ と直線 $x=y=z$ の交わりも $\emptyset$ である。よって連立不等式に $x=y=z$ を代入した$$\left(\sqrt{x^2+x^2}-p\right)^2+x^2\leq q^2$$が実数解を持たないことが必要。変形すると$$3x^2-2\sqrt{2}p|x|+p^2-q^2\leq 0$$$$3\left(|x|-\frac{\sqrt{2}}{3}p\right)^2+\frac{1}{3}p^2-q^2 \leq 0$$となる。$\frac{\sqrt{2}}{3}p>0$ に注意すると，これが実数解を持たないための条件は$$\frac{1}{3}p^2-q^2>0$$つまり $p>\sqrt{3}q$ となる。よって $p>\sqrt{3}q$ が必要である。

• 十分性

$p>\sqrt{3}q$ のとき $D_1 \cap D_2 \cap D_3 = \emptyset$ であることを示す。$D_1 \cap D_2 \cap D_3$ が空集合かどうかは図形を拡大縮小しても変わらない，つまり $p$ と $q$ の比 $p/q$ のみによって決まるから，$p=1$ としてよい。

背理法で示す。$p=1>\sqrt{3}q$ つまり $p=1,q<\frac{1}{\sqrt{3}}$ のときに連立不等式$$\begin{aligned} \left(\sqrt{x^2+z^2}-1\right)^2+y^2 &\leq q^2\\ \left(\sqrt{y^2+x^2}-1\right)^2+z^2 &\leq q^2\\ \left(\sqrt{z^2+y^2}-1\right)^2+z^2 &\leq q^2 \end{aligned}$$が実数解$(x,y,z)$を持ったと仮定する。これらを全て足して展開すると$$3(x^2+y^2+z^2)-2\left(\sqrt{x^2+z^2}+\sqrt{y^2+x^2}+\sqrt{z^2+y^2}\right)+3\leq 3q^2$$となる。$q<\frac{1}{\sqrt{3}}$と合わせると$$3(x^2+y^2+z^2)-2\left(\sqrt{x^2+z^2}+\sqrt{y^2+x^2}+\sqrt{z^2+y^2}\right)+3<1$$が成り立つ。ここで $A=\sqrt{x^2+z^2},B=\sqrt{y^2+x^2},C=\sqrt{z^2+y^2}$ とおくと$$2x^2+2y^2+2z^2=A^2+B^2+C^2$$だから不等式は$$\frac{3}{2}(A^2+B^2+C^2)-2(A+B+C)+2<0$$と書ける。ここでコーシーシュワルツの不等式より$$(A+B+C)^2 \leq 3(A^2+B^2+C^2)$$だから，この2つの不等式を合わせると$$\frac{1}{2}(A+B+C)^2-2(A+B+C)+2<0$$が成り立つ。しかし左辺は$$\frac{1}{2}(A+B+C-2)^2 \geq 0$$だから矛盾する。よって背理法により $p >\sqrt{3}q$ のとき $D_1 \cap D_2 \cap D_3 = \emptyset$ である。