正規分布の基礎的な知識まとめ

更新 2021/03/07

正規分布の基本的な知識を整理しました。

正規分布とは

正規分布（ガウス分布）とは，図のような左右対称の連続型の確率分布です。正確な定義（確率密度関数）については後述します。
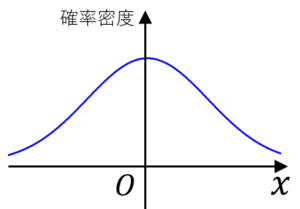
正規分布は最も代表的な分布の一つです。例えば物理などの実験における測定の誤差，テストの点数などは（ほぼ）正規分布に従う（ことが多い）と考えられています。
また，コイン投げのように，反復試行の成功回数が従う確率分布も（反復試行が多いとき，近似的に）正規分布になります。→二項分布の正規近似（ラプラスの定理）
この記事では，正規分布について，確率密度関数の式の意味や，平均・分散の導出を中心に解説します。

正規分布の確率密度関数

正規分布の確率密度関数について解説します。
前提知識：確率密度関数の意味と具体例
正規分布（ガウス分布）の確率密度関数は，
f(x)=12πσexp⁡{−(x−μ)22σ2}f(x)=\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left\{-\dfrac{(x-\mu)^2}{2\sigma^2}\right\}f(x)=2π​σ1​exp{−2σ2(x−μ)2​}
です。平均は
μ\muμ，分散は
σ2\sigma^2σ2
 です。
正規分布の確率密度関数は複雑そうですが，基本形を考えればだいぶ簡単になります。正規分布の中でも平均が μ=0\mu=0μ=0，分散が σ2=1\sigma^2=1σ2=1 であるようなものが特に重要で，標準正規分布と呼ばれます。標準正規分布の確率密度関数は，f(x)=12πe−x22f(x)=\dfrac{1}{\sqrt{2\pi}}e^{-\tfrac{x^2}{2}}f(x)=2π​1​e−2x2​ です。だいぶ簡単になりましたね。
標準正規分布のグラフは図のようになります。例えば 000 以上 aaa 以下となる確率は斜線部分の面積になります。
なお，指数関数 eAe^{A}eA において AAA が複雑な式のとき書きづらいので exp⁡(A)\exp(A)exp(A) と書いています。
補足多変数バージョン：多変量正規分布の確率密度関数の解説
標準正規分布の重要性：正規分布の標準化の意味と証明

1シグマ区間

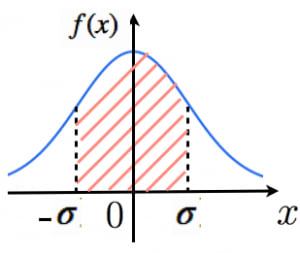
正規分布において $[-\sigma,\sigma]$ を「1シグマ（ $1\sigma$ ）区間」と言います。1シグマ区間に入る確率は約68％です。偏差値40から60に相当します。→偏差値の意味・目安・5つの性質
同様に， $[-k\sigma,k\sigma]$ を「 $k$ シグマ区間」と言います。2シグマ区間に入る確率は約95％，3シグマ区間に入る確率は約99.7％です。偏差値20から80の間に約99.7％の人間がいるということになります。

正規分布とガウス積分

ガウス積分を用いて3つの重要な性質を証明していきます（→ガウス積分の公式の2通りの証明）。以下の3つ（正規化・平均・分散）を理解すれば，正規分布 $f(x)$ の確率密度関数がなぜ複雑そうな形をしているのかが分かります。

1（規格化・正規化）：正規分布の確率密度関数が本当に確率密度関数であること（全区間で積分すると $1$ となること）を確認します。

証明

$\displaystyle\int_{-\infty}^{\infty}f(x)dx=\dfrac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{\infty}\exp\left\{-\dfrac{(x-\mu)^2}{2\sigma^2}\right\}dx$

ここで， $x-\mu=y$ と置換すると，上式は

$\dfrac{1}{\sqrt{2\pi}\sigma}\times\int_{-\infty}^{\infty}\exp\left(-\dfrac{y^2}{2\sigma^2}\right)dy$ この定積分の値はガウス積分の公式より $\sqrt{2\sigma^2\pi}$ となるので確かに $f(x)$ を全区間で積分すると $1$ となる。

※ 積分区間が $-\infty$ から $\infty$ なので平行移動しても積分区間は変わりません。

正規分布の平均

2（期待値）： $f(x)$ で表される正規分布の期待値（平均） $E[X]$ が $\mu$ であることを証明してみます。これは分布が $x=\mu$ に関して対称な形をしていることから明らかですが，積分の練習として。

証明

期待値の定義より， $E[X]=\displaystyle\int_{-\infty}^{\infty}xf(x)dx$

ここで， $x-\mu=y$ と置換すると，

$\begin{aligned}E[X]&=\displaystyle\int_{-\infty}^{\infty}(y+\mu)f(y+\mu)dy\\ &=\displaystyle\int_{-\infty}^{\infty}yf(y+\mu)dy+\mu\int_{-\infty}^{\infty}f(y)dy\end{aligned}$

第一項の被積分関数は奇関数×偶関数＝奇関数なので積分値は $0$ ，第二項の積分値はさきほど確認したように $1$ なので結局 $E[X]=\mu$ となる。

正規分布の分散・標準偏差

3（分散・標準偏差）： $f(x)$ で表される正規分布の分散 $V[X]$ が $\sigma^2$ であること，つまり標準偏差が $\sigma$ であることを証明してみます。

証明

分散の定義より， $V[X]=\displaystyle\int_{-\infty}^{\infty}(x-\mu)^2\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left\{-\dfrac{(x-\mu)^2}{2\sigma^2}\right\}dx$

ここで， $x-\mu=y$ と置換すると

$V[X]=\dfrac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{\infty}y^2\exp\left(-\dfrac{y^2}{2\sigma^2}\right)dy$

よって，ガウス積分の公式（→ガウス積分の公式の2通りの証明の公式3）より $V[X]=\dfrac{1}{\sqrt{2\pi}\sigma}\times\sqrt{2\pi}\sigma^3=\sigma^2$

正規分布の確率密度関数は全区間で積分すると1，平均が $\mu$ ，分散が $\sigma^2$ となるようにうまく作られていることが分かりました！

偏差値80を越えるのがいかに難しいかが分かります。

Tag:数検1級の範囲と必要な公式まとめ

この記事の監修者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！