証明の方針
-
三角形 ABC の情報(角度,長さ)で表す。
-
辺の情報と角度の情報が混在していると複雑になるので,辺の情報は正弦定理で角度の情報に変換する(外接円の半径
R
は
A,B,C
に関して対称なので扱いやすい)。
-
AR
の形を見て三倍角の公式の発展形(因数分解した形)がひらめくとです(→三倍角の公式:基礎からおもしろい発展形まで)。ここがこの証明一番の難所。
証明
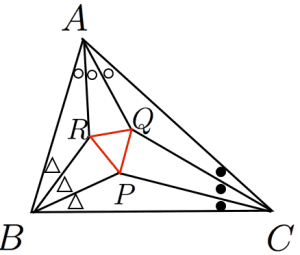
三角形
ARB
に正弦定理を用いて
AR
を三角形
ABC
の情報で表す:
AR=sin(π−3A−3B)csin(3B)=sin(3A+B)csin(3B)=2RsinCsin(3π−C)sin(3B)
ただし,最後の変形で三角形
ABC
に正弦定理を用いた。
ここで,変形三倍角の公式:
sinC=4sin3Csin(3π−C)sin(3π+C)
を用いると
AR=8Rsin3Bsin3Csin(3π+C)
同様にして,
AQ=8Rsin3Bsin3Csin(3π+B)
出てきた式より,
sin(3π+B)AQ=sin(3π+C)AR
が分かるので,補足1から,
∠ARQ=3π+B,∠AQR=3π+C
が分かる。他の角も同様に求めることができ,
∠PQR=∠QRP=∠RPQ=3π
が分かる(→補足2)。
補足1:
∠ARQ,∠AQR
は,
∠ARQ+∠AQR=π−3A=32π+B+C
および,正弦定理から
sin∠ARQAQ=sin∠AQRAR
という2つの式を満たす。
これを,∠ARQ,∠AQR
の連立方程式とみなすと,(3π+B,3π+C)
が解になっていることが,上記の証明中の議論から分かる。
そして,それ以外の解が(0<∠ARQ<π
の範囲で)存在しないことも分かる(1つめの式を
∠AQR
について解いて,2つめの式に代入して変形していくと確認できる)
補足2:例えば,
∠QRP=2π−∠ARB−∠ARQ−∠BRP=2π−(π−3A−3B)−(3π+B)−(3π+A)=3π
フランクモーリーの定理は,最も美しくて実用性のない初等幾何の定理の1つです。
Tag:とにかく美しい数学公式まとめ













