組み合わせ論による q-二項係数の定義
更新
-整数,-階乗,-二項係数を順に と定義する。
上記の定義の詳細は,q-二項係数とq-二項定理 で紹介しています。
この記事では,上記のような「整数の 類似」が組み合わせ論的にも定義できることを示します。
転倒数
転倒数
数列 に対して,転倒数とは をいう。
例えば の転倒数を数えましょう。
となっているのは
- に対して
- に対して
- に対して
- に対して
であるため,転倒数は です。
-階乗
-階乗
計算例
を計算する。
- 転倒数 :
- 転倒数 :
- 転倒数 :
- 転倒数 :
よって
証明
実際に冒頭の定義と一致することを示しましょう。
帰納的に証明する。
のときは明らかである。
で成立することを仮定する。
の順列 に を挿入する方法は 通りあり,各操作で増える転置数をまとめると次のようになる。
- の手前に挿入:転置数が 増える。
- の手前に挿入:転置数が 増える。
- ……
- の手前に挿入:転置数が 増える。
- の後ろに挿入:転置数が 増える。
よって を挿入することで
となる。
は そのものである。こうして であるため,命題が従う。
-二項係数
-二項係数
を 個, を 個並べた数字の列のうち,転倒数が のものの個数を とおく。
-二項係数 を次のように定義する。
計算してみましょう。
を計算する。
- 転倒数 :
- 転倒数 :
- 転倒数 :
- 転倒数 :
- 転倒数 :
- 転倒数 :
- 転倒数 :
よって である。
図による解釈
二項係数 は の格子状の道を左下から右上まで最短経路で進むときの場合の数でした。
-二項係数も格子状の道の経路を数えることで計算することができます。
マスの格子を左下から右上まで最短経路で進む際,下側のマスの個数が 個であるような経路の個数を とする。
と計算できる。
この方法で計算してみましょう。
- マスが 個
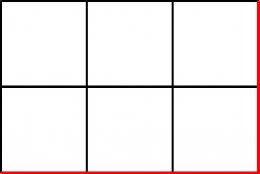
- マスが 個
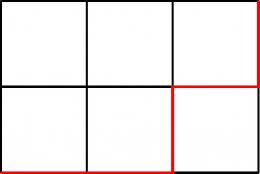
- マスが 個
- マスが 個
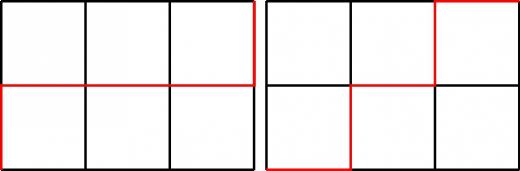
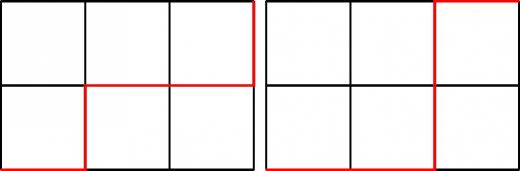
- マスが 個
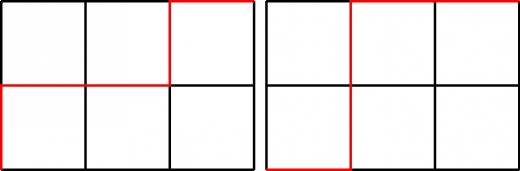
- マスが 個
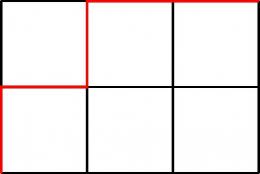
- マスが 個
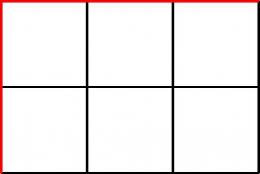
よって である。
証明
定義が一致することを確認しましょう。
の順列の転倒数を数える。前の定理からこの転倒数の母関数は である。
が配置されている箇所を に, が配置されている箇所を に取り換える。この と からなる数字の列の転倒数は であった。
こうしてできた順列の転倒数は次の3つの和である。
- と に置き換えた数列の転倒数
- 元の順列から から だけを取り出した際の転倒数
- 元の順列から から だけを取り出した際の転倒数
よって と表すことができる。
母関数の考え方から が従う。つまり が示された。
-二項定理の証明
-二項定理の証明
q-二項係数とq-二項定理 では,特殊な関数を用いて証明をしました。
この記事では組み合わせ論的に証明を試みましょう。
組み合わせ論による証明
の係数を求める。
のうちから 個を選んだものを とおく。このとき である。
ここで とおく。このとき で, である。
と マスの格子を左下から右上まで進む経路を次のように対応付ける。
- 列目で マス目まで上がる。
- 列目で マス目まで上がる。
- 列目で マス目まで上がる。
このとき,経路の下側のマスの個数は である。
ゆえに となるため, を得る。
であるため, の係数は である。
競技プログラミングでしばしば活用することがあるそうです。











