ヘルマート変換の意味・アフィン変換との関係

更新 2023/09/07

定義(ヘルマート変換)

$\begin{aligned}X&=ax-by+c\\ Y&=bx+ay+d\end{aligned}$

という式で $(x,y)$ を $(X,Y)$ にうつすような変換をヘルマート変換と言う。

ヘルマート変換は，測量などに用いられる変換です。

意味

ヘルマート変換の意味1 ヘルマート変換は，図形の形を保つ変換です。図形の大きさ・向き・位置は変わるかもしれませんが，形は変わりません。相似変換とも言います。

形が変わらないことは，以下の定理からわかります。

定理

ヘルマート変換は「平行移動」「回転」「拡大・縮小」という3種類の変換の合成で表される。

ヘルマート変換の意味2 ただし， $a=b=0$ の場合は除いて考えます。

証明

ヘルマート変換を行列で表すと $\begin{pmatrix}X\\Y\end{pmatrix}=\begin{pmatrix}a&-b\\b&a\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}+\begin{pmatrix}c\\d\end{pmatrix}$ である， $r=\sqrt{a^2+b^2}\neq 0$ とおく。ある $\theta$ が存在して $\begin{pmatrix}a&-b\\b&a\end{pmatrix}=r\begin{pmatrix}\frac{a}{r}&-\frac{b}{r}\\\frac{b}{r}&\frac{a}{r}\end{pmatrix}=r\begin{pmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{pmatrix}$ となる。つまり，ヘルマート変換は「 $\theta$ 回転」と「 $r$ 倍の拡大」と「 $(c,d)$ の平行移動」という3つの変換の合成で表される。

アフィン変換・線形変換との関係

中学数学で習う比例の多変数バージョンが線形変換(1次変換)です。2変数の場合， $\begin{aligned}X&=ax+by\\ Y&=cx+dy\end{aligned}$ と書けます。
→一次変換の意味と重要な5つの例（折り返し・回転・対称移動）
平行移動も考えると1次関数になりますが，その多変数バージョンがアフィン変換です。2変数の場合， $\begin{aligned}X&=ax+by+c\\ Y&=dx+ey+f\end{aligned}$ と書けます。
上記のアフィン変換の式で，特に $a=e$ ， $b=-d$ を満たすものがヘルマート変換です。

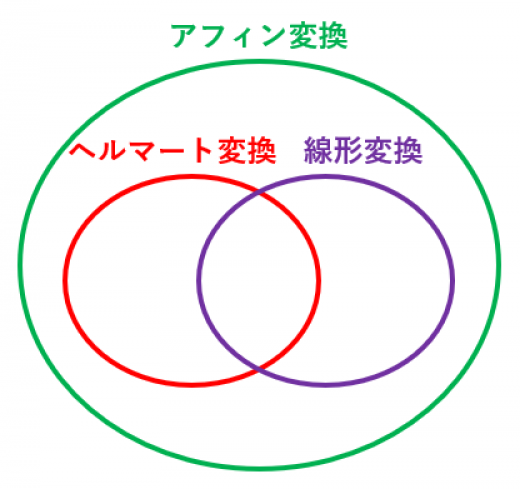
各変換の構成要素

ヘルマート変換は「平行移動」「回転」「拡大・縮小」の3つの合成で表されます。
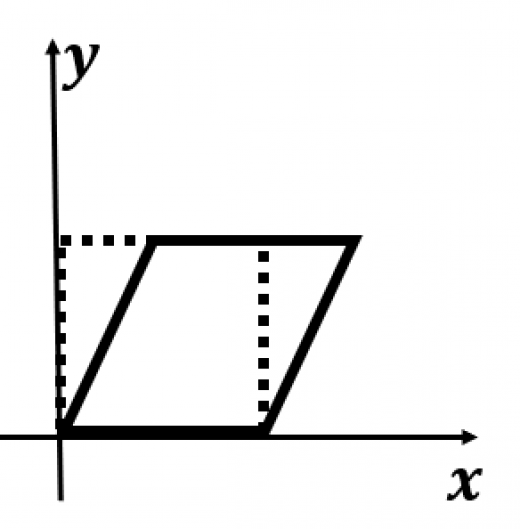
アフィン変換は「平行移動」「回転」「拡大・縮小」に加えて「せん断（スキュー）」という4つの基本的な変換の合成で表されます。「せん断」は図のように正方形(点線)を平行四辺形(実線)に歪めるような変換です。
線形変換は「回転」「拡大・縮小」「せん断」の3つの合成で表されます。平行移動は許容しません。

なお，アフィン変換や線形変換は2次元だけでなく一般の $n$ 次元でも考えることができますが，3次元以上の場合のヘルマート変換は考えないと思います（少なくとも私は見たことがありません）。

ヘルマート変換と言うとかっこいいですが，ただの相似変換です。ただし，行列 $A$ に対して $P^{-1}AP$ という変換を相似変換と言うこともあるのでややこしいです。

この記事の監修者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！