ローレンツ曲線とジニ係数~均等度合いを示す指標
ジニ係数とは,データの不平等さの具合を見る指標である。
以上 以下の実数をとり, に近ければ近いほど,分布が均一であることを示す。
この記事では,経済学や社会学で用いられる**ジニ係数(ジニ指数)**の定義と求め方を解説します。
収入の例
収入の例
例えば次のデータを考えましょう(あらかじめデータは下から並べてあります)。 さんから さんまで25人分の月収を表しています。
月収の総和は 万です。このデータから,ローレンツ曲線と呼ばれる曲線を描いていきます。
小さい順から見ていって,
- 最初の1人(全体の4%)で月収の総和のうち1.5%(1000万のうちの15万)を占める
→をプロットする - 最初の2人(全体の8%)で月収の総和のうち3.2%(1000万のうちの32万)を占める
→をプロットする
というような折れ線グラフがローレンツ曲線です。
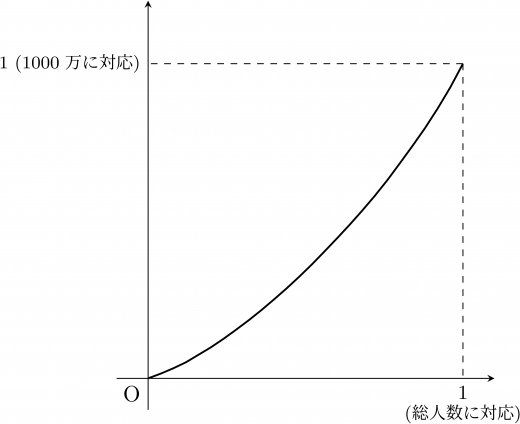
※ なめらかに見えますが,解像度の問題です。細かく見ると折れ線のグラフとなります。
ジニ係数とは,「」と「ローレンツ曲線」で囲まれた部分の面積の2倍のこと。
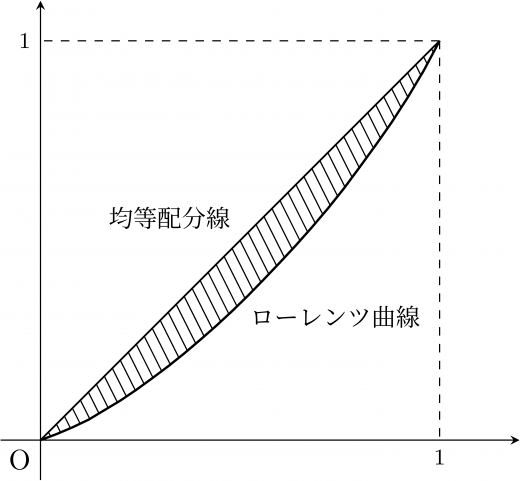
※ のことを均等配分線と言います。
収入の例でジニ係数を計算してみましょう。次のように,ローレンツ曲線の下側部分を台形に分けて考えます。
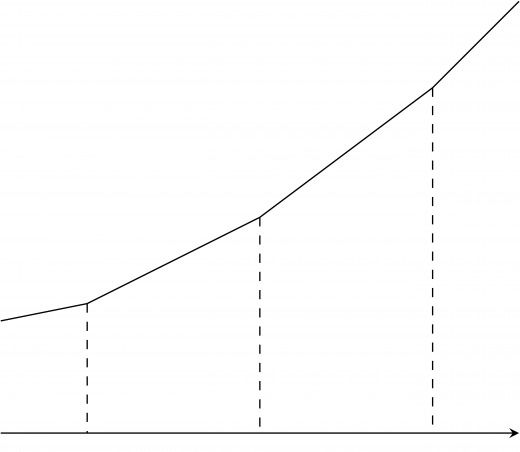
これらの面積を足していけば全体の面積が分かります。 を計算すると,おおよそ となります。ゆえにジニ係数はおおよそ となります。
ジニ係数の性質
ジニ係数の性質
もしデータがどの階級にも集中することなく分布しているとしたら,ローレンツ曲線は次のように直線状になります。
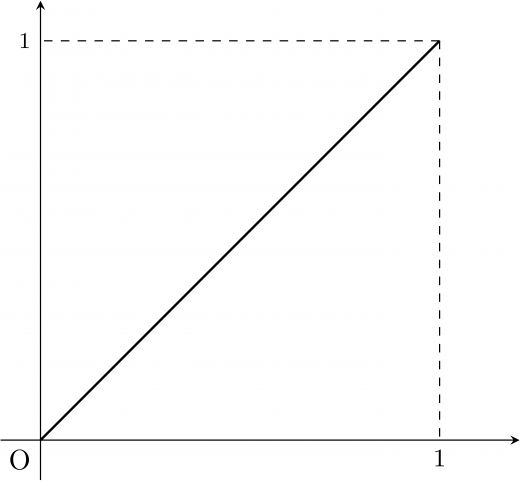
この直線 のことを均等配分線といいます。完全に平等な場合,ローレンツ曲線と均等配分線は一致します。すなわち,面積は0なのでジニ係数は0になります。
データに偏りがある場合,ローレンツ曲線は下に凹みます。
日本・世界のジニ係数
日本・世界のジニ係数
ジニ係数は,所得に対して計算され,所得の偏りの指標として用いられることが多いです。
日本のジニ係数
日本におけるジニ係数を見ていきましょう。
数年の一度,厚生労働省が所得再分配調査を行っており,同時にジニ係数の公開も行われています。→ 所得再分配調査(厚生労働省)
これによると,令和3年(2021年)の純粋な収入に対するジニ係数は でした。税金などを通した社会保障の結果,ジニ係数は まで改善されているようです。 一般に,ジニ係数が を超えると格差が大きいとされるため,社会保障を通した再分配が非常に意味のあるものだと分かりますね。
厚生労働省以外にもジニ係数を計算している機関は国内外問わず存在します。機関によって,サンプルの選び方が一部変わりますので,ジニ係数も軽微に変わります。しかし,どの集計においても日本のジニ係数は 台となっています。
世界のジニ係数
OECDが各国のジニ係数を集計しています。→ OECD:Income distribution database
この集計では,2021年の日本のジニ係数が となっています。同年のアメリカは と日本より若干格差が大きいようです。
OECDの調査対象国でジニ係数が大きい国としてはコスタリカ(2021年 )や南アフリカ(2017年 )などがあります。
より厳密な説明
より厳密な説明
ここまで,例をもとに大雑把な説明をしてきました。以下では,もう少し正確に各用語を述べておきます。
度数
-
累積相対度数とは,値が低い方から順にデータを並べたとき,全体のうち何%がそこまでに含まれているかを表します。
-
累積配分比率とは,値が低い方から順に並べたとき,サンプルが全体の値のうち何%を得ているかを表します。
-
例えば,「収入が下位30%の人の収入の合計が,全体の収入の10%である」場合,「累積相対度数 における累積配分比率は 」です。
ローレンツ曲線
ローレンツ曲線とは,与えられたデータについて
- 横軸:累積相対度数
- 縦軸:累積配分比率
をプロットしたグラフである。
ローレンツ曲線は,与えられたデータに対して,下から %以下が全体のうち何%か表した曲線です。
ジニ係数
ジニ係数とは,均等配分線とローレンツ曲線で囲まれた部分の面積の2倍である。
同値な言い換えとして均等配分線の右下部分の面積()と 均等配分線とローレンツ曲線で囲まれた部分の面積の比としてもよい。
なお,収入の例を考えましたが,収入以外のデータでもジニ係数は同様に計算できます。
友人にお小遣いやバイト代を聞いてジニ係数を計算してみるのも面白いでしょう。










