半正多面体と準正多面体
更新
- 半正多面体と準正多面体の意味を説明します。
- 半正多面体全13種類を紹介します。
- 13種類しかないことを証明します。
半正多面体とは
半正多面体とは
対称性の高い多面体を考えます。
- 正多面体(regular polyhedron)とは,「1種類の正多角形のみからなる」「すべての頂点まわりが合同な」「凸な」多面体です。
正4面体,正6面体,正8面体,正12面体,正20面体の5つのみです。 →正多面体が5種類しかないことの2通りの証明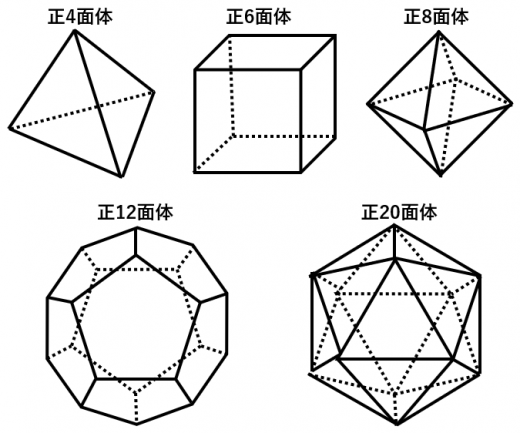
次に,使う正多角形の種類を2種類以上でもOKとしてみましょう。
- 準正多面体(quasi-regular polyhedron)とは,「正多角形のみからなる」「すべての頂点まわりが合同な」「すべての辺まわりが合同な」「凸な」多面体です。ただし,正多面体は除きます。準正多面体は,後述の立方八面体と二十・十二面体の2種類のみです。
さらに,「辺まわりが合同」を諦めましょう。
- 半正多面体(semi-regular polyhedron, アルキメデスの立体)とは,「正多角形のみからなる」「すべての頂点まわりが合同な」「凸な」多面体です。ただし,正多面体と対称性が低い特殊な立体(角柱・反角柱・ミラーの立体)は除きます。半正多面体は13種類あります。
さらに,「凸」も諦めましょう。
- 一様多面体とは,「正多角形のみからなる」「すべての頂点まわりが合同な」多面体です。ただし,角柱・反角柱・ミラーの立体は除きます。一様多面体は75種類あります。
なお,この記事における,2~4の定義および図は Wikipedia のものを引用・加工しています。
半正多面体一覧
半正多面体一覧
正多面体の頂点を「少し」切り落とした5種
正多面体の角をちょっと切り落とすと,半正多面体になります。
例えば,正4面体の角4つを切り落とすと切頂4面体という立体になります。
 ただし,切り落としてできる辺と,「もとの正多面体の辺で残る部分」の長さが同じになるように切り落とします。
切頂4面体は「4面体を切り落とした多面体」です。面の数は4つではなく8つです。
ただし,切り落としてできる辺と,「もとの正多面体の辺で残る部分」の長さが同じになるように切り落とします。
切頂4面体は「4面体を切り落とした多面体」です。面の数は4つではなく8つです。
正多面体は5つあるので,このようにして半正多面体が5つ得られます。
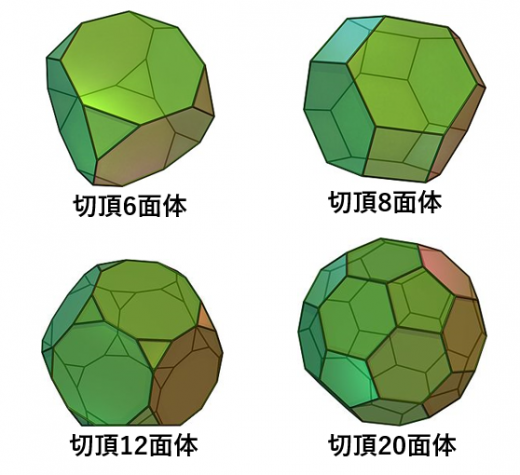 切頂20面体はサッカーボールです!
切頂20面体はサッカーボールです!
正多面体の頂点を「辺の中央まで」切り落とした2種
正6面体(立方体)の8つの角を辺の中央まで切り落とすと半正多面体が得られます。
 これを立方8面体と言います。実は,正8面体の角を中央まで切り落としたものも同じ立方8面体になります。「立方体」と「正8面体」のハーフということで「立方8面体」です。
これを立方8面体と言います。実は,正8面体の角を中央まで切り落としたものも同じ立方8面体になります。「立方体」と「正8面体」のハーフということで「立方8面体」です。
同様に,「正12面体の角を辺の中央まで切り落とす」あるいは「正20面体の角を辺の中央まで切り落とす」と二十・十二面体という半正多面体が得られます。
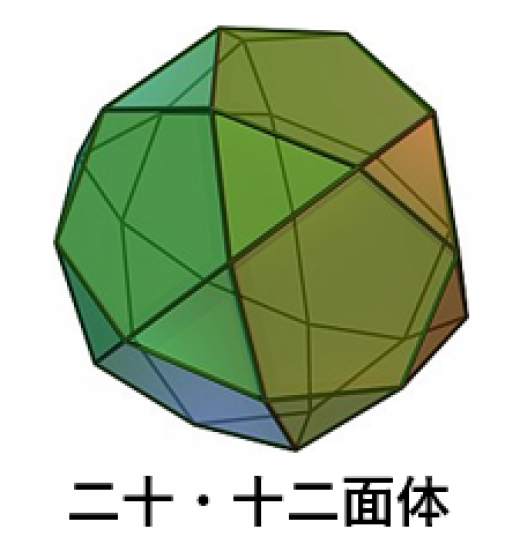
この2種はどの辺まわりも合同なので,準正多面体です。
ちなみに,正4面体の各角を辺の中央まで切り落とすと正8面体になります。
正多面体2種類と「斜めの正方形」でできる2種
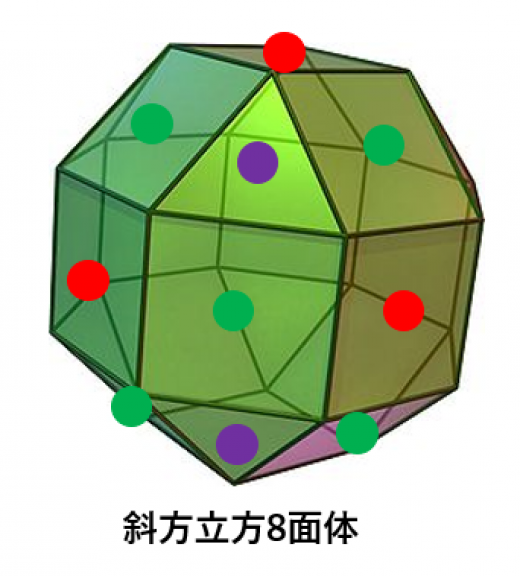
斜方立方8面体という半正多面体があります。これは,
- 斜方(斜めの正方形12枚)
- 立方体(の正方形6枚をひきはがしたもの)
- 正8面体(の正三角形8枚をひきはがしたもの)
からなります。
同様に,斜方二十・十二面体という半正多面体もあり,これは
- 斜方(斜めの正方形30枚)
- 正20面体(の正三角形20枚をひきはがしたもの)
- 正12面体(の正五角形12枚をひきはがしたもの)
からなります。

その他4種
残りの4つは図を見てください。
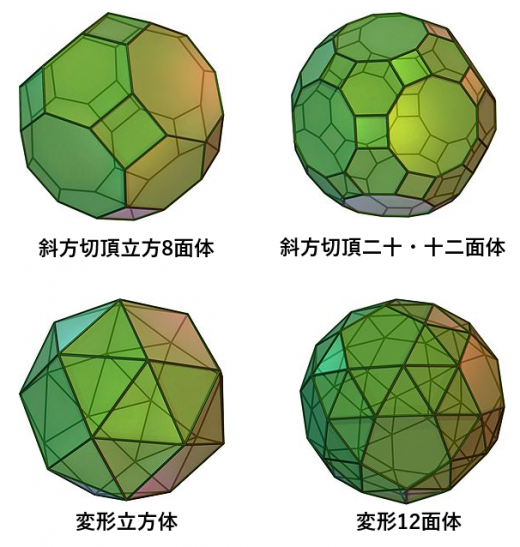
- 斜方切頂立方8面体は,立方8面体の各頂点を切った形に似ています。
- 斜方切頂二十・十二面体は,二十・十二面体の各頂点を切った形に似ています。
- 変形立方体は,立方体の正方形6枚をひきはがして間に三角形を入れたらできます。
- 変形12面体は,正12面体の正5角形12枚をひきはがして間に三角形を入れたらできます。
13種類しかないことの証明
13種類しかないことの証明
半正多面体は上記の13通りのみ。
半正多面体では頂点まわりが合同なので,1つの頂点のまわりにある正 角形たちの並び で表せる。
例えば,立方8面体は と表せる。

-
正 角形の1つの内角は 度であり,1つの頂点に集まる角度の和は 未満なので, となる。これを整理すると, となる。
-
1種類だと正多面体になるので, は2種類以上から構成される。
-
だと,1つの頂点に集まる角度が 以上になるので凸多面体にならない。 でも多面体にならない。
以上の条件を満たす をすべて列挙する。
-
のとき
四角形以上を2つ以上使うと集まる角度が 以上になる。よって,4つは三角形であり, の2種類。作ってみると,変形立方体と変形12面体になる。 -
のとき
全部四角形以上だと,集まる角度が 以上になるので,三角形が1つはある。また,1つの三角形の3頂点まわりを全部合同にするには同じ正多角形を つ以上使う必要がある(図で が相異なるとき, と仮定できて,3頂点まわりを全部合同にするには が必要だが をどのように決めても3頂点まわりを全部合同にはできない)。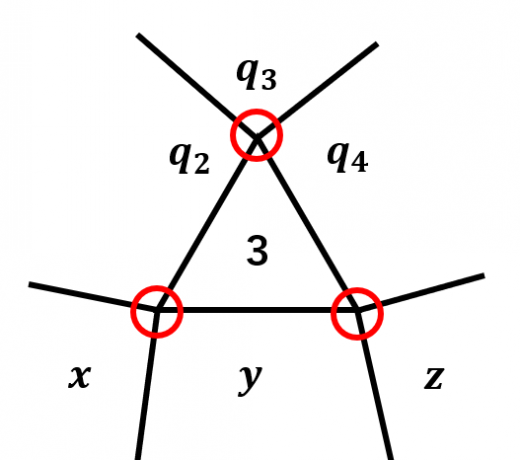 つまり, とおける。紫文字の制約は,
となる。この式は,
つまり, とおける。紫文字の制約は,
となる。この式は,- なら簡単に全列挙できる。具体的には,,,, の4種類で,それぞれ立方8面体,二十・十二面体,斜方立方8面体(※),斜方二十・十二面体ができる。
- とすれば は何でもOK。 という無数の解ができるが,これは反角柱なので例外(半正多面体ではない)。

-
で奇数角形を使う場合
を奇数とする。1つの 角形の頂点まわりを全部合同にするには が必要。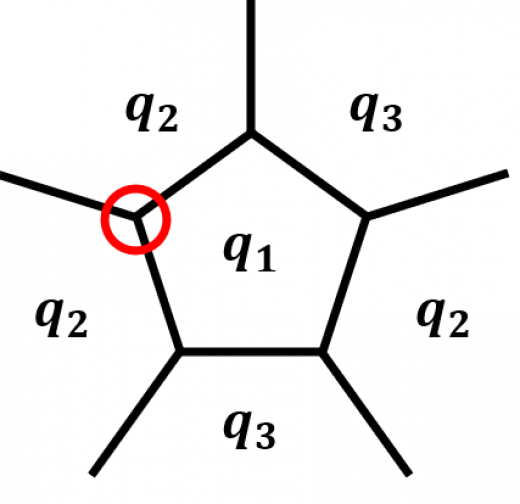
- の場合, だと正5角柱で例外。 だと切頂20面体
- の場合, だと正3角柱で例外。 だと切頂4面体, だと切頂6面体, だと切頂12面体,
-
で奇数角形を使わない場合
全部6角形以上だと,集まる角度が 以上になるので,四角形を1つは使う必要がある。 とする。- のとき, は何でもOK。無限個解ができるが,これは角柱なので例外。
- のとき, だと切頂8面体, だと斜方切頂立方8面体, だと斜方切頂二十・十二面体
- も も 以上だと集まる角度が 以上になる。
※ からは斜方立方8面体だけでなく,上側と下側がずれている「ミラーの立体」というものもできます。これは例外扱いで,半正多面体とは考えません。

1000記事目なので気合入れて書きました。これからもよろしくお願いします!











