行列木定理とCayleyの定理
更新
無向グラフ に対して, の全域木の個数は, のラプラシアン行列の任意の余因子と等しい。
行列木定理の意味と証明,そして応用例として Cayley の定理の証明を紹介します。
行列木定理の意味
行列木定理の意味
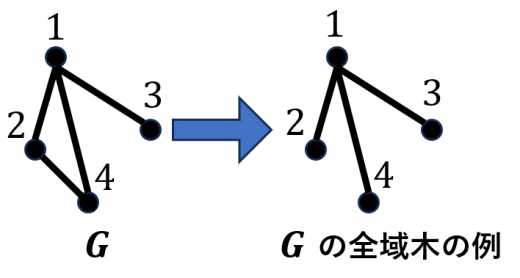
の全域木とは, のすべての頂点を含む木(閉路を含まない部分グラフ)です。→グラフ理論の基礎
のラプラシアンとは,各行,列がそれぞれ の頂点に対応しており,対角成分にはその頂点の次数,非対角成分については枝がある部分に ,無い部分に を格納した正方行列です。→隣接行列,接続行列,ラプラシアン行列
例えば,上図の のラプラシアンは です。この 余因子は, です,実は の全域木の個数も です。 余因子や 余因子など,他の余因子もすべて になります!
行列木定理の証明
行列木定理の証明
以下の2つにわけて,証明します。
- ラプラシアン行列の 余因子 は によらず一定
- は の全域木の個数と同じ
を示す。他の余因子が等しいことも同様に示せる。
わかりやすさのために の場合で示す。一般の でも同様。
である。ただし, は頂点 の次数である。1列目に1列目以外の各列を加えることで, となる(もとのラプラシアン行列で各行の和が であることを使った) これはまさに符号まで含めて である。
次に2です。行列式に関するビネ・コーシーの定理を使います。少し難しいですがとてもおもしろいです。
の点枝接続行列を とする。ただし, なる頂点 間に枝があるとき, 側の要素は , 側の要素は とする。
 例えば,図の例だと
である。行数= の頂点数,列数= の枝数となる行列である。例えば の3行目より,頂点1と4を結ぶ枝()があることがわかる。 とラプラシアン の定義より, となる。よって, の1行目を除いた行列を とすると,
となる。右辺にビネ・コーシーの定理を使うと,
となる。ただし, は枝のラベル から 個( は の頂点数)選んだ集合全体を動く。
例えば,図の例だと
である。行数= の頂点数,列数= の枝数となる行列である。例えば の3行目より,頂点1と4を結ぶ枝()があることがわかる。 とラプラシアン の定義より, となる。よって, の1行目を除いた行列を とすると,
となる。右辺にビネ・コーシーの定理を使うと,
となる。ただし, は枝のラベル から 個( は の頂点数)選んだ集合全体を動く。
つまり, により の枝が 個決まるが,
- これらが全域木をなさない,つまり閉路を含むとき である。 実際,頂点1を含まない閉路があるときは, のように,行和が ベクトルになるので行列式が 。頂点1を含む閉路があるときは,頂点1以外に孤立点があり, のその行はすべて なので行列式は
- これらが全域木をなすとき, である。 実際, などとなるが,置換による行列式の定義を考えたとき, を選ばない置換がただ1つになる。もう少し詳しく言うと「木は次数1の頂点を2つ以上含む(頂点1以外で次数1のものが存在する)」ことと「木から次数1の頂点を1つ除いても木のまま」であることから, を選ばない置換を構成しようとするとただ1つになる。
よって, は の全域木の個数と等しい。
Cayley の定理
Cayley の定理
個の(ラベル付き)頂点を持つ木の個数は
 例えば のときは図のように 通りです。たしかに になっています。
例えば のときは図のように 通りです。たしかに になっています。
行列木定理を使って証明できます。
わかりやすさのために で計算する。一般の でも同様。
頂点数 の完全グラフに行列木定理を使うと
1行目以外の各行から1行目を引くことで,
1列目以外の各列を1列目に加えることで,
上三角行列の行列式は対角成分の積なので と等しい。
行列木定理を使わず直接 Cayley の定理を証明する方法もたくさんあります。
参考文献:Kirchhoff’s theorem
大学院の授業の演習問題で Cayley の定理の証明が出題されて,全く歯が立たなかった記憶があります。











