第5問
実数 y に対して tanx=y を満たす実数 −2π<x<2π を θ(y) によってあらわす。
例えば,θ(1)=4π,θ(0)=0 である。
(1) θ(3) を求めよ。
(2) m,n を m>n≧2 となる整数とする。このとき方程式
θ(m1)+θ(n1)=4π
を満たす (m,n) を求めよ。
(3) m,n を 2 以上の整数とする。このとき方程式
2θ(m1)−θ(n1)=4π
を満たす (m,n) を求めよ。
(4) x を有理数,n を 2 以上の整数とする。このとき方程式
2θ(x)−θ(n1)=4π
を満たす (x,n) に現れる n を小さい順に3つ求めよ。
なお,問題を解く上で次の事実を用いてよい。
- 整数の数列 {xk},{yk} を (1+2)k=xk+yk2 により定義したとき,x2−2y2=±1 の整数解は (xk,yk) によって得られる。また (xk,yk) に現れる数字以外に解となる数は存在しない。
第5問は三角関数の逆関数,特に tan の逆関数 arctan に関する問題です。arctan は高校で習いませんが,問題文中のように定義されて入試問題に登場することがしばしばあります。
第5問 (1)
tan3π=3 より θ(3)=3π である。
この問題は (2) から三角関数の皮をかぶった整数問題に変わります。ポイントは tan(θ(x))=x となることです。
第5問 (2)
与式から
tan(θ(m1)+θ(n1))=tan(θ(m1))+tan(θ(n1))1−tan(θ(m1))tan(θ(n1))=m1+n11−mn1=m+nmn−1=1
である。すなわち
mn−m−n=1
が成立する。これは
(m−1)(n−1)=2m=3,n=2
と計算できる。こうして解は (m,n)=(3,2) である。
このようにして
arctan21+arctan31=4π
という式が得られます。
実はこの式は次のように幾何的に求めることができます。
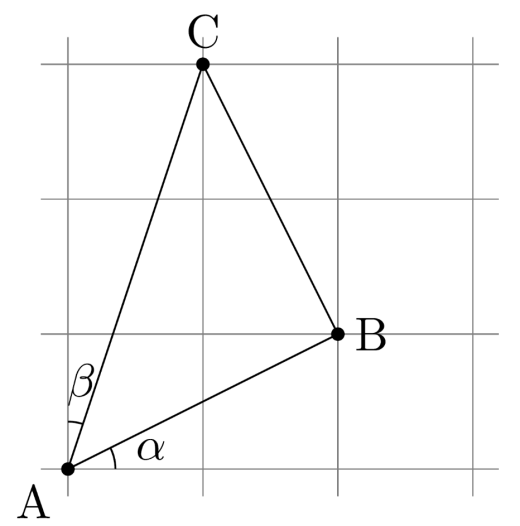
上図の1めもりを 1 とします。このとき α=arctan21,β=arctan31 です。また AB=5,CA=10,BC=5 です。これら辺の長さの比を見ると,1:2:1 です。よって三角形 ABC は直角二等辺三角形で,∠BAC=4π だとわかります。
点 A があるカドに注目すると α+β+4π=2π となることがわかります。こうして α+β=4π が得られます。
さて次の問題はより状況が複雑になります。二倍角の公式などを用いて θ がない式を求めましょう。
第5問 (3)
与式を移項すると,
θ(n1)=2θ(m1)−4π
となる。
n1=tan(θ(n1))=tan(2θ(m1)−4π)=1+tan(2θ(m1))tan4πtan(2θ(m1))−tan4π=1+m2−12mm2−12m−1=m2+2m−1−m2+2m+1
と計算される。なお
tan(2θ(m1))=1−tan2{θ(m1)}2tan{θ(m1)}=1−m212⋅m1=m2−12m
である。
m2+2m−1 と −m2+2m+1 の最大公約数を d とすると,
m2+2m−1=nd−m2+2m+1=d
と表される。これより 4m=(1+n)d が得られる。
今 d=1 が m の約数であると仮定すると,m=ld (l∈Z)で表されるが,与式を変形すると 1=m2−2m+d=(l2−2l+1)d となる。l2−2l+1,d は整数であったため,d=1 となるが,これは d=1 に反する。よって d は m の約数とはならない。
したがって d=±1,±2,±4 である。
−(m−1)2+2=d と変形して,それぞれ計算すると整数解として (d,m)=(1,2),(2,1),(−2,3) が得られる。m<2 より2つめは不適である。(d,m)=(−2,3) のとき,n=−7 となるが,n<2 より不適である。
こうして m=2 であり,このとき n=7 と計算される。こうして
2θ(21)−θ(71)=4π
が得られる。
n1=m2+2m−1−m2+2m+1
から即座に −m2+2m+1=1 としたいですが,そうはいきません。事実,条件 n≦2 を満たさないものの −m2+2m+1=2 でも整数解があります。
最後の問題はさらに一般的な状況での解を計算するものとなります。事実として与えられているペル方程式をうまく利用しましょう。
第5問 (4)
前の問題同様に式変形すると
n1=tan(θ(n1))=tan(2θ(x)−4π)=1+tan(2θ(x))tan4πtan(2θ(x))−tan4π=1+1−x22x1−x22x−1=−x2+2x+1x2+2x−1
となる。x=qp とおく。なお p,q は互いに素な2整数とする。変形して
n1=−p2+2pq+q2p2+2pq−q2
が得られる。
−p2+2pq+q2 と p2+2pq−q2 の最大公約数を d とすると,
−p2+2pq+q2p2+2pq−q2=nd=d
となる。辺々足すことで 4pq=(n+1)d が成立する。
d が 4 と互いに素で p を割り切ると仮定すると,q2=d−p2−2pq の右辺は d の倍数となり,q も d の倍数となる。これは p,q が互いに素であることに反する。q を割り切るときも同様に考えると,あり得ないことがわかる。よって d=±1,±2,±4 となる。
p2+2pq−q2=p2+2pq+q2−2q2=(p+q)2−2q2
である。ここで p+q=X,q=Y とおく。
- d=±1 のとき
解くべき方程式は X2−2Y2=±1 となる。分母は
−p2+2pq+q2=−(p2+2pq−q2)+4pq=4pq∓1=4(X−Y)Y∓1
と得られる。
事実から X2−2Y2=±1 の解は,(1+2)n=xN+yN2 なる (xn,yn) で得られる。
xN+1+yN+12=(1+2)N+1=(1+2)(1+2)N=(1+2)(xN+yN2)=(xN+2yN)+(xN+yN)2
より,
{xN+1=xN+2yNyN+1=xN+yN
である。帰納的に xN,yN が単調に増加することがわかる。
さて (X,Y)=(xN,yN) としたとき,
n=4(xN−yN)yN+(−1)N−1=4yN−1yN+(−1)N−1
となる。yN は単調に増加することから n も N に応じて単調に増加する。よって N=4 から順に計算すれば良いことがわかる。
N=1 のときは yN−1=y0=0 より n=1 となるため,n≦2 に反する。N=2,3,4 をそれぞれ計算すると,n=7,41,239 となる。こうして 1 のとき,条件を満たす n は小さい順に 7,41,239 である。
- d=±2 のとき
解くべき方程式は X2−2Y2=±2 である。X2=2Y2∓2 より X2 は 2 の倍数である。よって X も 2 の倍数となる。
X=2X′ とおくと方程式は 4X′2−2Y2=±2 となる。辺々を −2 で割ると,Y2−2X′2=∓1 が得られる。
(Y,X′)=(xN,yN) とおく。p=X−Y=2X′−Y である。このとき
n=2−p2+2pq+q2=2−(p2+2pq−q2)+4pq=2pq(−1)N=2(2yN−xN)xN+(−1)N=2xN−1xN+(−1)N
である。1 同様に考えることで n は N に応じて単調に増加する。N=1 のときは 1 同様に不適である。N=2,3,4 を順に計算すると n=7,41,239 である。
こうして 2 のときも条件を満たす n は小さい順に 7,41,239 である。
- d=±4 のとき
解くべき方程式は X2−2Y2=±4 である。X2=2Y2∓4 より X2 は 2 の倍数である。よって X も 2 の倍数となる。X=2X′ とおくと方程式は 4X′2−2Y2=±4 となる。辺々を −2 で割ると,Y2−2X′2=∓2 が得られる。同様に考えると Y が 2 の倍数となる。p=X−Y,q=Y となることから,X,Y の公約数が 2 であることは p,q が互いに素であることと矛盾する。
以上より求めるべき解答として n=7,41,239 が得られる。
問題の解答を見て察しの良い方は n の数字自体は d=±1 のときと d=±2 のときで同じものが出ると思うでしょう。実際にそれは成立します。このように計算されます。
4yN−1yN+(−1)N−1=4(xN−yN)yN+(−1)N−1=4xNyN−4yN2+(−1)N−1=4xNyN−2(xN2+(−1)N−1)+(−1)N−1=4xNyN−2xN2−2(−1)N−1+(−1)N−1=2(2yN−xN)xN+(−1)N=2xN−1xN+(−1)N
さてこの問題には続きがあります。
追加問題
x を有理数,n を 2 以上の整数とする。このとき方程式
4θ(x)−θ(n1)=4π
を満たす最小の n を求めよ。
追加問題
θ(z)=2θ(x)
が成立するとする。このとき
tanθ(z)z==tan2θ(x)=1−tan2θ(x)2tanθ(x)=1−x22x
という関係式が得られる。
よって
4θ(x)−θ(n1)=4π
を満たす有理数 x が与えられたとき,z=1−x22x によって有理数 z を取ると
2θ(z)−θ(n1)=4π
が成立する。
以上より
2f(z)−f(n1)=4π
の解であって,z=1−x22x の解 x が有理数となるものを探せばよい。実際に計算すると d=±1,n=4 のとき z=125 が x=51 を与える。
こうして n=239 である。
この問題によって
4arctan51−arctan2391=4π
という関係式が得られます。これは円周率の求め方でも登場しているマチンの公式というものです。
ペル方程式が無数に解を持つことにより,(4) の形をした arctan の公式は,無数に存在することがわかります。では追加問題のような
4arctanx−arctann1=4π
を満たす式は他にあるのでしょうか。
2f(z)−f(n1)=4π
の解であって,z=1−x22x の解 x が有理数となるものが他にあるのかという問いになります。
x を z で表すと x=−1±1+z2 となります。ここで互いに素な2整数 p,q により z=qp とおくと p2+q2 が平方数になれば良いとわかります。この平方数を r2 とでもおきましょうか。
さて (4) の解答を思い出すと
−p2+2pq+q2p2+2pq−q2=nd=d
だったのでした。辺々を二乗して足します。左辺は
(−p2+2pq+q2)2+(p2+2pq−q2)2=2p4+4p2q2+2q4=2(p2+q2)2=2r4
となり,右辺は (n2+1)d2 となります。
d=2 のときは 2r4=4+4n2 となります。偶奇に注目すると r が偶数であることが従い,整数 r′ により r=2r′ と置き換えることができます。すると 8r′4=1+n2 が得られますが,右辺を 8 で割った余りが 0 になることがないため,この式の整数解はありません。
d=1 のとき,2r4=n2+1 という方程式が得られます。これはリュングレンの方程式と呼ばれていて,解は (r,n)=(1,1),(239,13) だけであることが証明されています。(r,n)=(1,1) のときは z=0 となってしまい求めていたものとはなりません。もう一方の解にマチンの公式が対応しています。
こうして問いの答えは「マチンの公式しか存在しない」ということになります。大変興味深いですね。
なお,リュングレンの方程式を解くには代数的整数論の知識が必要なのでここでは触れません。興味がある人は勉強してみましょう。
また意欲のある方は 4 の部分を 3 や 5 など他の整数に変えて考えてみましょう。 3,5 のケースは 2 のときと同じ方法で簡単に解くことができます。






