入試数学コンテスト第1回第1問解答解説

$a=1$ の時, 与式は $$\cos^2\theta + \sin \theta + b-1 = 0 \\ \iff -\sin^2 \theta + \sin \theta + b = 0$$

である。

$\sin \theta = k \; (0 \leqq \theta \leqq \pi)$ と置くと, 方程式は $$k^2 - k = b \tag{1}$$ と変形される。

この時, $\theta$ の方程式 $\sin \theta = k$ について, 解の個数は

1. $0 \leqq k \lt 1$ のとき, 異なる2つの解を持つ。
2. $k = 1$ のとき, ただ1つの解( $\theta = \dfrac{\pi}{2}$ )を持つ。
3. $k \lt 0,1 \lt k$ のとき, 解なし。

である。

方程式（1）は $k$ の二次方程式であるから, その解は高々2つである。

方程式（1）が $0 \leqq k < 1$ の範囲に異なる2つの解を持てば, それぞれの $k$ に対して2つの相異なる $\theta$ が対応し, かつ $k$ の値が異なることから4つの $\theta$ は互いに相異なる。

それ以外の場合は 解 $\theta$ の数は3つ以下である。

以上から, 題意のための必要十分条件は「方程式（1）が $0 \leqq k < 1$ の範囲に異なる2つの解を持つ」ことである

二次関数 $y = k^2 - k \; (0 \leqq k < 1)$ と直線 $y = b$ の交点の数が（異なる）2つになるような $b$ の値の範囲を考えればよく, これを満たす $b$ の値の範囲は

$$-\dfrac{1}{4} < b < 0$$

である。

与式は $$\cos^2\theta + a\sin \theta + b-1 = 0 \\ \iff \sin^2 \theta - a\sin \theta - b = 0$$ である。

(1)と同様に $\sin \theta = k \; (0 \leqq \theta \leqq \dfrac{3}{2}\pi)$ と置くと, 方程式は $$k^2 - ak - b= 0$$ と変形される。

この時, $\theta$ の方程式 $\sin \theta = k$ について, 解の個数は

1. $0 \leqq k \lt 1$ のとき, 異なる2つの解を持つ。
2. $-1 \leqq k < 0,k = 1$ のとき, ただ1つの解を持つ。
3. $k \lt -1,1 < k$ のとき, 解なし。

である。

(1)と同様に, $0 \leqq \theta \leqq \dfrac{3}{2}\pi$ のとき, ある $\theta$ を取りうる $k$ の値はただ一つに定まることに注意する。

題意のための必要十分条件は, $k$ の方程式 $k^2-ak-b=0$ が

• 条件1. $0 \leqq k \lt 1$ の範囲に少なくとも1つ解を持つ。

• 条件2. $-1 \leqq k \lt 0$ の範囲に異なる2つの解を持つ。

• 条件3. $-1 \leqq k \lt 0$ の範囲に1つの解をもち, かつ $k=1$ も解である。

のいずれかの条件を満たすことである。

$f(k) = k^2-ak-b$ とおき, それぞれの場合について考える。

• 条件1のとき

① $f(0)f(1) \lt 0$ のとき, すなわち $b(a+b-1) < 0$ のとき, 常に題意を満たす。

$$\begin{cases} b < 0 \\ b > -a + 1 \end{cases} \, \text{または} \, \begin{cases} b > 0 \\ b < -a + 1 \end{cases} \tag{\text{A}}$$

② $f(0) = 0$ のとき, すなわち $b=0$ のとき, 常に題意を満たす。

$$b = 0 \tag{\text{B}}$$

③ $f(1) = 0$ のとき, すなわち $a+b-1=0$ のとき,

$$f(k) = (k-1)(k+1-a)$$ となるので $f(k) = 0$ のもう一つの解は $k = a-1$ である。

したがって $0 \leqq a-1 \lt 1 \iff 1 \leqq a < 2$ のとき題意を満たす。

$$\begin{cases} b = -a + 1 \\ 1 \leqq a < 2 \end{cases} \tag{\text{C}}$$

④ $$\begin{cases} \text{判別式} \quad D = a^2 + 4b \geqq 0 \\ \text{軸} \quad 0 \lt \dfrac{a}{2} < 1 \\ f(0) > 0\\ f(1) > 0 \end{cases}$$

のとき, すなわち

$$\begin{cases} b \geqq -\dfrac{1}{4}a^2\\ 0 \lt a \lt 2\\ b \lt 0\\ b \lt -a + 1 \end{cases} \tag{\text{D}}$$

のとき題意を満たす。

• 条件2のとき

$$\begin{cases} \text{判別式} \quad D = a^2 + 4b > 0 \\ \text{軸} \quad -1 \lt \dfrac{a}{2} < 0 \\ f(-1) \geqq 0\\ f(0) > 0 \end{cases}$$

のとき, すなわち

$$\begin{cases} b \gt -\dfrac{1}{4}a^2\\ -2 \lt a \lt 0\\ b \leqq a + 1\\ b \lt 0 \end{cases} \tag{\text{E}}$$

のとき題意を満たす。

• 条件3のとき

$k = 1$ を解に持つので, $f(1) = 0$ すなわち $b = -a + 1$ である。

この時 $f(k) = (k-1)(k+1-a)$ となるので, $-1 \leqq a-1 \lt 0 \iff 0 \leqq a \lt 1$ のとき題意を満たす。

$$\begin{cases} b = -a + 1 \\ 0 \leqq a < 1 \end{cases} \tag{\text{F}}$$

以上、$\text{(A)〜(F)}$ をまとめて $ab$ 平面に図示すると下図を得る(境界線は赤線部のみ含む)。

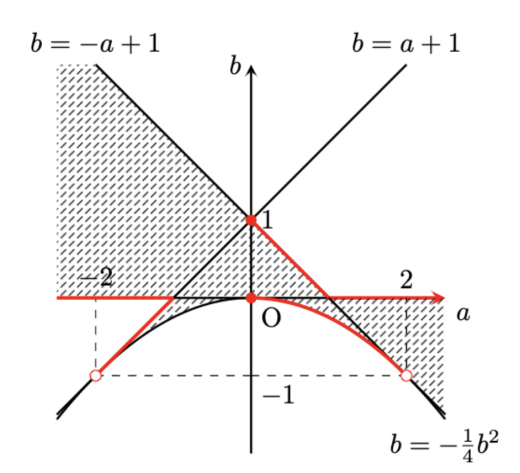
続いて $ab$ の範囲について議論を行う。

1. $ab = 0$ のとき

$b=0$ が上図の領域内に含まれるため $ab = 0$ は取ることができる。

2. $ab \neq 0$ のとき

$ab = t \; (t \neq 0)$ と置くと, $b = \dfrac{t}{a}$ は $ab$ 平面上で反比例のグラフになる。

「$ab = t$ という値を取る $\iff$ $b = \dfrac{t}{a}$ が上図の領域と共有点を持つ」

と言い換えることができる。

まず $t < 0$ の場合を考える。

$t < 0$ のときに反比例のグラフは第二象限と第四象限に存在するが, 図を見れば任意の $t \; (< 0)$ に対して反比例のグラフと上図の領域が交点を持つことがわかる。

次に $t > 0$ の場合を考える。

$t > 0$ のときに反比例のグラフは第一象限と第三象限に存在する。

$0 < t < 2$ のとき, 図を見れば任意の $t$ に対して反比例のグラフと以下の領域が交点を持つことがわかる。

$$\begin{cases} b \gt -\dfrac{1}{4}a^2\\ -2 \lt a \lt 0\\ b \leqq a + 1\\ b \lt 0 \end{cases}$$

逆に $t \geqq 2$ のとき, 反比例のグラフと上図の領域は共有点を持たない。

以上より $ab$ の取りうる値の範囲は

$$ab < 2$$

である。