第3問
実数 a,b に対して
(a+cosα−cosβ)2+(b−sinα−sinβ)2(0≦α,β≦π)
の最小値を f(a,b) とおく。
(1) f(0,0) を求めよ。
(2) f(a,b)=0 となる (a,b) を ab 平面に図示したとき,その領域の面積を求めよ。
(3) f(a,b)≦4 となる (a,b) を ab 平面に図示したとき,その図形の周長を求めよ。
第3問は領域の問題でした。
まずは三角関数を丁寧に計算する解法を紹介します。
第3問 (1)
(cosα−cosβ)2+(sinα+sinβ)2=cos2α−2cosαcosβ+cos2β+sin2α+2sinαsinβ+sin2β=2−2(cosαcosβ−sinαsinβ)=2−2cos(α−β)
である。0≦α,β≦π であることから −π≦α−β≦π である。よって −1≦cos(α−β)≦1 が従う。
こうして 2−2cos(α−β)≧2−2=0 である。したがって f(0,0)=0 である。
次の解法は最大最小を求めるときのテクニックの1つです。今回の場合は f(0,0) が必ず 0 以上であることがわかりますから,後は実際に 0 を取るような α,β を与えると良いというわけです。
第3問 (1) 別解
f(0,0) は (cosα−cosβ)2+(sinα+sinβ)2 の最小値である。まず (cosα−cosβ)2+(sinα+sinβ)2≧0 である。
今,α=0,β=0 とすると,cosα−cosβ=1−1=0,sinα+sinβ=0+0=0 であるため,(cosα−cosβ)2+(sinα+sinβ)2 は 0 を取る。
こうして f(0,0)=0 となる。
与えられた式は (a,b) と (−cosα+cosβ,sinα+sinβ) の距離を表していることを踏まえると見通しが良くなります。
この視点を持つと,(1) は (−cosα+cosβ,sinα+sinβ) が (0,0) を取りうることを調べる問題だとわかります。
次の問題も距離を意識するとわかりやすいです。
第3問 (2)
(a+cosα−cosβ)2+(b−sinα−sinβ)2 は xy 平面上で2点 (a,b) と (−cosα+cosβ,sinα+sinβ) の距離の2乗である。
よって f(a,b)=0 となる (a,b) 領域は,α,β を任意に動かしたとき,(−cosα+cosβ,sinα+sinβ) の動く領域である。
−π≦α≦π,−π≦β≦π より (−cosα,sinα),(cosβ,sinβ) はそれぞれ半径 1 の円の上半分を動く。
中心が,原点を中心をする半径 1 の円の上半分となる半径 1 の円の上半分を動かして得られる軌跡,すなわち,(x−cosβ)2+(y−sinβ)2=1 の上半分について β を動かして得られる軌跡として次の図を得る。
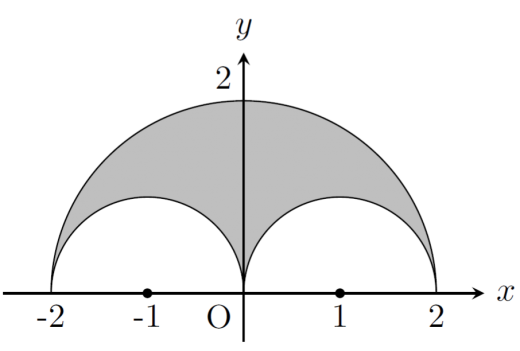
こうして求める面積は 4π⋅21−π⋅21⋅2=π
やはり (3) も距離のイメージで解くべきでしょう。要は (2) で得られた領域を「拡張」することになります。
第3問(3)
(−cosα+cosβ,sinα+sinβ) との距離が2以下になる (a,b) を考えればよいため,(2) で求めた図形を中心をする半径2の円の動く領域がを求めればよい。
b≧0 のとき
a2+b2=4 の円周上を中心とすることで,原点を中心とする半径 4 の円盤の上半分が求める領域だとわかる。
b≦0 のとき
(2) で求めた領域のうち b=0 上にある部分は (−2,0),(0,0),(2,0) の3点である。この3点を中心とする半径2の円を考えればよく,求める領域は b≦0 かつ以下
(a−2)2+b2≦4a2+b2≦4(a+2)2+b2≦4
のいずれかを満たす部分である。
3つの円の交点を求める。(a−2)2+b2=4 と a2+b2=4 の交点は (1,±3),(a+2)2+b2=4 と a2+b2=4 の交点は (−1,±3),(a−2)2+b2=4 と (a+2)2+b2=4 の交点は (0,0) となる。こうして求める領域は b≦0 かつ
⎩⎨⎧(a+2)2+b2≦4a2+b2≦4(a−2)2+b2≦4(−2≦a≦−1)(−1≦a≦1)(1≦a≦2)
である。
図示すると以下のようになる。
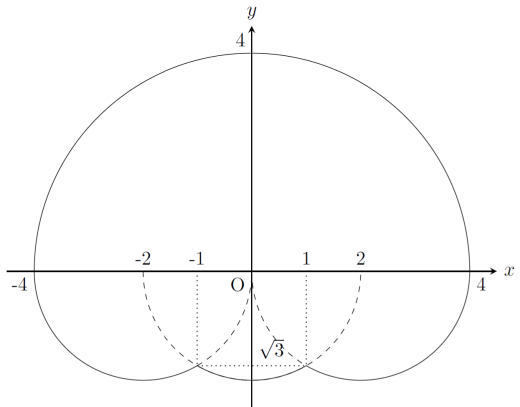
こうして外周は
4⋅π+2⋅(32π+31π+32π)=322π
となる。







