第2問
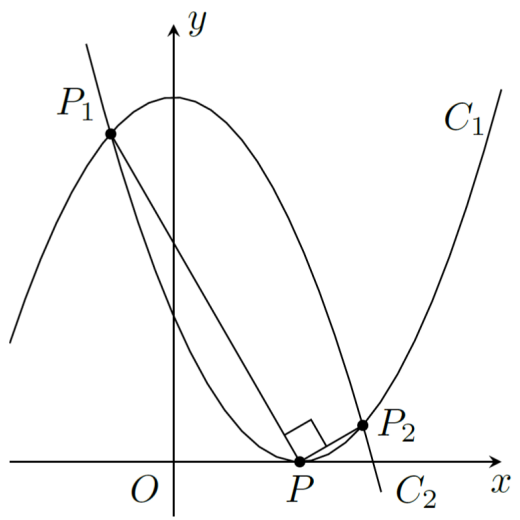
a , b a,b a , b x y xy x y C 1 : y = ( x − a ) 2 C_1: y=(x-a)^2 C 1 : y = ( x − a ) 2 C 2 : y = b − x 2 C_2: y = b-x^2 C 2 : y = b − x 2 P P P ( a , 0 ) (a,0) ( a , 0 )
以下の問いに答えよ。
(1) C 1 C_1 C 1 C 2 C_2 C 2 a , b a,b a , b
(2) 以下 a , b a,b a , b P 1 , P 2 P_1,P_2 P 1 , P 2 C 1 C_1 C 1 C 2 C_2 C 2 P 1 P_1 P 1 x x x b b b ∠ P 1 P P 2 = 9 0 ∘ \angle P_1 P P_2 = 90^{\circ} ∠ P 1 P P 2 = 9 0 ∘ a a a b b b
(3) 今,∠ P 1 P P 2 = 9 0 ∘ \angle P_1 P P_2 = 90^{\circ} ∠ P 1 P P 2 = 9 0 ∘ P , P 1 , P 2 P,P_1,P_2 P , P 1 , P 2 C C C C C C y y y b b b
(4) 円 C C C Q Q Q △ O P 2 Q \triangle OP_2Q △ O P 2 Q b b b
第2問は座標平面上の幾何の総合問題です。手が出にくいかもしれませんが,様々の方法で解くことができます。
(1) は判別式を計算する問題です。
第2問 (1)
b − x 2 = ( x − a ) 2 = x 2 − 2 a x + a 2 b-x^2 = (x-a)^2 = x^2 -2ax +a^2 b − x 2 = ( x − a ) 2 = x 2 − 2 a x + a 2 D = 2 b − a 2 D = 2b - a^2 D = 2 b − a 2 2 b − a 2 > 0 2b-a^2 >0 2 b − a 2 > 0
次の問題は交点を計算した上で,9 0 ∘ 90^{\circ} 9 0 ∘ 9 0 ∘ 90^{\circ} 9 0 ∘
ベクトルの内積が0
直線の傾きの積が-1
三平方の定理の逆
三角関数の計算
などが思いつきますね。今回は内積を用いるのが良いでしょう。方程式を立てて,a a a b b b a a a b b b
第2問 (2)
x 2 − 2 a x + a 2 = b − x 2 x^2 -2ax + a^2 =b-x^2 x 2 − 2 a x + a 2 = b − x 2 x = a ± 2 b − a 2 2 x = \dfrac{a\pm \sqrt{2b-a^2}}{2} x = 2 a ± 2 b − a 2 C 1 C_1 C 1 C 2 C_2 C 2 ( a ± 2 b − a 2 2 , b ∓ a 2 b − a 2 2 ) \left(\dfrac{a\pm \sqrt{2b-a^2}}{2},\dfrac{b\mp a\sqrt{2b-a^2}}{2}\right) ( 2 a ± 2 b − a 2 , 2 b ∓ a 2 b − a 2 )
条件よりP 1 ( a − 2 b − a 2 2 , b + a 2 b − a 2 2 ) P_1 \left(\dfrac{a- \sqrt{2b-a^2}}{2},\dfrac{b+ a\sqrt{2b-a^2}}{2}\right) P 1 ( 2 a − 2 b − a 2 , 2 b + a 2 b − a 2 ) P 2 ( a + 2 b − a 2 2 , b − a 2 b − a 2 2 ) P_2 \left(\dfrac{a+ \sqrt{2b-a^2}}{2},\dfrac{b- a\sqrt{2b-a^2}}{2}\right) P 2 ( 2 a + 2 b − a 2 , 2 b − a 2 b − a 2 )
P P 1 undefined = ( − a − 2 b − a 2 2 , b + a 2 b − a 2 2 ) P P 2 undefined = ( − a + 2 b − a 2 2 , b − a 2 b − a 2 2 )
\overrightarrow{PP_1} = \left(\dfrac{-a-\sqrt{2b-a^2}}{2}, \dfrac{b+ a\sqrt{2b-a^2}}{2}\right)\\
\overrightarrow{PP_2} = \left(\dfrac{-a+\sqrt{2b-a^2}}{2}, \dfrac{b- a\sqrt{2b-a^2}}{2}\right)
P P 1 = ( 2 − a − 2 b − a 2 , 2 b + a 2 b − a 2 ) P P 2 = ( 2 − a + 2 b − a 2 , 2 b − a 2 b − a 2 ) ∠ P 1 P P 2 = 9 0 ∘ \angle P_1 P P_2 = 90^{\circ} ∠ P 1 P P 2 = 9 0 ∘ P P 1 undefined ⋅ P P 2 undefined = 0 \overrightarrow{PP_1} \cdot \overrightarrow{PP_2} = 0 P P 1 ⋅ P P 2 = 0 P P 1 undefined ⋅ P P 2 undefined = − a − 2 b − a 2 2 ⋅ − a + 2 b − a 2 2 + b + a 2 b − a 2 2 ⋅ b − a 2 b − a 2 2 = a 2 − ( 2 b − a 2 ) 4 + b 2 − a 2 ( 2 b − a 2 ) 4 = 1 4 ( a 4 − 2 ( b − 1 ) a 2 + b 2 − 2 b ) = 1 4 ( a 2 − b ) ( a 2 − b + 2 ) \begin{aligned}
\overrightarrow{PP_1} \cdot \overrightarrow{PP_2} &= \dfrac{-a-\sqrt{2b-a^2}}{2} \cdot \dfrac{-a+\sqrt{2b-a^2}}{2} +\dfrac{b+ a\sqrt{2b-a^2}}{2} \cdot \dfrac{b- a\sqrt{2b-a^2}}{2}\\
&= \dfrac{a^2 - (2b-a^2)}{4} + \dfrac{b^2 - a^2(2b-a^2)}{4}\\
&= \dfrac{1}{4} (a^4 - 2(b-1)a^2 +b^2-2b)\\
&= \dfrac{1}{4} (a^2 - b)(a^2 -b+2)
\end{aligned} P P 1 ⋅ P P 2 = 2 − a − 2 b − a 2 ⋅ 2 − a + 2 b − a 2 + 2 b + a 2 b − a 2 ⋅ 2 b − a 2 b − a 2 = 4 a 2 − ( 2 b − a 2 ) + 4 b 2 − a 2 ( 2 b − a 2 ) = 4 1 ( a 4 − 2 ( b − 1 ) a 2 + b 2 − 2 b ) = 4 1 ( a 2 − b ) ( a 2 − b + 2 )
以上より
( a 2 − b ) ( a 2 − b + 2 ) = 0
(a^2 - b)(a^2 -b+2)=0
( a 2 − b ) ( a 2 − b + 2 ) = 0 a 2 = b a^2 = b a 2 = b P P 1 undefined = ( 0 , 0 ) \overrightarrow{PP_1} = (0,0) P P 1 = ( 0 , 0 ) ∠ P 1 P P 2 = 9 0 ∘ \angle P_1 P P_2 = 90^{\circ} ∠ P 1 P P 2 = 9 0 ∘ a 2 = b − 2 a^2 = b-2 a 2 = b − 2 a a a b − 2 b-2 b − 2 b > 2 b>2 b > 2
次の問題は三角形の外接円と y y y △ P P 1 P 2 \triangle PP_1P_2 △ P P 1 P 2 x = 0 x=0 x = 0
第2問 (3)
C C C △ P P 1 P 2 \triangle PP_1 P_2 △ P P 1 P 2 ∠ P 1 P P 2 = 9 0 ∘ \angle P_1 P P_2 = 90^{\circ} ∠ P 1 P P 2 = 9 0 ∘ P 1 P 2 P_1 P_2 P 1 P 2 C C C C C C P 1 P_1 P 1 P 2 P_2 P 2 C C C ( b − 2 2 , b 2 ) \left( \dfrac{\sqrt{b-2}}{2} , \dfrac{b}{2} \right) ( 2 b − 2 , 2 b )
( x − b − 2 2 ) 2 + ( y − b 2 ) 2 = b 2 + b − 2 4
\left(x-\dfrac{\sqrt{b-2}}{2} \right)^2 + \left( y- \dfrac{b}{2} \right)^2 = \dfrac{b^2+b-2}{4}
( x − 2 b − 2 ) 2 + ( y − 2 b ) 2 = 4 b 2 + b − 2 C C C x = 0 x=0 x = 0 b − 2 4 + ( y − b 2 ) 2 = b 2 + b − 2 4 ( y − b 2 ) 2 = b 2 4 y = b 2 ± b 2 = 0 , b \begin{aligned}
\dfrac{b-2}{4} + \left( y- \dfrac{b}{2} \right)^2 &= \dfrac{b^2+b-2}{4}\\
\left( y- \dfrac{b}{2} \right)^2 &= \dfrac{b^2}{4}\\
y &= \dfrac{b}{2} \pm \dfrac{b}{2} \\
&= 0,b
\end{aligned} 4 b − 2 + ( y − 2 b ) 2 ( y − 2 b ) 2 y = 4 b 2 + b − 2 = 4 b 2 = 2 b ± 2 b = 0 , b ( 0 , 0 ) , ( 0 , b ) (0,0),(0,b) ( 0 , 0 ) , ( 0 , b )
実は方程式を解かなくても点の座標を求めることができます。どのようなアイデアかというと,直線と円の交点が高々2点であることを踏まえて,条件を満たす2点を挙げる方法です。前回の入試数学コンテストの第3問でも,2直線の交点が高々1つであることを用いた論証をしました。このように「高々 n n n n n n
第2問 (3) 別解
C C C Q Q Q Q ( b − 2 2 , b 2 ) Q \left( \dfrac{\sqrt{b-2}}{2} , \dfrac{b}{2} \right) Q ( 2 b − 2 , 2 b )
O R undefined = O Q undefined + P Q undefined \overrightarrow{OR} = \overrightarrow{OQ} + \overrightarrow{PQ} OR = OQ + PQ R R R R R R P P P Q Q Q R R R C C C R R R O R undefined = O Q undefined + P Q undefined = 2 O Q undefined − O P undefined = 2 ( b − 2 2 b 2 ) − ( b − 2 0 ) = ( b 0 ) \begin{aligned}
\overrightarrow{OR} &= \overrightarrow{OQ} + \overrightarrow{PQ}\\
&= 2\overrightarrow{OQ} - \overrightarrow{OP}\\
&=2\begin{pmatrix} \dfrac{\sqrt{b-2}}{2} \\ \dfrac{b}{2} \end{pmatrix} - \begin{pmatrix} \sqrt{b-2}\\0 \end{pmatrix}\\
&= \begin{pmatrix} b\\0 \end{pmatrix}
\end{aligned} OR = OQ + PQ = 2 OQ − OP = 2 ⎝ ⎛ 2 b − 2 2 b ⎠ ⎞ − ( b − 2 0 ) = ( b 0 ) R R R y y y
Q Q Q x x x M M M M M M ( b − 2 2 , 0 ) \left( \dfrac{\sqrt{b-2}}{2} , 0 \right) ( 2 b − 2 , 0 ) O P OP OP O Q = O M 2 + M Q 2 = P M 2 + M Q 2 = P Q \begin{aligned}
OQ &= \sqrt{OM^2 + MQ^2}\\
&= \sqrt{PM^2 + MQ^2}\\
&= PQ
\end{aligned} OQ = O M 2 + M Q 2 = P M 2 + M Q 2 = PQ
したがって O O O C C C
以上より ( 0 , 0 ) , ( 0 , b ) (0,0),(0,b) ( 0 , 0 ) , ( 0 , b ) C C C y y y ( 0 , 0 ) , ( 0 , b ) (0,0),(0,b) ( 0 , 0 ) , ( 0 , b )
最後の問題は条件が単純ですが,何をするべきか思いつきにくいでしょう。大きく3つの方針が思いつきます。
三辺の大きさが等しいこと
1つの角が 6 0 ∘ 60^{\circ} 6 0 ∘
三角の大きさが等しい
どれをやるにしてもやることが多いように思うかもしれません。しかし (3) から O Q = Q P 2 OQ=QP_2 OQ = Q P 2
第2問 (4) 1番の方法
(3) より C C C Q Q Q O , P 2 O,P_2 O , P 2 O Q = Q P 2 OQ = QP_2 OQ = Q P 2 O Q = O P 2 OQ = OP_2 OQ = O P 2 b b b a = b − 2 a=\sqrt{b-2} a = b − 2 P 2 P_2 P 2 ( b − 2 + b + 2 2 , b − b 2 − 4 2 ) \left(\dfrac{\sqrt{b-2}+ \sqrt{b+2}}{2},\dfrac{b- \sqrt{b^2-4}}{2}\right) ( 2 b − 2 + b + 2 , 2 b − b 2 − 4 ) O Q = O P 2 O Q 2 = O P 2 2 1 4 ( b 2 + b − 2 ) = ( b − 2 + b + 2 2 ) 2 + ( b − b 2 − 4 2 ) 2 = 1 2 { b 2 + b − 2 − ( b − 1 ) b 2 − 4 } b 2 + b − 2 = 2 ( b − 1 ) b 2 − 4 \begin{aligned}
OQ&=OP_2\\
OQ^2 &= OP_2^2\\
\dfrac{1}{4} (b^2+b-2) &= \left(\dfrac{\sqrt{b-2}+ \sqrt{b+2}}{2}\right)^2 + \left( \dfrac{b- \sqrt{b^2-4}}{2} \right)^2\\
&= \dfrac{1}{2} \{ b^2+b-2 -(b-1) \sqrt{b^2-4} \}\\
b^2+b-2 &= 2(b-1) \sqrt{b^2-4}
\end{aligned} OQ O Q 2 4 1 ( b 2 + b − 2 ) b 2 + b − 2 = O P 2 = O P 2 2 = ( 2 b − 2 + b + 2 ) 2 + ( 2 b − b 2 − 4 ) 2 = 2 1 { b 2 + b − 2 − ( b − 1 ) b 2 − 4 } = 2 ( b − 1 ) b 2 − 4 b > 2 b>2 b > 2 b − 1 ≠ 0 b-1 \neq 0 b − 1 = 0 b − 1 b-1 b − 1 b + 2 = 2 b 2 − 4
b+2 = 2 \sqrt{b^2-4}
b + 2 = 2 b 2 − 4 b 2 + 4 b + 4 = 4 b 2 − 16 3 b 2 + 4 b − 20 = 0 b = − 2 , 10 3
b^2 + 4b+4 = 4b^2 -16\\
3b^2 +4b -20 = 0\\
b = -2 ,\dfrac{10}{3}
b 2 + 4 b + 4 = 4 b 2 − 16 3 b 2 + 4 b − 20 = 0 b = − 2 , 3 10 b > 2 b>2 b > 2 b = 10 3 b = \dfrac{10}{3} b = 3 10
第2問 (4) 2番の方法
条件から ∠ Q O P 2 = 6 0 ∘ \angle QOP_2 = 60^{\circ} ∠ QO P 2 = 6 0 ∘ O Q OQ OQ x x x ϕ \phi ϕ O P 2 OP_2 O P 2 x x x θ \theta θ Q ( b − 2 2 , b 2 ) Q \left( \dfrac{\sqrt{b-2}}{2} , \dfrac{b}{2} \right) Q ( 2 b − 2 , 2 b ) P 2 ( b − 2 + b + 2 2 , b − b 2 − 4 2 ) P_2 \left(\dfrac{\sqrt{b-2}+\sqrt{b+2}}{2} , \dfrac{b-\sqrt{b^2-4}}{2}\right) P 2 ( 2 b − 2 + b + 2 , 2 b − b 2 − 4 ) tan ϕ = b b − 2 tan θ = b − b 2 − 4 b − 2 + b + 2
\tan \phi = \dfrac{b}{\sqrt{b-2}}\\
\tan \theta = \dfrac{b-\sqrt{b^2-4}}{\sqrt{b-2}+\sqrt{b+2}}
tan ϕ = b − 2 b tan θ = b − 2 + b + 2 b − b 2 − 4 tan ( ϕ − θ ) = b b − 2 − b − b 2 − 4 b − 2 + b + 2 1 + b b − 2 b − b 2 − 4 b − 2 + b + 2 = ( b + 2 + b − 2 ) b − ( b − b 2 − 4 ) b − 2 b − 2 + b 2 − 4 + b 2 − b b 2 − 4 = 2 ( b − 1 ) b + 2 ( b − 1 ) ( b + 2 − b 2 − 4 ) = 2 b + 2 − b − 2 \begin{aligned}
&\tan (\phi - \theta)\\
&= \dfrac{\dfrac{b}{\sqrt{b-2}}-\dfrac{b-\sqrt{b^2-4}}{\sqrt{b-2}+\sqrt{b+2}}}{1+\dfrac{b}{\sqrt{b-2}} \dfrac{b-\sqrt{b^2-4}}{\sqrt{b-2}+\sqrt{b+2}}}\\
&= \dfrac{(\sqrt{b+2}+\sqrt{b-2})b - (b-\sqrt{b^2-4})\sqrt{b-2}}{b-2+\sqrt{b^2-4}+b^2-b\sqrt{b^2-4}}\\
&= \dfrac{2(b-1)\sqrt{b+2}}{(b-1)(b+2-\sqrt{b^2-4})}\\
&= \dfrac{2}{\sqrt{b+2}-\sqrt{b-2}}
\end{aligned} tan ( ϕ − θ ) = 1 + b − 2 b b − 2 + b + 2 b − b 2 − 4 b − 2 b − b − 2 + b + 2 b − b 2 − 4 = b − 2 + b 2 − 4 + b 2 − b b 2 − 4 ( b + 2 + b − 2 ) b − ( b − b 2 − 4 ) b − 2 = ( b − 1 ) ( b + 2 − b 2 − 4 ) 2 ( b − 1 ) b + 2 = b + 2 − b − 2 2 ϕ − θ = ± 6 0 ∘ \phi - \theta = \pm 60^{\circ} ϕ − θ = ± 6 0 ∘ ϕ \phi ϕ θ \theta θ ± \pm ± 2 b + 2 − b − 2 = ± 3
\dfrac{2}{\sqrt{b+2}-\sqrt{b-2}} = \pm \sqrt{3}
b + 2 − b − 2 2 = ± 3 4 3 = 2 b − 2 b 2 − 4 3 b − 2 = 3 b 2 − 4
\dfrac{4}{3} = 2b-2\sqrt{b^2-4}\\
3b-2 = 3\sqrt{b^2-4}
3 4 = 2 b − 2 b 2 − 4 3 b − 2 = 3 b 2 − 4 9 b 2 − 12 b + 4 = 9 b 2 − 36 12 b = 40 b = 10 3
9b^2 - 12b +4 = 9b^2 -36\\
12b = 40\\
b=\dfrac{10}{3}
9 b 2 − 12 b + 4 = 9 b 2 − 36 12 b = 40 b = 3 10 b = 10 3 b = \dfrac{10}{3} b = 3 10
意外と答えはすっきりした数になります。
配点 25点
(1) [4点]
2 b − a 2 > 0
2b-a^2 >0
2 b − a 2 > 0
(2) [5点]
b > 2
b>2
b > 2
(3) [各3点]
( 0 , 0 ) , ( 0 , b )
(0,0),(0,b)
( 0 , 0 ) , ( 0 , b )
(4) [10点]
b = 10 3
b = \dfrac{10}{3}
b = 3 10