浮力の原理「アルキメデスの原理」と例題
この記事では,流体圧の基本性質である浮力について説明します。いくつかの面白い例題を通して,中学校で学んだ内容よりやや定量的に,厳密に理解することが目標です。
浮力の定義
浮力の定義
流体(空気や水)の中にある物体の表面が,流体から受ける圧力の合力のことを浮力と言います。一般に浮力の方向は鉛直上向きとは限らないので注意してください。一般に流体圧の合力を調べるのは,大学レベルの高度な数学が必要になります。しかし浮力の場合は,次に紹介するアルキメデスの原理を適用することで簡単に調べることができます。
この記事に関連するQ&A
アルキメデスの原理
アルキメデスの原理
物体にはたらく浮力に関する基本的な原理である,アルキメデスの原理を紹介します。
流体中に入れた物体にはたらく浮力の大きさは,物体が排除した流体に働く重力の大きさに等しく,向きは重力の反対方向である。
以下の流体中の点線部分を考える。点線部分の流体は,点線部分外の流体と全く同じ流体であることに注意する。流体の密度を ,点線部分の流体の体積を とすると,点線部分の受ける重力は であることがわかる。今,点線部分の流体は流体の中で静止しているので,重力につり合う力がはたらいている。つまり,点線部分の流体が点線部外の流体から受ける圧力の合力(浮力)は,この場合上向き であるとわかる。

この議論は点線部分がどのような形でも成り立つ。また,浮力は点線部分外の流体から点線部分の流体への流体圧の合力なので,点線部分に他の物体を入れても,はたらく浮力の大きさは, である。向きについても結論を得る。
流体の浮力については,基本的にこのアルキメデスの原理を用いて考えていくことになります。
重力と慣性力がある場合の問題
重力と慣性力がある場合の問題
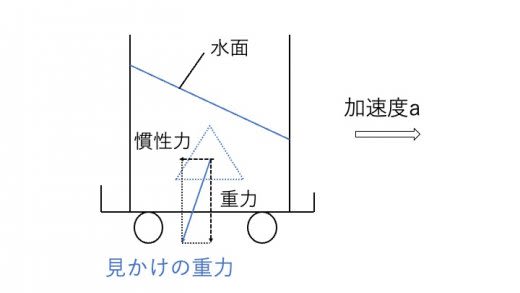
荷台に密度 の流体の入った水槽が乗っている。この荷台を右向き一定の加速度 を与えて運動させた。このとき体積 の点線部分の受ける浮力の大きさを求めよ。

荷台と一緒に運動する座標系で見ると,点線部分にはたらく見かけの重力は,.
流体部分は静止しているので,力のつりあいより,浮力は見かけの重力と反対の方向にはたらき,大きさは である。
慣性力については,こちらの記事を参考にしてください。
慣性力があるために,見かけの重力の向きが,鉛直上向きではない場合を考えました。水面の向きは,見かけの重力の向きと直行することに注意してください。この場合もアルキメデスの原理を導いた時と同様の議論により,浮力の大きさと向きを求めることができます。
水面の上昇についての問題
水面の上昇についての問題
密度一様の氷がコップの中の水に浮いている。この氷が全て溶けた時,水面は上昇するか,下降するか。

氷の沈んでいる部分の体積を ,水の密度を ,氷全体の質量を とする。力のつりあいは,
これを整理して, を得る。氷が溶けて水になった時, は変化しないので,これは質量 の氷が溶けて水になった時,体積が になることを示している。
以上より,水面の高さは変化しない。
感覚的にわかりづらいこのような系も,アルキメデスの原理により詳しく調べることができます。
浮力による単振動の問題
浮力による単振動の問題
図のように,密度 の水が入ったプールに,長さ ,質量 ,断面積 の棒状の浮きを浮かべた。
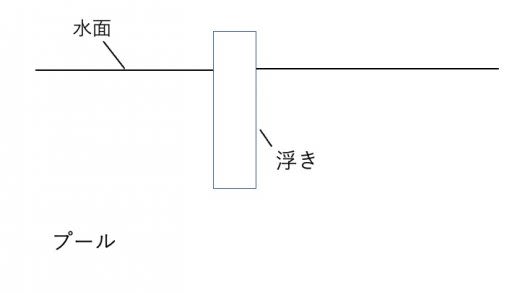 (1)浮きは横揺れすることなく,鉛直方向にのみ運動するとする。浮きを静止状態からわずかに下に引っ張って離したところ,浮きは周期運動を始めた。この周期運動の周期を求めよ。
(1)浮きは横揺れすることなく,鉛直方向にのみ運動するとする。浮きを静止状態からわずかに下に引っ張って離したところ,浮きは周期運動を始めた。この周期運動の周期を求めよ。
(2)下図のように,浮きが鉛直方向から横に微小な角度だけ傾いた。この後,浮きはそのまま回転するか,元の状態に戻るか。

(1)鉛直方向下向きに 軸をとり,水面の高さを原点,浮きの最下点の位置の座標を とおく。このとき,アルキメデスの原理より,浮きにはたらく浮力は 軸負の向きで,大きさは . よって運動方程式を立てると,
これは を振動中心とする,周期 の単振動。

(2)浮力は浮きの沈んでいる部分の重心にはたらくことに注意する。浮きの重心周りのトルク(モーメント)を考えると,浮力は角度の微小なずれを増長するようにはたらく。よって浮きはそのまま回転する。
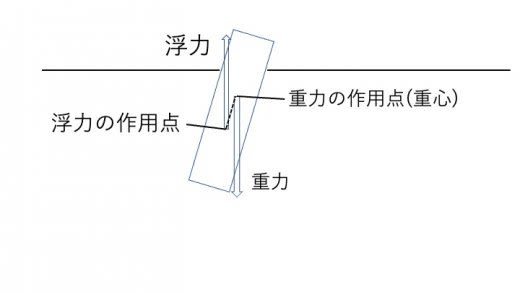
この場合,この系は不安定つりあいであるということができます。
例題中の単振動については,こちらを参照してください。
またトルク(モーメント)や,剛体の回転についてはこちらを参照してください。
浮力を考えるときは,必ずアルキメデスの原理から出発するようにしましょう。











