摩擦力の定義|動摩擦力・静止摩擦力・摩擦係数の解説
この記事では,まず摩擦力の根源的な原因を説明し,その後に摩擦力に関する各用語の定義を解説します。基本的な概念なので,曖昧さを残さず理解することが重要です。
抗力の定義
抗力の定義
摩擦力の定義を行う前に,まずその元となる概念である,抗力について説明します。
あなたは今,椅子に座っていたり,床に立っていたりして,その状態で静止していると思います。力のつり合いにより,椅子や床から,あなたは何らかの力を受けていることになります。このように,物体(皆さんの身体)が別の物体(椅子や床)に接触しているときに受ける反発力を抗力と言います。
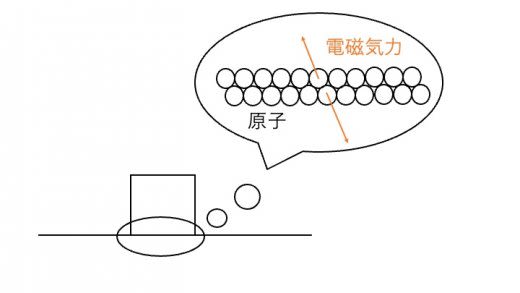
では,なぜこのような力が生じるのでしょうか?実は抗力とは,物体同士の接触面の分子の電磁気的な力によって生じた力であることが知られています。
この記事に関連するQ&A
摩擦力の定義
摩擦力の定義
以下の図は,人が床に立って静止している状態を表しています。このとき人は加速度を持っていないので,人に働く力はつりあいの状態にあると考えられます。ではつりあいの式を水平方向と鉛直方向に分けて書いてみます。以下では鉛直上向き,水平右向きをそれぞれ正方向とおきます。
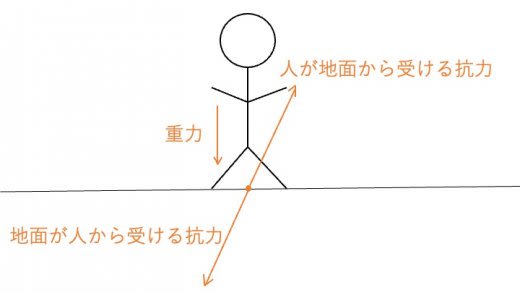
水平方向:
鉛直方向:
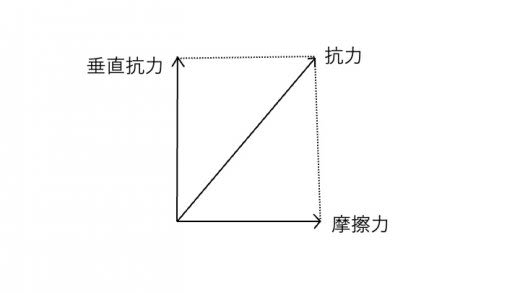
ここでは抗力を水平方向と鉛直方向に分解し,水平方向を ,鉛直方向を と表しています。抗力を分解した, のことを摩擦力, のことを垂直抗力と言います。
上のつりあいの式を解くことで, となります。よって上の例では摩擦力の大きさが0,垂直抗力は鉛直上向きで,大きさは となることがわかります。
静止摩擦力と動摩擦力
静止摩擦力と動摩擦力
注意しなければならないのは,物体同士が接触しているとき,抗力(摩擦力,垂直抗力)は必ず存在するということです。そして,抗力の大きさや向きは必ず運動方程式によってのみ指定されます。 私たちが最初に得られる情報は,いかなる場合でも抗力が「ある」ということだけであって,抗力の「大きさ,向き」はわからないのです。したがって,摩擦力を求める公式は運動方程式ということになります。
物体が他の物体が接触しながら運動している場合も抗力(摩擦力,垂直抗力)が存在します。このように,物体が動いているときに生じる摩擦力を,特に動摩擦力と言います。また,物体が静止しているときの摩擦力を静止摩擦力と言います。
静止摩擦係数と最大静止摩擦力
静止摩擦係数と最大静止摩擦力
以下の図の例を考えてみましょう。斜面に物体が静止しています。このとき鉛直方向に力がつりあっているので,重力とつりあう抗力があることがわかります。また,抗力はこの方向以外にないこともわかります。

ここで,斜面の角度 を徐々に大きくしていくとどうなるでしょうか? ある角度 を超えると,物体は徐々に下に滑り始めるはずです。図より,ここで抗力が斜面鉛直方向となす角も,図形的に となります。静止摩擦力を ,垂直抗力を と書くと,物体が滑り始めない条件を以下のように表すことができます。
ここで無次元の係数 を静止摩擦係数と言います。また, より, となり,静止摩擦力は を超えないことがわかります。よって のことを最大摩擦力(最大静止摩擦力)と言います。
動摩擦係数
動摩擦係数
これまでは静止摩擦力を考えましたが,以下では動摩擦力を考えます。引き続き同じ例を見てみましょう。斜面を傾けて となるとき,物体は下に動き始めます。このときの動摩擦力を ,垂直抗力を と書くと,同様に
と表すことができます。 は接触している物体の性質(金属なのか,木材なのかなど)と,滑り方によって決まると考えられる,無次元の定数です。この を動摩擦係数と言います。動摩擦係数を用いて動摩擦力は と表されることがわかります。タイヤなどの転がる物体が受ける動摩擦力の動摩擦係数を,転がり摩擦係数と呼ぶこともあります。
実は は物体の滑り方によらず,いつもほぼ一定とみなせることが実験的にわかっています。 理由は今でもよくわかっていません。
また,一般に であることが知られています。
上と同じ固定された斜面に同じ物体を置いた。 の時,物体は滑り始めた。斜面と物体の間の動摩擦係数を動摩擦係数を とする。
(1)物体に働く動摩擦力の大きさと向きを求めよ。
(2)物体の加速度の大きさを求めよ。
まず運動方程式を立てる。
下図より,斜面水平方向と斜面鉛直方向の運動方程式はそれぞれ
水平方向:
鉛直方向:
となる。
(1)鉛直方向の運動方程式より を得る。よって,求める動摩擦力は,
(2)水平方向の運動方程式にに(1)で求めた を代入して, を得る。
例題の中でも注意して欲しいのが,摩擦力の向き,大きさの求め方は,いつも運動方程式であるということです。物体が進む向きと反対方向に抵抗を受けるというイメージでだけでは,動摩擦力の向きがわかりづらい系もあります。
摩擦は高校物理でよく扱われる題材ではありますが,現代でも解明されていないことが多いです。










