張力の性質と種々の例題
高校物理の問題では頻繁に現れる張力ですが,張力とは何なのかを詳しく教わることはあまりないのではないでしょうか。 ここでは,張力の持つ性質と,いくつかの例題について説明します。
張力の性質
張力の性質
張力とは何か
張力とは,基本的には,「糸(及びそれに準ずる装置)が物体を引っ張る力」を意味します。この記事では,一般の張力の話をするときは,簡単のため,糸による張力を考えることにします。
一般には,糸及び物体を構成する分子間で作用する分子間力が,その源になっています。したがって,ふつう張力の働く方向は,私たちが直感的にイメージする方向と同方向に作用しています。
張力の作用点ですが,ここは少し注意が必要です。というのも,糸と繋がっている物体,どちらがどちらに及ぼしていると考えるのかで,作用点の位置も変化してくるからです。 (作用・反作用の記事もご覧ください:作用反作用の法則〜ニュートンの第3法則〜)
張力とは「糸が物体を引っ張る力」でしたから,その作用点は,糸と物体が接する点Pのうち物体側の方となります。つまり下図のようになります。
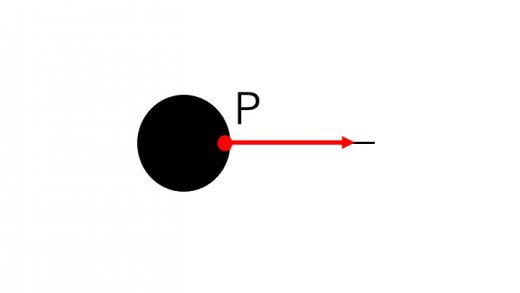
逆に,張力の反作用,つまり「物体が糸に及ぼす力」を考える際には,その作用点は点Pのうち糸側の方になります。つまり下図のようになります。

この,「どちらがどちらに及ぼす力なのか」という考え方は,Newtonの運動方程式を考える際に重要となるので,しっかり身につけるようにしてください。
また,張力は非保存力であり,張力による位置エネルギーを考えることはできません。張力の仕事は経路に依って異なるからです。 (詳しくは:位置エネルギーの定義と例(重力・弾性力・クーロン力))
張力の大きさ
Newtonの運動方程式を解く際,張力の大きさを考えることが重要になってきます。 高校物理でよく使われる「軽い」糸の張力については,次の公式が成り立ちます。
ちなみに,高校物理では,「軽い」という表現は 糸の質量は無視して良いということを表しています。
張力は糸のどの場所でも等しい。
これを証明してみましょう。
簡単のため,糸が直線状にピンと伸びている場合を考えます。糸は十分軽いとみなして良いとします。糸に沿った軸を考えます。点 で糸が 軸正方向に引っ張る張力を とおきます。微小領域 にある糸について,力のつり合いが成り立つので
とすると,微分の定義により
この証明で用いたように,「微小区間に分けて考える」という考え方は,物理の勉強で非常に重要かつ頻出です。
計算の結果,張力の値が0以下の値になってしまったとき,その糸は物理的には「弛む」状態になります。また,糸がピンと張っているならば,その糸は物体を引っ張る方向に張力を生み出しています。ですから,張力を考慮して運動方程式を立てる時には,張力は「私たちが直感的に考える方向に働いている」と考えて組み込んで良いことになります。
張力による種々の運動
張力による種々の運動
では,よく取り扱われる運動の例について幾つか紹介してみます。
糸と同方向に動く運動
物体が糸と同じ方向に運動するときの運動を例題で見てみましょう。
図のように,質量 の物体A,Bが,滑車を通じて糸で結ばれている場合を考える。物体Bを に静かに離したときの,物体A,Bの 秒後の変位を求めよ。

滑車を介する本問のように,糸が途中で方向を変える場合にも,張力は糸の至る所で同じです。物体A,Bの変位をそれぞれ ,張力を として, 運動方程式を立てます。
ここで,未知数は の3つですから,もう一つ式が必要になります。
そこで,束縛条件に注目しましょう。2物体は張った糸で繋がれていますから,2物体は同じ分だけ移動します。すなわち
です。
(1)+(2)より,
(3)より
あとは,初期条件より , として良いので,等加速度運動の公式 (詳しくは:等加速度運動・等加速度直線運動の公式) より, 秒後の物体A,Bの変位は, となります。
(3)を導いたところがこの問題のミソですね。
張力と直交する方向に運動する場合
続いて,物体が張力と直交する運動を考えてみましょう。 こちらは先程の例に比べてやや考察が必要となります。
まずは円運動を考えてみましょう。高校物理の頻出分野の一つですね。「直交」が大きな意味を持ってきます。
図のように,壁に打ち付けられた釘に取り付けられた,長さ の糸に,質量 のおもりがぶら下がっている。糸は軽く,糸と釘の摩擦は無視できるものとする。最下点から速度 でおもりを動かすとき,次の問いに答えよ。

(1)図のように,おもりの位置を角 で表す。この位置でのおもりの速さを求めよ。
(2)おもりが円軌道を一周するための の条件を求めよ。
(1)糸のおもりに対する張力を ,位置 でのおもりの速度を とすると,半径方向の運動方程式は以下のように書き下せます。
しかし,半径に垂直な方向の運動方程式は,高校物理の範囲では書き下すことができません。Coriolis力などを考慮しなければならないからです。
ここで,運動の方向と張力が直交していることに着目すると,張力による仕事が0になることを導くことができます。これは別の記事で解説します。
これにより,最下点と位置 で力学的エネルギー保存則が成立します。 なので,これを解いて, を得ます。
(2)少し物理的な考察をしてみましょう。おもりが一周するのはどのようなときでしょうか。
まず,頂点で速さが0より大きくなければならないということは分かりますね。力学的エネルギー保存則を考えれば,上に行くほどおもりの速さは減少します。頂点に行くまでに速さが0になってしまえば,その後は重力の影響を受けて,おもりは元来た軌道を引き返してしまいます。つまり頂点に到達するには,おもりはその途中で一度も0にならないことが求められます。逆に,頂点で速さが正の値であれば,その途中で速さは常に正であったことが,力学的エネルギー保存則より保証されます。
では,頂点で速さが正の値になっていれば,必ずおもりは一周するのでしょうか。張力が0,つまり糸が弛んでいる場合はどうでしょう。このとき,おもりは円ではない軌道を描いてしまいますね。つまり,頂点で張力が正の値となることも求められるということになります。
では,解答例に戻りましょう。
頂点でのおもりの速さを とします。 頂点における(2.1),(2.3)式は, を代入して, ここで,おもりが円を一周するためには,先程の物理的考察により,
が必要。として良いから,(2.5),(2.6)式より,
また,(2.4),(2.5),(2.7)式より,
よって,(2.8),(2.9)式をともに満たすの条件として,
を得ます。これが求める答えとなります。
円運動を続けるためには張力が正の値とならなければならない,ということがポイントです。
次に単振り子の運動を考えます。Galileiが示したことで知られる,「振り子の等時性」を示すことができます。
図のような,長さ の糸,質量 の物体からなる単振り子を考える。この単振り子の周期を求めよ。ただし,振幅は十分小さいとして良く,糸に働く摩擦は無視して良い。

解答例に移る前に,三角関数の近似についてよく用いる公式を紹介します。
角 が微小であるとき,以下が成り立つ。
ここで, は,「近似的に等しい」ことを表す記号である。
(2)については, が0に近いと考えることで,ああそうだな,となると思います。
(1)については,数3で習う以下の極限の公式から分かります。ここでは詳しい証明は省略します。
この公式は,「 が十分小さい時には, と が等しい」ことを表していると解釈できます。
では解答例に移りましょう。
振り子の位置を で表し,物体の水平方向の変位をで表します。 は微小だとして良いので,垂直方向の変位は0として考えて構いません。従って垂直方向の加速度は0になります。運動方程式より
まず(3.2)式より
また,三角形の辺の長さの関係より
(3.1),(3.3)式より,
これは「単振動の方程式」と呼ばれる方程式であり,高校物理でも頻出の式となります。詳しくは単振動のまとめを見ていただくことにして,ここでは結果だけを述べることにします。
(3.4)式の解は,
ただし, であり, として与えられます。この単振り子の周期は,周期の公式 (詳しくは:正弦波の意味,特徴と基本公式) より,
となります。
この結果から分かるように, 単振り子の周期は振り子の重さや初期条件によらず, 振り子の長さのみによって決まります。
【発展】解析力学における張力
【発展】解析力学における張力
大学では,解析力学という分野を勉強します。簡単に言うと,解析力学とは,古典力学の持つ数学的性質を抽出することで,古典力学を含む物理学の様々な領野をより統一的に,深く学ぼうとする学問です。
解析力学で使われる方程式は,Euler-Lagrange方程式と呼ばれるものです。 この式の中で重要な働きをする「ラグランジアン」と呼ばれる物理量は,力学的エネルギーと位置エネルギーから決まります。張力は非保存力でしたから,位置エネルギーを生み出すことはなく,解析力学においては,「一般化力」としてラグランジアンとは別の扱いをうけます。
高校物理と張力は,まさに「切っても切れない存在」です。つまりチョー大事。張力だけに。
張力を使った問題はこの他にも色々な設定があり,張力の奥深さが感じられます。様々な問題に触れてみてくださいね。











