ポテンシャル障壁とトンネル効果

ポテンシャル障壁とは，以下のような形をしたポテンシャルのことです。

数式で表すと

$$\begin{aligned} V(x)= \begin{cases} 0 & (x \leq 0, \, a \leq x) \\ V_0 (>0) & (0 < x < a) \tag{☆} \end{cases} \end{aligned}$$

のようになります。

時間に依存しないシュレディンガー方程式を解く

いま，粒子のエネルギー $E$ がポテンシャル障壁の高さ $V_0$ より小さい場合のことを考えます。考えているポテンシャルは全領域において時間に依存しない実数となっているので，シュレディンガー方程式の解を $\psi (x,t) = T(t) \phi(x)$ と変数分離して考えることができます(詳しくは定常状態におけるシュレディンガー方程式の一般解)。

考えるべきは固有関数 $\phi$ のかたちであり，$\phi$ は以下のように時間に依存しないシュレディンガー方程式を満たします。

$$\begin{aligned} -\dfrac{\hbar^2}{2m} \dfrac{\partial^2}{\partial x^2} \phi = \begin{cases} E \phi & (x \leq 0, \, a \leq x) \qquad (2-1)\\ (E - V_0) \phi & (0 < x < a) \qquad (2-2) \end{cases} \end{aligned}$$

1次元箱型ポテンシャルの解，有限の井戸型ポテンシャルでの議論により，固有関数 $\phi$ は

$$\begin{aligned} \phi(x) = \begin{cases} \phi_L(x) = A_+ e^{ikx} + A_- e^{-ikx}& (x \leq 0) \\ \phi_C(x) = B_+ e^{k'x} + B-_ e^{-kx} & (0 < x < a) \\ \phi_R(x) = C_+ e^{ikx} + C_- e^{-ikx} & (a \leq x) \tag{☆☆} \end{cases} \end{aligned}$$

のように書くことができます。ただし，$k$，$k'$ は正の実数であり

$$k = \sqrt{\dfrac{2mE}{\hbar^2}} \, , \, k' = \sqrt{\dfrac{2m(V_0 - E)}{\hbar^2}}$$

を満たしています。

係数どうしの関係を求める

波動関数の連続性

いま，$x = - \infty$ から $x$ 軸正方向に粒子を入射することを考えます。このとき，$a < x$ を $x$ 軸負方向に進む粒子は存在しないと考えられるので，$C_- = 0$ と考えることができます。

$x = 0, a$ での波動関数の連続性(詳しくは有限の井戸型ポテンシャル)から係数どうしの関係を求めていきます。以下では $\dfrac{\partial f}{\partial x} = f'(x)$ と略記します。

$x = 0$ での波動関数の連続性より

$$\begin{aligned} \begin{cases} \phi_L(0) = \phi_C(0) \qquad (1)\\ \phi_L'(0) = \phi_C'(0) \qquad (2)\\ \end{cases} \end{aligned}$$

(☆☆)より，代入して

$$\begin{aligned} \begin{cases} A_+ + A_- = B_+ + B_- \qquad (1')\\ ik(A_+ - A_-) = k' (B_+ - B_-) \qquad (2')\\ \end{cases} \end{aligned}$$

が得られます。

また，$x = a$ での波動関数の連続性より

$$\begin{aligned} \begin{cases} \phi_C(a) = \phi_R(a) \qquad (3)\\ \phi_C'(a) = \phi_R'(a) \qquad (4)\\ \end{cases} \end{aligned}$$

(☆☆)より，代入して

$$\begin{aligned} \begin{cases} B_+ e^{k'a} + B_- e^{-k'a} = C_+ e^{ika} \qquad (3')\\ k'(B_+ e^{k'a} - B_- e^{-k'a}) = ik C_+ e^{ika}\qquad (4')\\ \end{cases} \end{aligned}$$

が得られます。

$A_+, A_-$ を $B_+, B_-$ で表す

(2’)より

$$A_+ - A_- = \dfrac{k'}{ik} (B_+ - B_-) \tag{5}$$

と変形できます。(1)，(5)より

$$\begin{aligned} A_+ &= \dfrac{1}{2} \left\{\left(1 + \dfrac{k'}{ik} \right ) B_+ + \left(1 - \dfrac{k'}{ik} \right ) B_- \right \} \\ & = \dfrac{ik(B_+ + B_-) + k'(B_+ - B_-)}{2ik} \end{aligned} \tag{6}$$

$$\begin{aligned} A_- &= \dfrac{1}{2} \left\{\left(1 - \dfrac{k'}{ik} \right ) B_+ + \left(1 + \dfrac{k'}{ik} \right ) B_- \right \} \\ & = \dfrac{ik(B_+ + B_-) - k'(B_+ - B_-)}{2ik} \end{aligned} \tag{7}$$

と表すことができました。

$B_+, B_-$ を $C_+$ で表す

(4’)より

$$B_+ e^{k'a} - B_- e^{-k'a} = \dfrac{ik}{k'} C_+ e^{ika} \tag{8}$$

のように変形できます。(3’)，(8)より

$$\begin{aligned} B_+ e^{k'a} &= \dfrac{1}{2} C_+ e^{ika} \left(1 + \dfrac{ik}{k'} \right ) \\ & = \dfrac{k' + ik}{2k'} C_+ e^{ika} \end{aligned}$$

$$\begin{aligned} B_- e^{-k'a} &= = \dfrac{k' - ik}{2k'} C_+ e^{ika} \end{aligned}$$

$$\begin{aligned} \therefore \begin{cases} B_+ &= \dfrac{k' + ik}{2k'} C_+ e^{(ik - k')a} & (9)\\ B_- &= \dfrac{k' - ik}{2k'} C_+ e^{(ik + k')a} & (10) \\ \end{cases} \end{aligned}$$

が得られます。

$A_+, A_-$ を $C_+$ で表す

(9)，(10)より

$$\begin{aligned} B_+ + B_- &= \dfrac{1}{2k'} \{(k' + ik) e^{-k'a} + (k' - ik) e^{k'a} \} C_+ e^{ika} \\ &= \dfrac{1}{k'} (k' \cosh{(k'a)} - ik \sinh{(k'a)}) C_+ e^{ika} \end{aligned}$$

$$\begin{aligned} B_+ - B_- &= \dfrac{1}{2k'} \{(k' + ik) e^{-k'a} - (k' - ik) e^{k'a} \} C_+ e^{ika} \\ &= \dfrac{1}{k'} (- k' \sinh{(k'a)} + ik \cosh{(k'a)}) C_+ e^{ika} \end{aligned}$$

が得られます。

これらを(6)，(7)に代入して

$$\begin{aligned} A_+ &= \dfrac{1}{2ikk'} [ik(k' \cosh{(k'a)} - ik \sinh{(k'a)}) \\ & \quad + k' (- k' \sinh{(k'a)} + ik \cosh{(k'a)})] C_+ e^{ika} \\ &= \left(\cosh{(k'a)} + i \dfrac{k'^2 - k^2}{2kk'} \sinh{(k'a)} \right ) C_+ e^{ika} \qquad (11) \end{aligned}$$

$$\begin{aligned} A_- &= \dfrac{1}{2ikk'} [ik(k' \cosh{(k'a)} - ik \sinh{(k'a)}) \\ & \quad - k' (- k' \sinh{(k'a)} + ik \cosh{(k'a)})] C_+ e^{ika} \\ &= -i \dfrac{k'^2 + k^2}{2ikk'} \sinh{(k'a)} C_+ e^{ika} \qquad (12) \end{aligned}$$

が得られます。

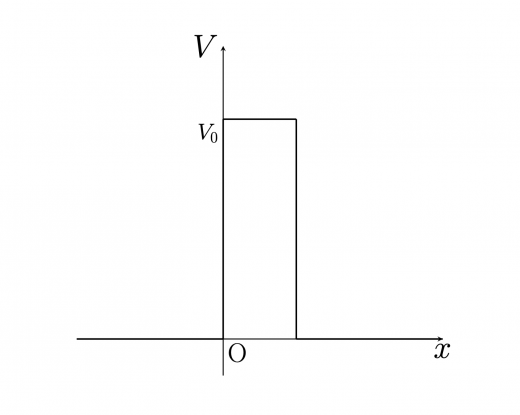
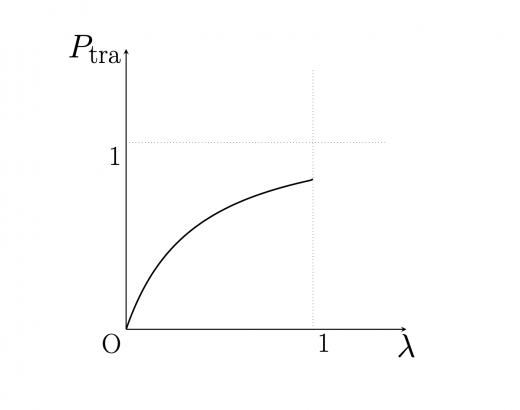引き続き，$E < V_0$ で考えていきます。 ポテンシャル障壁に入射した粒子はどのような挙動を示すか考えていきます。古典力学では，自身のエネルギー $E$ がポテンシャルの高さ $V_0$ を下回る場合には，そのポテンシャルを乗り越えることはできませんでしたが，量子力学ではどうなるでしょうか。

透過率を求める

$x < 0, a < x$ での粒子の流れを計算していきます。

ボルンの確率解釈(確率規則)，階段型ポテンシャルの解での議論より，$x < 0$ での粒子の流れ $J_{x < 0}$ は

$$J_{x < 0} = \dfrac{\hbar}{m} \text{Im} \left(\phi_L^* \phi_L' \right)$$

と求めることができるのでした。ここで

$$\phi_L^* = A_+^* e^{-ika} + A_-^* e^{ika} \, , \, \phi_L' = ik(A_+ e^{ika} - A_- e^{ika})$$

$$\begin{aligned} \therefore \phi_L^* \phi_L' &= (A_+^* e^{-ika} + A_-^* e^{ika}) \cdot ik(A_+ e^{ika} - A_- e^{ika}) \\ &= ik (|A_+|^2 - A_+^* A_- e^{-2ika} + A_-^* A_+ e^{2ika} - |A_-|^2 ) \\ &= ik(|A_+|^2 - |A_-|^2 + 2i \text{Im} (A_+ A_-^* e^{2ika})) \\ &= ik(|A_+|^2 - |A_-|^2) - 2k \text{Im} (A_+ A_-^* e^{2ika}) \end{aligned}$$

ゆえに

$$J_{x < 0} = \dfrac{\hbar k}{m} (|A_+|^2 - |A_-|^2)$$

$x = - \infty$ から入射する粒子の流れ $J_\text{inc} (- \infty \to 0)$ は

$$J_{\text{inc}} (- \infty \to 0) = \dfrac{\hbar k}{m} |A_+|^2$$

と表すことができます。

同様にして，$a < x$ の領域に透過していく粒子の流れ $J_{\text{tra}} \, (a \to \infty)$ は

$$\begin{aligned} J_{\text{tra}} \, (a \to \infty) &= \dfrac{\hbar k}{m} \text{Im} \left(\phi_R^* \phi_R' \right) \\ &= \dfrac{\hbar k}{m} |C_+|^2 \end{aligned}$$

と求めることができます。

したがって，$x = - \infty$ から入射した粒子が $a < x$ の領域に透過していく確率 $P_{\text{tra}}$ は，(11)より

$$\begin{aligned} P_{\text{tra}} &= \dfrac{|J_{\text{tra}} \, (a \to \infty)|}{|J_{\text{inc}} (- \infty \to 0)|} \\ &= \dfrac{|C_+|^2}{|A_+|^2} \\ &= \left|\dfrac{C_+}{A_+} \right | \\ &= \left|\left(\cosh{(k'a)} + i \dfrac{k'^2 - k^2}{2kk'} \sinh{(k'a)} \right )^{-1}e^{-ika} \right|^2 \\ &= |\cosh{(k'a)} + i \dfrac{k'^2 - k^2}{2kk'} \sinh{(k'a)} |^{-2} \\ &= [(\cosh{(k'a)})^2 + (\dfrac{k'^2 - k^2}{2kk'}) (\sinh{(k'a)})^2 ]^{-1} \\ &= [1 + \left(1 + \dfrac{k'^4 - 2k'^2 k^2 + k^4}{4k'^2 k^2 } \right ) (\sinh{(k'a)})^2]^{-1} \\ &= [1 + \left(\dfrac{k'^2 + k^2}{2k k'} \right )^2 (\sinh{(k'a)}) ^2]^{-1} \tag{13} \end{aligned}$$

のように求めることができます。ただし，上の式変形において，第4行から第5行，第5行から第6行，第6行から第7行へは，それぞれ

$$|e^{i \theta}| = 1 \quad (\theta \in \mathbb{R})$$

$$|a + ib|^2 = a^2 + b^2 \quad (a, b \in \mathbb{R})$$

$$(\cosh{x})^2 - (\sinh{x})^2 =1 (x \in \mathbb{R})$$

が成り立つことを用いています。これらについては，詳しくは

• 複素数の絶対値の定義といろいろな性質

• オイラーの公式と複素指数関数

• 双曲線関数(sinh,cosh,tanh)の意味・性質・楽しい話題まとめ

をご覧ください。

トンネル効果

(13)式より，

$$0 < P_{\text{tra}} < 1$$

が成り立っていることがわかります。これより，量子力学においては，粒子は自身のエネルギーより大きいポテンシャルをある一定の確率で透過することがわかります。このことをトンネル効果と呼びます。

$P_{\text{tra}}$ を $E$ と $V_0$ で表してみましょう。シュレディンガー方程式を解く過程で

$$k = \sqrt{\dfrac{2mE}{\hbar^2}} \, , \, k' = \sqrt{\dfrac{2m(V_0 - E)}{\hbar^2}}$$

という関係が得られていました。

ここから

$$\begin{aligned} (2kk')^2 &= \left(2 \sqrt{\dfrac{2mE}{\hbar^2}} \sqrt{\dfrac{2m(V_0 - E)}{\hbar^2}} \right)^2 \\ &= 16 \dfrac{m^2}{\hbar^4} E (V_0 - E) \end{aligned}$$

$$\begin{aligned} (k'^2 + k^2)^2 &= \left(\dfrac{2mE}{\hbar^2} + \dfrac{2m(V_0 - E)}{\hbar^2} \right )^2 \\ &= \left(\dfrac{2mV_0 }{\hbar^2} \right )^2 \\ &= 4 \dfrac{m^2}{\hbar^4} V_0^2 \end{aligned}$$

$$\begin{aligned} \therefore \left(\dfrac{k'^2 + k^2}{2kk'} \right)^2 &= \dfrac{4 \dfrac{m^2}{\hbar^4} V_0^2}{16 \dfrac{m^2}{\hbar^4} E (V_0 - E)} \\ &= \dfrac{V_0^2}{4E(V_0-E)} \\ &= [4 \dfrac{E}{V_0} \left(1 - \dfrac{E}{V_0} \right )]^{-1} \end{aligned}$$

が得られます。(13)より

$$\begin{aligned} P_{\text{tra}}&= [1 + \left(\dfrac{k'^2 + k^2}{2k k'} \right )^2 (\sinh{(k'a)}) ^2]^{-1} \\ &= \left[1 + \dfrac{\left(\sinh{\left(a \sqrt{\dfrac{2m V_0}{\hbar}\left(1 - \dfrac{E}{V_0} \right )} \right )} \right )^2 }{4 \dfrac{E}{V_0} \left(1 - \dfrac{E}{V_0} \right )} \right ]^{-1} \end{aligned}$$

$0 < E < V_0$ より，$\dfrac{E}{V_0} = \lambda$ とおくと，$0 < \lambda < 1$ であり，$P_{\text{tra}}$ は

$$P_{\text{tra}} = \left[1 + \dfrac{\left(\sinh{\left(a \sqrt{\dfrac{2m V_0}{\hbar}\left(1 - \lambda \right )} \right )} \right )^2 }{4 \lambda \left(1 - \lambda \right )} \right ]^{-1}$$

と表すことができます。

これをグラフに表すと下図のようになります。

【補足】確率の保存

$x = 0$ で粒子が反射される確率 $P_{\text{ref}}$ を求めてみましょう。これまでの議論と同様に考えて，$P_{\text{ref}}$ は

$$\begin{aligned} P_{\text{ref}} &= \left|\dfrac{A_-}{A_+} \right|^2 \\ &= \left|\dfrac{-i \dfrac{k'^2 + k^2}{2ikk'} \sinh{(k'a)}}{\cosh{(k'a)} + i \dfrac{k'^2 - k^2}{2kk'} \sinh{(k'a)}} \right |^2 \\ &= \dfrac{\left(\dfrac{k'^2 + k^2}{2ikk'} \right )^2 (\sinh{(k'a)})^2 }{1 + \left(\dfrac{k'^2 + k^2}{2k k'} \right )^2 (\sinh{(k'a)}) ^2} \end{aligned}$$

のように求められます。これと(13)より

$$P_{\text{tra}} + P_{\text{ref}} = 1$$

が成り立っていることがわかります。

2つの極限について透過率を考察してみます。

極限1：$k'a >> 1$ のとき

これは $E << V_0$ (つまり $E/V_0 << 1$) または $a >> 1$ を表しています。

$x << 1$ (つまり $x$ が十分大きい) のとき

$$\sinh{x} = \dfrac{e^{x} - {e^{-x}}}{2} \simeq \dfrac{e^x}{2} >> 1$$

を用いて，$P_{\text{tra}}$ を評価すると

$$\begin{aligned} P_{\text{tra}} &= \left[1 + \left(\dfrac{k'^2 + k^2}{2k k'} \right )^2 (\sinh{(k'a)}) ^2 \right ]^{-1} \\ & \simeq \left(\dfrac{\dfrac{1}{4} \exp{\left(2a \sqrt{\dfrac{2m(V_0 - E)}{\hbar^2}} \right )}}{4 \dfrac{E(V_0 - E)}{V_0^2 }} \right )^{-1} \\ & \simeq 16 \dfrac{E(V_0 - E)}{V_0^2} \exp{\left(-2a \sqrt{\dfrac{2m(V_0 - E)}{\hbar^2}} \right )} \\ & = 16 \dfrac{E}{V_0} \left(1 - \dfrac{E}{V_0} \right) \exp{\left(-2a \sqrt{\dfrac{2mV_0}{\hbar^2} } \sqrt{1 - \dfrac{E}{V_0 }}\right )} \end{aligned}$$

と表せます。指数関数を用いて表すことができた点に注意してください。

極限2：$E \simeq V_0$ のとき

$E < V_0$ かつ $E \simeq V_0$ のときを考えます。このとき，微小な正の実数 $\varepsilon \, (0 < \varepsilon << 1)$ を用いて

$$E = V_0 (1 - \varepsilon)$$

と表すことができます。このとき $E/V_0 = (1 - \varepsilon)$ なので

$$P_{\text{tra}} = \left[1 + \dfrac{\left(\sinh{\left(a \sqrt{\dfrac{2mV_0}{\hbar^2} \varepsilon} \right )} \right)^2 }{4 \varepsilon (1 - \varepsilon)} \right ]^{-1}$$

と表すことができます。

ここで，$x << 1$ のとき

$$\begin{aligned} \sinh{x} &= \dfrac{e^x - e^{-x}}{2} \\ & \simeq \dfrac{1 + x - (1 - x)}{2} \\ & \simeq x \end{aligned}$$

と評価できるので，$P_{\text{tra}}$ は

$$\begin{aligned} P_{\text{tra}} &= \left[1 + \dfrac{a^2 \dfrac{2mV_0}{\hbar^2} \varepsilon}{4 \varepsilon (1 - \varepsilon)} \right ]^{-1} \\ &= \left[1 + \dfrac{a^2 mV_0}{2 \hbar^2} \dfrac{1}{1 - \varepsilon} \right ]^{-1} \\ &= \dfrac{(1- \varepsilon)}{(1- \varepsilon) + \dfrac{a^2 mV_0}{2 \hbar^2}} \\ &= 1 - \dfrac{\dfrac{a^2 mV_0}{2 \hbar^2}}{1- \varepsilon + \dfrac{a^2 mV_0}{2 \hbar^2}} \\ &= 1 - \dfrac{a^2 mV_0}{2 \hbar^2} \dfrac{1}{1 + \dfrac{a^2 mV_0}{2 \hbar^2}} \dfrac{1}{1 - \left(1 + \dfrac{a^2 mV_0}{2 \hbar^2} \right )^{-1} \varepsilon} \end{aligned}$$

ここで，$\varepsilon$ の 1 次以上の項を $O(\varepsilon)$ と表すことにすると，$\dfrac{1}{1-x}$ のマクローリン展開(詳しくはマクローリン展開)を利用して

$$\begin{aligned} P_{\text{tra}} & \simeq 1 - \left(\dfrac{a^2 mV_0}{2 \hbar^2 + a^2 mV_0} - O(\varepsilon) \right ) \\ &= \dfrac{2 \hbar^2}{2 \hbar^2 + a^2 mV_0} + O(\varepsilon) \\ &= \left(1 + \dfrac{mV_0}{2 \hbar^2} \right )^{-1} + O(\varepsilon) \end{aligned}$$

と評価できます。

$\varepsilon$ が非常に小さく，$\varepsilon$ の1次以上の項を無視できるとすると

$$P_{\text{tra}} \simeq \left(1 + \dfrac{mV_0}{2 \hbar^2} \right )^{-1}$$

このときも，$0 < P_{\text{tra}} < 1$ であり，一定の確率でトンネル効果が起こることがわかります。