有限の井戸型ポテンシャル

以降，簡単のため1次元で考えていきます。

有限の深さの井戸型ポテンシャルとは(以降この記事では「井戸型ポテンシャル」と呼びます)，以下のように図示できるポテンシャルのことを指します。

式で表すと以下のようになります。

$$\begin{aligned} V(x)= \begin{cases} 0 & (-L \leq x \leq L) \\ V_0 & (x < - L, L < x) \tag{☆} \end{cases} \end{aligned}$$

ここで，$V_0$ は正の実数となっています。

今回考える井戸型ポテンシャルは時刻 $t$ に依存しないかたちになっています。変数分離法によって解を求めていきましょう。(この解き方については，詳しくは定常状態におけるシュレディンガー方程式の一般解をご覧ください。)

波動関数 $\psi$ が $\psi = \phi(x) T(t)$ と表せると考えると，シュレディンガー方程式は以下の二つの方程式に分けられます。

$T$ は(2)から簡単に求められ，

$$T(t) \propto \exp{\left(- \dfrac{i E t}{\hbar} \right)}$$

$$\therefore \psi = C \phi(x) \exp{\left(- \dfrac{i E t}{\hbar} \right)}$$

ここで，$C$ は定数です。

(1)の固有状態となるような関数 $\phi(x)$ を求めていきましょう。

以下では関数 $\phi(x)$ に対して，以下の条件が成り立っているとします。

• 十分遠方にて $\psi \to 0$，つまり $\phi(x) \to 0$ となる。 (＊1)

• 全領域での $|\phi(x)|^2$ の積分は有限の値を持つとする。 (＊2)

• 箱の内外いずれでも，自明な解は，それ以外の解を持たない限り考えないことにする。 (＊3)

条件(＊1)を満たすような解を，束縛状態の解などと呼びます。

(1)は時間に依存しないシュレディンガー方程式とも呼ばれます。ハミルトニアンの中身を具体的に書き出すと以下のようになります。

$$\left(- \dfrac{\hbar^2}{2m} \dfrac{\partial^2}{\partial x^2}+ V(x) \right) \phi = E \phi(x)$$

いま，ポテンシャルは(☆)のかたちを考えているので，シュレディンガー方程式は以下のように場合分けできます。

$$\begin{aligned} -\dfrac{\hbar^2}{2m} \dfrac{\partial^2}{\partial x^2} \phi = \begin{cases} (E -V_0) \phi & (-L \leq x \leq L) \qquad(2-1)\\ V_0 \phi & (x < - L, L < x) \qquad(2-2) \end{cases} \end{aligned}$$

箱の外側と内側とで場合分けして解いていきます。

箱の外側，すなわち $|x| > L$ のときの固有状態を求めていきます。

粒子のエネルギー $E$ とポテンシャル $V_0$　との大小で場合分けしていきます。

粒子のエネルギーが井戸のポテンシャルより大きいとき

まず，$E - V_0 > 0$，すなわち $E > V_0$ のときを考えます。このとき(2-2)は

$$\begin{aligned} \dfrac{\partial^2}{\partial x^2} \phi &= - \dfrac{2 m (E - V_0)}{\hbar^2} \phi \\ &= - K^2 \phi \qquad(3) \end{aligned}$$

ここで，$K$ は正の実数で，

$$K^2 = \dfrac{2 m (E - V_0)}{\hbar^2}$$

を満たします。

微分方程式(3)の解は

$$\phi = A_{+} \exp{(i K x)} + A_{-} \exp{(- i K x)}$$

と得られます。$A_{+}, A_{-}$ は初期条件などにより定まる定数です。

この $\phi$ に対し，

$$\begin{aligned} |\phi|^2 &= (A_{+}^* \exp{(- i K x)} + A_{-}^* \exp{( i K x)}) \\ & \quad \cdot (A_{+} \exp{(i K x)} + A_{-} \exp{(- i K x)}) \\ &= |A_{+}|^2 + |A_{-}|^2 + 2(A_{+}^* A_{-} + A_{-}^* A_{+}) \end{aligned}$$

この値は $x$ に依存していないことに注意してください。いま，自明な解は考えていないので，$A_{+}, A_{-}$ のうち少なくとも一方は $0$ ではありません。このとき，十分遠方でも $|\phi|^2$，すなわち $\phi$ は $0$ ではない有限の値を持つことになり，(＊1)に矛盾します。

これより，$A_{+}, A_{-}$ はどちらも $0$ でなければならず，自明な解となります。したがって，この場合の解は考えなくてよいことになります。

粒子のエネルギーが井戸のポテンシャルより小さいとき

では，$E < V_0$ のときを考えます。このとき(2-1)は

$$\begin{aligned} \dfrac{\partial^2}{\partial x^2} \phi &= \dfrac{2 m (V_0 - E)}{\hbar^2} \phi \\ &= k'^2 \phi \tag{4} \end{aligned}$$

ここで，$k'$ は正の定数で

$$k'^2 = \dfrac{2m(V_0 - E)}{\hbar^2} \quad \text{i.e.} \quad k = \dfrac{\sqrt{2m(V_0 - E)}}{\hbar}$$

となるような数です。

微分方程式(4)の一般解は

$$\phi = B_{+} \exp{(k' x)} + B_{-} \exp{( - k' x)}$$

と表せます。ここに，$B_{+}, B_{-}$ は初期条件などから定まる定数です。

この $\phi$ に対し，

$$\begin{aligned} |\phi|^2 &= (B_{+}^* \exp{(k' x)} + B_{-}^* \exp{( - k' x)}) \\ &\quad \cdot(B_{+} \exp{(k' x)} + B_{-} \exp{( - k' x)}) \\ &= |B_{+}|^2 \exp{(2 k' x)} + |B_{-}|^2 \exp{(- 2 k' x)} + 2(B_{+}^* B_{-} + B_{-}^* B_{+}) \end{aligned}$$

まず，井戸の左側，すなわち $x < - L$ のときを考えます。このとき，$|\phi|^2$ のこの領域での積分が有限の値となるためには，$x \to - \infty$ で $|\phi|^2$ の値が $0$ に収束する必要があります。そのためには

$$B_{-} = 0$$

である必要があります。したがって，$x < - L$ での解は

$$\phi = B_{+} \exp{(k' x)}$$

のかたちで書き表せます。

井戸の右側，つまり $L < x$ でも同様に考えることができます。この領域での$|\phi|^2$ のこの領域での積分が有限の値となるためには，$x \to \infty$ で $|\phi|^2$ の値が $0$ に収束する必要があります。そのためには

$$B_{-} = 0$$

である必要があります。したがって，$L < x$ での解は

$$\phi = B_{-} \exp{(- k' x)}$$

のかたちで書き表せます。

定数を新たに置き直して，箱の外側での解は

$$\begin{aligned} \phi(x)= \begin{cases} B \exp{(k' x)} & (-L < x) \\ D \exp{(- k' x)} & (L < x) \end{cases} \end{aligned}$$

のかたちで表すことができます。

続いて，箱の内側，すなわち $- L \leq x \leq L$ での解を考えていきます。

このとき時間に依存しないシュレディンガー方程式は

$$\dfrac{\partial^2}{\partial x^2} \phi = - \dfrac{2 m E}{\hbar^2} \phi \tag{5}$$

微分方程式(5)は，1次元の箱型ポテンシャルで考えた，箱の中での時間に依存しないシュレディンガー方程式と同じ形となっています。したがって，(5)は $E > 0$　の場合だけを考えればよく，その条件下で一般解は

$$\phi = C_1 \sin{kx} + C_2 \cos{kx}$$

と表すことができます。ここに，$k$ は正の定数で

$$k = \dfrac{\sqrt{2mE}}{\hbar}$$

となるような数です。また $C_1, C_2$ は初期条件などから定まる定数です。

全領域での波動関数のかたちをまとめておきましょう。

$$\begin{aligned} \phi(x)= \begin{cases} \phi_1 = B \exp{(k' x)} & (-L < x) \\ \phi_2 = C_1 \sin{kx} + C_2 \cos{kx} & (-L \leq x \leq L)\\ \phi_3 = D \exp{(- k' x)} & (L < x) \end{cases} \end{aligned}$$

1次元の箱型ポテンシャルのときと同様に，波動関数の連続性から，定数どうしの関係を決めていきます。

波動関数の連続性とは

波動関数の連続性とは，ポテンシャルの変わる境界で $\phi$ はなめらかにつながっていなければならないとするものです。境界条件や接続条件とも呼ばれます。

ポテンシャル $V$ が全領域で無限に発散せず有限の値を持つことより，ポテンシャルの変わる境界で，波動関数の値だけでなく，波動関数の微分係数の値が等しいことも条件として要請します。

井戸型ポテンシャルの場合

今回考える井戸型ポテンシャルでは $x = \pm L$ でポテンシャルが変わります。したがって，この値で境界条件を考えます。以下では簡単のため，$\dfrac{\partial f}{\partial x}(x) = f'(x)$ と略記します。

$x = -L$ での境界条件より

$$\begin{aligned} \left \{ \begin{aligned} & \phi_1(-L) = \phi_2(-L) \qquad (6)\\ & \phi_1'(-L) = \phi_2'(-L) \qquad (7) \end{aligned} \right. \end{aligned}$$

$$\therefore \begin{aligned} \left \{ \begin{aligned} & B \exp{(k' L)} = - C_1 \sin{kL} + C_2 \cos{kL} \qquad (6')\\ & k' B \exp{(k' L)} = C_1 \cos{kL} + C_2 \sin{kL} \qquad (7') \end{aligned} \right. \end{aligned}$$

また $x = L$ での境界条件より

$$\begin{aligned} \left \{ \begin{aligned} & \phi_2(L) = \phi_3(L) \qquad (8)\\ & \phi_2'(L) = \phi_3'(L) \qquad (9) \end{aligned} \right. \end{aligned}$$

$$\therefore \begin{aligned} \left \{ \begin{aligned} & C_1 \sin{kL} + C_2 \cos{kL} =D \exp{(k' L)} \qquad (8')\\ & k C_1 \cos{kL} - k C_2 \sin{kL} = - k' D \exp{(- k' L)} \qquad (9') \end{aligned} \right. \end{aligned}$$

(6’)~(9’)を変形していきます。$k$ と $k'$ との区別に注意してください。まず，(6’)と(7’)より $B$ を消去すると

$$k C_1 \cos{kL} + k C_2 \sin{kL} = k'(- C_1 \sin{kL} + C_2 \cos{kL})$$

$$\therefore C_1(k \cos{kL} + k' \sin{kL}) + C_2(k \sin{kL} - k' \cos{kL}) = 0 \quad (10)$$

また(8’)と(9’)から $D$ を消去すると

$$k C_1 \cos{kL} - k C_2 \sin{kL} = -k'(C_1 \sin{kL} + C_2 \cos{kL} ) = 0$$

$$\therefore C_1(k \cos{kL} + k' \sin{kL}) + C_2 (k' \cos{kL} - k \sin{kL}) = 0 \quad (11)$$

連立方程式(10)，(11)が $C_1 = C_2 = 0$ でないような解を持つような条件を考えます。(10)，(11)より

$$\dfrac{C_2}{C_1} = - \dfrac{k \cos{kL} + k' \sin{kL}}{k \sin{kL} - k' \cos{kL}} = - \dfrac{k \cos{kL} + k' \sin{kL}}{k' \cos{kL} - k \sin{kL}}$$

$$\begin{aligned} \therefore 0 &= (k \cos{kL} + k' \sin{kL})(k' \cos{kL} - k \sin{kL}) \\ & \quad - (k \cos{kL} + k' \sin{kL}) (k \sin{kL} - k' \cos{kL}) \end{aligned}$$

$$\therefore (k \cos{kL} + k' \sin{kL})(k' \cos{kL} - k \sin{kL}) = 0$$

すなわち

$$k \cos{kL} + k' \sin{kL} = 0 \tag{12-1}$$

$$\text{or}$$

$$k' \cos{kL} - k \sin{kL} = 0 \tag{12-2}$$

が条件として課されることになります。この $k$ と $k'$ とが満たす関係について，さらに場合分けしていきます。

(12-1)が成り立つとき

このとき，(10)または(11)より

$$C_2 (k \sin{kL} - k' \cos{kL}) = 0$$

ここで，$C_2$ が $0$ でないと仮定すると

$$k \sin{kL} - k' \cos{kL} = 0$$

が成り立ちます。いま，$k, k'$ はいずれも正の数なので，この式を

$$\dfrac{\sin{kL}}{\cos{kL}} = \tan{kL} = \dfrac{k}{k'} > 0$$

と変形することが許されます。しかし，これは(12-1)より

$$\tan{kL} = - \dfrac{k}{k'} < 0$$

が成り立つことに矛盾します。したがって，このとき $C_2 = 0$ でなければなりません。

さらに(6’)，(8’)より

$$\begin{aligned} \left \{ \begin{aligned} & B \exp{(-k' L)} = - C_1 \sin{kL} \\ & D \exp{(-k' L)} = C_1 \sin{kL} \end{aligned} \right. \end{aligned}$$

これより $D = -B$ であることがわかります。したがって，全領域での固有状態を，$B, C_1$ のみを用いて表すと

$$\begin{aligned} \phi(x)= \begin{cases} \phi_1 = B \exp{(k' x)} & (-L < x) \\ \phi_2 = C_1 \sin{kx} & (-L \leq x \leq L)\\ \phi_3 = -B \exp{(- k' x)} & (L < x) \tag{13} \end{cases} \end{aligned}$$

となります。

(注)$B$ と $C_1$ との間には

$$B \exp{(- k' L)} = - C_1 \sin{k L}$$

の関係があります。

これを代入して定数を一つにしてもよいです。今回は式が簡単になるので，定数は二つ用いています。

(12-2)が成り立つとき

このとき(10)または(11)より

$$C_1(k \cos{kL} + k' \sin{kL}) = 0$$

ここで，$C_2 \neq 0$ とすると，

$$k \cos{kL} + k' \sin{kL} = 0$$

(12-1)が成り立つときと同様に考えて，この式を

$$\tan{kL} = - \dfrac{k}{k'} < 0$$

と変形することが許されます。しかしこれは，(12-2)が成り立つことより，

$$\dfrac{\sin{kL}}{\cos{kL}} = \tan{kL} = \dfrac{k}{k'} > 0$$

が成り立つことに矛盾します。したがって，$C_1 = 0$ でなければなりません。

さらに(6’)，(8’)より，

$$\begin{aligned} \left \{ \begin{aligned} & B \exp{(-k' L)} = C_2 \cos{kL} \\ & D \exp{(-k' L)} = C_2 \cos{kL} \end{aligned} \right. \end{aligned}$$

$$\therefore D = B$$

したがって，全領域での固有状態を，$B, C_1$ のみを用いて表すと

$$\begin{aligned} \phi(x)= \begin{cases} \phi_1 = B \exp{(k' x)} & (-L < x) \\ \phi_2 = C_2 \cos{kx} & (-L \leq x \leq L)\\ \phi_3 = B \exp{(- k' x)} & (L < x) \tag{14} \end{cases} \end{aligned}$$

(注)$B$ と $C_1$ との間には

$$B \exp{(- k' L)} = C_2 \cos{k L}$$

の関係があります。

全体としての波動関数(13)，(14)は，それぞれ奇関数，偶関数になっています。これを証明しましょう。偶関数/奇関数の定義などについては，偶関数と奇関数の意味，性質などまとめをご覧ください。

ある $k$ に対して(13)をグラフで表してみると下図のようになります。

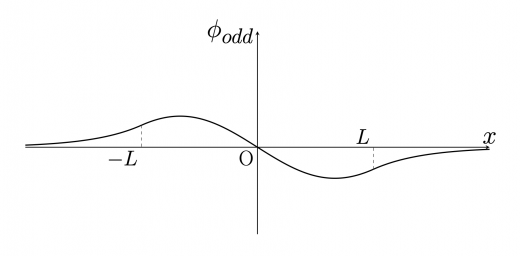
また，(14)をグラフで表してみると下図のようになります。

(13)，(14)がそれぞれ奇/偶関数であることが視覚的にもわかりますね。

上で示したように，全体としての波動関数 $\phi$ には，位置 $x$ についての偶関数と奇関数の両方が存在することがわかりました。 これを波動関数の 偶奇性(パリティ) と呼びます。例えば，波動関数が偶関数であるとき，その波動関数のパリティは偶である，などと使います。

波動関数のかたちを求める際に，$k$ と $k'$ についての条件式が導かれていました。それらからエネルギー固有値を求めてみましょう。

まず，$k$ と $k'$ の定義より

$$\begin{aligned} k^2 + k'^2 &= \dfrac{2m E}{\hbar^2} + \dfrac{2m (V_0 - E)}{\hbar^2} \\ &= \dfrac{2m V_0}{\hbar^2} \qquad (15) \end{aligned}$$

が成り立っています。

次に，$\phi$ が奇関数のときの条件式より

$$k \cos{kL} + k' \sin{kL} = 0$$

$$\therefore k' = - \dfrac{k}{\tan{kL}} \tag{16}$$

$\phi$ が偶関数のときの条件式より

$$k' \cos{kL} - k \sin{kL} = 0$$

$$k' = k \tan{kL} \tag{17}$$

(15)と(16)のグラフの交点が，$\phi$ が奇関数のときのエネルギー固有値であり，(15)と(17)のグラフの交点が，$\phi$ が偶関数のときのエネルギー固有値となります。

(15)，(16)，(17)を $k$-$k'$ 平面上でグラフに表してみましょう。

上図では，黒い実線が(17)，黒い破線が(16)，赤・橙・緑色の実線が(15)を表しています。赤<橙<緑の順でポテンシャル $V_0$ の値が大きくなっています。

つまり，色付きの実線と黒い実線との交点が，$\phi$ が偶関数のときの固有エネルギーとなり，色付きの実線と黒い破線との交点が，$\phi$ が奇関数のときの固有エネルギーとなります。

$k = \sqrt{2mE}/\hbar$ であることに注意すると，エネルギー固有値とそれに対応する固有状態の偶奇は，エネルギーが小さい方から順に，偶，奇，偶，…と交互に並ぶことがわかります。