シュレディンガー方程式の導出過程とその意味 -その1-

シュレディンガー方程式はオーストリアの物理学者であるシュレディンガー(墺, 1887-1961)によって示されました。シュレディンガーは, 1933年にノーベル物理学賞を受賞しており, 量子力学における「シュレディンガーの猫」という思考実験でも非常に有名です。

シュレディンガー方程式は「量子の世界を司る基本方程式」です。

量子の世界では物質は二重性(粒子性＋波動性)を強く持つため, 物質の粒子性だけに注目する運動方程式では電子の運動を厳密には記述するできません。

そのため, シュレディンガー方程式が必要になります。

シュレディンガー方程式：量子力学の基本方程式

シュレディンガー方程式は量子力学の基本方程式です。

すなわち,

• ニュートン力学における運動方程式 $m a = \boldsymbol{F}$

• 電磁気学におけるマクスウェル方程式（4つ）

のような関係にあたる, すべての記述の基本となる方程式です。

先に紹介したように, シュレディンガー方程式は3次元の偏微分方程式です。

$$i \hbar \dfrac{\partial}{\partial t} \psi(\boldsymbol{r},t) = \left( - \dfrac{\hbar^2}{2m} \nabla^2+ V(\boldsymbol{r}) \right) \psi(\boldsymbol{r},t)$$

ただ, この式を初めて見ると以下のような疑問が次々と湧いてくることでしょう。

1. 虚数単位 $i$ がなぜあるのか？
2. $\hbar$ とは何か？（読み方：エイチバー）
3. 関数 $\psi(r,t)$ （読み方：プサイ）とは何の関数か？
4. $\partial$ を使った偏微分は何を示すのか？

これらの疑問は, シュレディンガー方程式の導出の過程で解消されます。

以下で, 1つずつ理解していきましょう。

3次元シュレディンガー方程式は複雑なので, ポテンシャルエネルギー $V$ を含まない1次元のシュレディンガー方程式を考えてみましょう。

ポテンシャルエネルギーがないことを, 「自由粒子」や「束縛状態」と表現することもあります。

まず, シュレディンガー方程式に右辺に出現する $\psi(x,t)$ という関数について理解しましょう。

$\psi(x,t)$　とは波動関数であり, 位置 $x$, 時刻 $t$ の量子の状態を表現しています

つまり, 波動関数とは波の運動を記述した式です。

シュレディンガー方程式を解いて, $\psi(x,t)$ を求めることができれば, 量子状態を理解することができます。したがって, 量子状態は位置 $x$ と時刻 $t$ で決まると言えます。

量子力学における波動関数は, 現実世界と何が違うのでしょうか？

現実世界における観測事実，例えば「A君が午前10:00に東京タワーにいる」という状態は, 確定した状態です。

一方で, 波動関数が表すのはこのような確定した状態ではなく, その状態を取る「確率」です。「観測するまではどのような状態に確定するのかはわからないが, 波動関数によりその状態に確定する確率は知ることができる」という解釈するのです。

厳密には, $\psi(x,t)$ の絶対値の二乗 $|\psi(x,t)|^2$ が量子の存在確率を表現します。

シュレディンガー方程式を解けば, 存在確率 $|\psi(x,t)|^2$ を知ることができます。

力学で「運動方程式を解いたら位置 $x$ を時間 $t$ の関数で表すことができた」ということと同じような意味合いがあります。

このことは，一つの大見出しの中でさらっと説明できるようなものではありませんので，別記事で改めて紹介しようと思います。今の時点では，波動関数は確率の情報をもつ関数である，と認識しておいてください。

1次元シュレディンガー方程式の導出に移る前に, 導出方針を定めます。

シュレディンガー方程式の導出のスタート地点は電子の二重性, つまり電子が波であり粒子であるということです。

以下の3つの条件を満たすことを要請します（= 出発点としての前提にします）。

1. 波動方程式と波動関数

波動方程式（波の運動方程式）

$$\dfrac{\partial^2{y(x,t)}}{\partial^2{x} } = \dfrac{1}{c^2}\dfrac{\partial^2{y(x,t)}}{\partial^2{t}}$$

$y(x, t)$ は波動方程式を満たす波動関数です。電子は波動関数に従って運動するものと考えます。シュレディンガー方程式は波動方程式の特殊な場合で, $\psi(x,t)$ はシュレディンガー方程式を満たす波動関数です。

2. ドブロイ波長とエネルギーと振動数の関係式

• ドブロイ波長(ドブロイ方程式) →ドブロイ波長(物質波) $$\lambda = \dfrac{h}{p}$$

ドブロイ波長はド・ブロイが見つけた粒子である電子の波動性を表現した式です。この式一つで電子の二重性を示しています。

• エネルギーと振動数の関係 →エネルギーと振動数の関係(光電効果)

$$E = h \nu = \dfrac{h}{\lambda}$$

この式は光電効果から導かれた関係式で, 光の粒子性や光がとびとびのエネルギーを持つことを表現しています。

3. エネルギー保存則（ポテンシャルエネルギーは省略） $$E = \dfrac{1}{2}mv^2 = \dfrac{p^2}{2m} (\because p =mv)$$

これは電子や光が運動量をもった粒子であることを表しています。

「条件1」と「条件2のド・ブロイ波」は量子の波動性を, 「条件2」と「条件3」は量子の粒子性を表現しており, これらすべてを満たす必要があります。

シュレディンガー方程式を導く大まかな流れは, 波が満たす一般的な波動方程式を導出し, 波動方程式に従う波動関数に条件2と3を満たすように変形していきます。

シュレディンガー方程式は波動関数 $\psi(x,t)$ についての方程式です。

シュレディンガー方程式の導出の出発点として, 波動関数が従う $\psi(x,t)$ 波動方程式を導きます。

ある弦を $xy$ 平面上で振動させたとき, 微小区間 $\Delta x (x, x+\Delta x)$ における $y$ 方向の運動方程式について考えてみましょう。

図中のA点, B点では張力 $S$ を受けるとします。

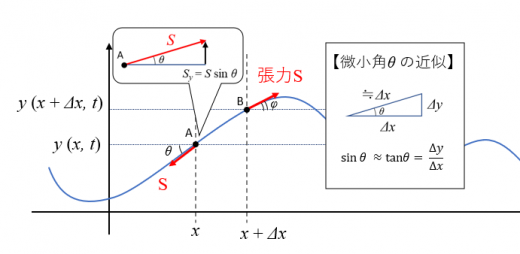
質量と加速度は以下のように表せます。

• 質量 $m$ ：線密度 $\rho$, 微小区間 $\Delta x$ の質量は $\rho \Delta x$

• 加速度 $a$ ：位置の変位 $y(x, t)$ を時間 $t$ で二階微分して$\dfrac{\partial^2{y(x,t)}}{\partial^2{t}}$

つまり, 運動方程式の左辺は

$$\text{左辺} = ma = \rho \Delta x \dfrac{\partial^2{y(x,t)}}{\partial^2{t}}$$

となります。

次に, 運動方程式の右辺（＝ どんな力が働いているか）を考えます。

微小区間 $\Delta x$ の張力の $y$ 成分の導出

A点における張力 $S$ の $y$ 成分 $S_{y,A}$ を考えると,

$$S_{y,A} = S \sin \theta\\$$

となります。弦の勾配（$\tan {\theta}$）は非常に小さいものとして, $\sin {\theta} \simeq \tan{\theta} = \dfrac{\Delta y}{\Delta x}$ で近似すると,

$$S_{y,A} = S \dfrac{\Delta y}{\Delta x} = S \dfrac{\partial{y}}{\partial{x}} (x,t)\\$$

となります。同様に, B点では $S_{y,B} = S \dfrac{\partial{y}}{\partial{x}} (x+\Delta x,t)$ になります。

微小区間 $\Delta x$ にかかる張力の $y$ 成分を $F$ とすると,

$$\begin{aligned} F &= S_{y,B} - S_{y,A} \\ &= S \dfrac{\partial{y}}{\partial{x}} (x+ \Delta x, t) - S \dfrac{\partial{y}}{\partial{x}} (x,t) \\ & = S \Delta x \dfrac{\partial^2{y(x,t)}}{\partial^2{x} } + O[(\Delta x)^2]　 \\ \end{aligned}$$

ここで, $y(x+\Delta x, t) = y(x, t) + \Delta y(x,t)$ を用いて,　第一項を展開しています。

$\Delta x \rightarrow 0$ とすると, $O[(\Delta x)^2]$ の項はゼロとみなすことができます。

※ $O[(\Delta x)^2]$ はオーダー記法を用いています。微小な量の扱いをするときにとても便利な記法です。

→オーダー記法の定義と大雑把な意味

※ここで用いられている $\dfrac{\partial{y(x, t)}}{\partial{x}}$ は偏微分を示しています。偏微分とは微分において一方の値を固定したまま,　微分を行う作業です。この場合, $y(x, t)$ において $t$ を固定し, $x$ で微分しています。

→偏微分の意味と計算例・応用

横波の波動方程式

以上から, 微小区間 $\Delta x$ でのy方向の運動方程式 $ma = F$ は次のようになります。

$$\begin{aligned} S \Delta x \dfrac{\partial^2{y(x,t)}}{\partial^2{x} } &= \rho \Delta x \dfrac{\partial^2{y(x,t)}}{\partial^2{t}} \\ \iff \dfrac{\partial^2{y(x,t)}}{\partial^2{x} } &= \dfrac{\rho}{S}\dfrac{\partial^2{y(x,t)}}{\partial^2{t}} \\ \end{aligned}$$

この式は弦を伝わる横波の波動方程式といいます。

波動方程式は運動方程式から導かれる, 波の運動を表す方程式であるとわかりますね。

波動方程式の一般解と定数 $c$ の意味

上記の波動方程式を満たす一般解は $$y(x,t) = f(x-ct) + g(x+ct)$$ と表されます。

$f(x-ct), g(x+ct)$ はそれぞれ $x, t$ を変数とする関数であり, どちらも $x$ と $t$ で二階微分可能な関数です。→上に凸，下に凸な関数と二階微分

$f(x-ct)$　を $x,t$ のそれぞれで二階微分することで示すことができます。

$$\begin{aligned} \dfrac{\partial^2{f(x-ct)}}{\partial^2{x} } &= f''(x-ct) \\ \dfrac{\partial^2{f(x-ct)}}{\partial^2{t} } &= c^2 f''(x-ct) \\ \end{aligned}$$

したがって, 波動関数

$$\dfrac{\partial^2{f(x-ct)}}{\partial^2{x} } = \dfrac{1}{c^2}\dfrac{\partial^2{f(x-ct)}}{\partial^2{t}}$$

が成立しています。

$g(x+ct)$ についても, 同様に波動関数が成立しています。

これらを線形結合した $y(x,t)$ は横波の波動関数の一般解を表します。

なぜ $c$ が横波の速さを示すのか？

ここで $f(x-ct)$ という関数について考えてみます。

$f(x-ct)$ は　$f(x)$ の $x$ に $x-ct$ を代入した関数とみなすことができます。

例えば, $y = A \cos{\dfrac{2 \pi}{\lambda}x}$ という正弦波の関数の $x$ に $x-ct$ を代入した式 $y = A \cos{\dfrac{2 \pi}{\lambda}(x-ct)}$ について考えます。

2つのグラフを比べると, $y = A \cos{\dfrac{2 \pi}{\lambda}(x-ct)}$　は, $y = A \cos{\dfrac{2 \pi}{\lambda}x}$ を $+x$ 方向に $\Delta x = ct$ だけ移動させた式であることがわかります。

$\Delta x = ct$ の両辺の次元（＝ 単位）が一致することから, $c$ が速度を示していることが理解できます。

また, $c$ の符号（向き）も重要で $f(x-ct)$ は $+x$ 方向, $g(x+ct)$ は $-x$ 方向へ進行する波を表現しています。

ここまでで波動方程式と, その解の波動関数について理解ができたと思います。

次回以降, 条件2と3を付与して波動関数を定めることで, シュレディンガー方程式を導出していきます。

シュレディンガー方程式の導出過程 -その2- へ続きます。