マクスウェル方程式

更新 2021/05/29

電磁気学の基本的な方程式である Maxwell（マクスウェル）方程式（maxwell equation）について，物理的意味を解説します。

Maxwell 方程式とは

Maxwell 方程式は電磁気学の基礎方程式です。基礎方程式とは文字通り基礎となる方程式のことで，たとえば力学の基礎方程式は Newton の運動方程式 $m\boldsymbol{a}=\boldsymbol{F}$ ，量子力学の基礎方程式としては Schrödinger 方程式 $i\hbar\dfrac{\partial{|\psi(t)\rangle}}{\partial{t}}=\hat{H}|\psi(t)\rangle$ が挙げられます。

本記事では Maxwell 方程式（maxwell equation）と記しますが，日本語ではマクスウェル方程式やマックスウェル方程式ともよばれます。個人的な体感ですが，マックスウェル方程式よりもマクスウェル方程式と書かれている文献の方が多いです。電磁方程式ともいいます。

電場 $\boldsymbol{E}(\boldsymbol{x},t)$ , 磁場 $\boldsymbol{B}(\boldsymbol{x},t)$ ，電荷密度 $\rho(\boldsymbol{x},t)$ ，電流密度 $\boldsymbol{j}(\boldsymbol{x},t)$ を用いて Maxwell 方程式は次のように書き表されます（これらの物理量については，電場・磁場・電荷密度・電流密度｜電磁気学における基本的な物理量を参照）。

Maxwell 方程式（微分形）

$\begin{aligned} \nabla\cdot\boldsymbol{\boldsymbol{E}} &=\dfrac{\rho}{\varepsilon_0} \\ \nabla\times\boldsymbol{\boldsymbol{E}} &=-\dfrac{\partial{\boldsymbol{B}}}{\partial{t}} \\ \nabla\cdot\boldsymbol{B} &=0 \\ \nabla\times\boldsymbol{B} &=\mu_0\boldsymbol{j} +\mu_0\varepsilon_0\dfrac{\partial{\boldsymbol{E}}}{\partial{t}} \end{aligned}$

Maxwell 方程式（積分形）

$\begin{aligned} \int_\text{S}\boldsymbol{E}\cdot\boldsymbol{n}\,d{S} &=\dfrac{1}{\varepsilon_0}\int_\text{V}\rho\,d{V}\\ \oint_\text{C}\boldsymbol{E}\cdot d{\boldsymbol{r}} &=-\dfrac{ d{}}{ d{t}}\int_\text{S}\boldsymbol{B}\cdot\boldsymbol{n}\, d{S}\\ \int_\text{S}\boldsymbol{B}\cdot\boldsymbol{n}\, d{S} &=0\\ \oint_\text{C}\boldsymbol{B}\cdot d{\boldsymbol{r}} &=\mu_0\int_\text{S} \boldsymbol{j}\cdot\boldsymbol{n}\, d{S} +\mu_0\varepsilon_0\dfrac{ d{}}{ d{t}}\int_\text{S}\boldsymbol{E}\cdot\boldsymbol{n}\, d{S} \end{aligned}$

実は，上で記したMaxwell 方程式の微分形と積分形は等価な式になっています。この等価性の証明については，マクスウェル方程式の積分形から微分形を導出するを参照してください。 Maxwell 方程式の４つの式は上から順にそれぞれ次の法則を表しています。

Gauss（ガウス）の法則
Faraday（ファラデー）の法則
磁場に対する Gauss の法則（磁荷非存在の法則）
Ampere-Maxwell（アンペール - マクスウェル）の法則

本記事では，積分形の物理的な意味を解釈することを試みます。ベクトル解析の発散・回転にあまり慣れていない読者にとっては積分形の方が直感的に理解しやすいと思います（発散・回転についてはベクトル場における発散（div）と回転（rot）の定義・意味を参照）。

【英語】姉は長年ペットを飼いたいと思っています。 My sister has wanted to have a pet 2

ろ過、蒸留、分留、クロマトグラフィー、ペーパークロマトグラフィー →分離ができる再結晶、昇華法 →分離と精製ができる 3

蒸留と分留の違いを教えてください。自分で調べてみたら、蒸留は液体と固体の混合物の分離で、分留は液体と液体の混合物の分離 4

円運動についてです。問題例: ある物体が半径10mの円周上を一定の速さで運動しており、その物体が一周するのに要する時間 5

Gauss の法則

Gauss（ガウス）の法則は積分形で次のように書き表されます。
Gauss の法則
∫SE⋅n dS=1ε0∫Vρ dV
    \int_\text{S}\boldsymbol{E}\cdot\boldsymbol{n}\, d{S}
    =\dfrac{1}{\varepsilon_0}\int_\text{V}\rho\, d{V}
    ∫S​E⋅ndS=ε0​1​∫V​ρdV
ε0\varepsilon_0ε0​ は真空の誘電率という正の定数で，ε0=8.85⋯×10−12 C/(Vm)\varepsilon_0=8.85\cdots\times10^{-12}\,\mathrm{C}/(\mathrm{V}\mathrm{m})ε0​=8.85⋯×10−12C/(Vm) で与えられます。
また，S\text{S}S は閉曲面で，閉曲面 S\text{S}S によって囲まれた領域を V\text{V}V としています。
既に流束・発散を学んだので，左辺が閉曲面 S\text{S}S を貫く電場 E\boldsymbol{E}E の流束・発散であることがわかると思います。右辺の積分は電荷密度を体積積分しているので，閉曲面 S\text{S}S 内の総電荷を表しています。
したがって Gauss の法則は，電荷が存在すると電場の発散が生じるということを意味します。正電荷であれば湧き出しが，負電荷であれば吸い込みが生じます。
例として正の点電荷 q>0q>0q>0 の場合を考えましょう。Coulomb（クーロン）の法則から，電場は点電荷から四方八方に広がるように作られます（静電気力とクーロンの法則）。実際に点電荷を囲むような閉曲面 C\text{C}C をとると，電場の流束が
    ∫SE⋅n dS=qε0>0
    \int_\text{S}\boldsymbol{E}\cdot\boldsymbol{n}\, dS
    =\frac{q}{\varepsilon_0}
    >0
    ∫S​E⋅ndS=ε0​q​>0
となり，電場の湧き出しが生じているということがわかります。

Faraday の法則

Gauss の法則では電荷の存在が電場を生むということを主張していました。Faraday の法則は，電場は磁場が時間変化することによっても生じるということを主張します。
Faraday（ファラデー）の法則は積分形で次のように書き表されます。
Faraday の法則
∮CE⋅dr=−ddt∫SB⋅n dS
    \oint_\text{C}\boldsymbol{E}\cdot d{\boldsymbol{r}}
    =-\dfrac{ d{}}{ d{t}}\int_\text{S}\boldsymbol{B}\cdot\boldsymbol{n}\, d{S}
    ∮C​E⋅dr=−dtd​∫S​B⋅ndS
ここで，C\text{C}C は閉曲線で反時計回りを正方向に取ります。S\text{S}S は閉曲線 C\text{C}C を縁に持つような曲面で，閉曲線の向きに応じて下図のように正の方向を決めます（右ねじが進む向き）。
左辺は閉曲線 C\text{C}C に沿った電場 E\boldsymbol{E}E の循環を表します。右辺の面積分は曲面 S\text{S}S を貫く磁場の流束を表しています。したがって Faraday の法則は，磁場が時間変化すると電場の循環が生じるということを意味します。逆に，磁場が時間変化しないとき，電場の循環が存在しないということです。
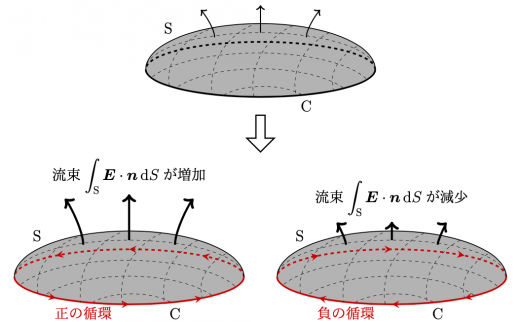
右辺には負符号が付いているので，磁場の流束が増加すると電場の負の循環が生じ，磁場の流束が減少すると電場の正の循環が生じます。

磁場に対する Gauss の法則

磁場に対する Gauss の法則は積分形で次のように書き表されます。
磁場に対する Gauss の法則
∫SB⋅n dS=0
    \int_\text{S}\boldsymbol{B}\cdot\boldsymbol{n}\, d{S}
    =0
    ∫S​B⋅ndS=0
電場の Gauss の法則と同様に，ここでも S\text{S}S は閉曲面です。
左辺は閉曲面 S\text{S}S を貫く磁場 B\boldsymbol{B}B の流束を表します。
すなわち磁場に対する Gauss の法則は，どんな閉曲面 S\text{S}S に対しても磁場の発散が存在しないことを意味します。電荷の存在が電場の発散を与えていましたから，磁場の発散を与えるような 磁荷（モノポール，磁気単極子）が存在しないという言い方もできます（その文脈で磁荷非存在の法則と呼ぶこともあります）。
簡単な例として棒磁石を考えましょう。棒磁石は磁場を作っていますが，棒磁石を囲むように閉曲面を取っても磁場の発散は存在しません（下図を見ると，Ｎ極側の正の発散とＳ局側の負の発散が打ち消し合うことがわかると思います）。棒磁石を断つように閉曲面を取っても同様に磁場の発散はありません（棒磁石の中にも磁場が存在することに注意してください）。
棒磁石にはＮ極とＳ極が存在して，Ｎ極とＳ極が引き合います。では棒磁石を半分に切るとどうなるでしょうか。Ｎ極とＳ極がバラバラの２種類ができると思う読者もいるかもしれませんが，実際にはＮ極とＳ極両方を持った磁石が２つできます。もしＮ極だけからなるような磁石があれば，それはまさにモノポールで，磁場に対する Gauss の法則が破られることになります。

Ampere-Maxwell の法則

もちろん，磁場の発散がないからといって磁場が存在しないわけではありません。磁場は循環として存在します。
Ampere-Maxwell（アンペール - マクスウェル）の法則は積分形で次のように書き表されます。
Ampere-Mawxell の法則
∮CB⋅dr=μ0∫Sj⋅n dS+μ0ε0ddt∫SE⋅n dS
    \oint_\text{C}\boldsymbol{B}\cdot d{\boldsymbol{r}}
    =\mu_0\int_\text{S} \boldsymbol{j}\cdot\boldsymbol{n}\, d{S}
    +\mu_0\varepsilon_0\dfrac{ d{}}{ d{t}}\int_\text{S}\boldsymbol{E}\cdot\boldsymbol{n}\, d{S}
    ∮C​B⋅dr=μ0​∫S​j⋅ndS+μ0​ε0​dtd​∫S​E⋅ndS
μ0\mu_0μ0​ は真空の透磁率という正の定数で，μ0=1.25⋯×10−6 N/A2\mu_0=1.25\cdots\times10^{-6}\,\mathrm{N}/\mathrm{A}^2μ0​=1.25⋯×10−6N/A2で与えられます（光速 ccc に対して ε0μ0c2=1\varepsilon_0\mu_0c^2=1ε0​μ0​c2=1 の関係があります）。
Faraday の法則と同様に，C\text{C}C は反時計回りを正とする閉曲線で，S\text{S}S は閉曲線 C\text{C}C を縁に持つような曲面です。流束の正の向きは右ねじの進む方向に取ります。
左辺は閉曲線 C\text{C}C に沿った磁場 B\boldsymbol{B}B の循環を表します。 右辺第１項の積分は電流密度の流束になっていますから，閉曲面 S\text{S}S を貫く電流を表します。また，右辺第２項の積分は閉曲面 S\text{S}S を貫く電場 E\boldsymbol{E}E の流束を表します。
したがって磁場を生じるものは２つあって，Ampere-Maxwell の法則は電流の存在や電場の発散の時間変化が磁場の循環を生じるということを表します。少し長いので電流と電場の発散の時間変化それぞれに対して見てみましょう。
電流によって磁場の循環が現れるという部分だけを切り取って Ampere の法則といいます。電流による磁場を Bj\boldsymbol{B}_{\boldsymbol{j}}Bj​ と書けば，次のように表現することもできます。
Ampere の法則
電流による磁場 Bj\boldsymbol{B}_{\boldsymbol{j}}Bj​ について，以下の式が成り立つ。
    ∮CBj⋅dr=μ0∫Sj⋅n dS
    \oint_\text{C}\boldsymbol{B}_{\boldsymbol{j}}\cdot d\boldsymbol{r}
    =\mu_0\int_\text{S}\boldsymbol{j}\cdot\boldsymbol{n}\, dS
    ∮C​Bj​⋅dr=μ0​∫S​j⋅ndS
電流が正のとき電流による磁場 Bj\boldsymbol{B}_{\boldsymbol{j}}Bj​ の循環も正，電流が負のとき磁場 Bj\boldsymbol{B}_{\boldsymbol{j}}Bj​ の循環は負になります。
Ampere-Maxwell の法則の第２項は Maxwell が付け加えた項で，電場 E\boldsymbol{E}E が時間変化するときには Ampere の法則だけでは不十分です。
電場が増えるとき磁場の正の循環を生じ，電場が減少するときには磁場の負の循環を生じます（Faraday の法則では負符号があったので逆でした）。
Ampere の項だけでは不十分であった背景には電荷保存則があります。電荷保存則は空間上に突然電荷がどこからともなく現れるということがないことを主張する法則です。電荷保存則については改めて別の記事に書くつもりです。

まとめ

以上で Maxwell 方程式の基本的な物理的意味がわかりました。

実際には，電荷密度 $\rho$ や電流密度 $\boldsymbol{j}$ が与えられているときに Maxwell 方程式を用いて電場 $\boldsymbol{E}$ と磁場 $\boldsymbol{B}$ の解を求めることになります（力学で力 $\boldsymbol{F}$ が与えられているときに運動方程式を用いて運動の解を求めることと同じです）。

物理を学ぶ際にはイメージがとても重要なので，Maxwell 方程式が何を意味しているか理解しておくことが大切です。

Maxwell 方程式さえあれば天地無双では？