マクスウェル方程式の積分形から微分形を導出する

更新日時 2021/05/29

マクスウェル方程式の記事でやり残していたことを証明したいと思います。積分形のマクスウェル方程式に対して，ガウスの発散定理，ストークスの定理を使って微分形を導出します。

マクスウェル方程式については，この記事をご覧ください。

ガウスの発散定理・ストークスの定理
Gauss の法則（微分形）の導出
Faraday の法則（微分形）の導出
磁場に対する Gauss の法則（微分形）導出
Ampere-Maxwell の法則（微分形）の導出

ガウスの発散定理・ストークスの定理

Maxwell 方程式の微分形を積分形から導出しようと思います。導出には Gauss の発散定理と Stokes の定理を用います（ガウスの発散定理・ストークスの定理の証明）。

Gaussの発散定理・Stokes の定理

ベクトル場 $\boldsymbol{A}$ に対して以下が成り立つ。

Gauss の発散定理： $\int_\text{S}\boldsymbol{A}\cdot\boldsymbol{n}\, d{S} =\int_\text{V}\nabla\cdot\boldsymbol{A}\, d{V}$ Stokes の定理： $\oint_\text{C}\boldsymbol{A}\cdot d{\boldsymbol{r}} =\int_\text{S}(\nabla\times\boldsymbol{A})\cdot\boldsymbol{n}\, d{S}$

Gauss の法則（微分形）の導出Gauss の法則は次の式で書き下されていました。
    ∫SE⋅n dS=1ε0∫Vρ dV
    \int_\text{S}\boldsymbol{E}\cdot\boldsymbol{n}\, d{S}
    =\dfrac{1}{\varepsilon_0}\int_\text{V}\rho\, d{V}
    ∫S​E⋅ndS=ε0​1​∫V​ρdV
左辺に Gauss の発散定理を用いると，
    ∫V∇⋅E dV=1ε0∫Vρ dV∫V∇⋅E dV=∫Vρε0 dV\begin{aligned}
    \int_\text{V}\nabla\cdot\boldsymbol{E}\, dV
    &=\dfrac{1}{\varepsilon_0}\int_\text{V}\rho\, d{V}\\
    \int_\text{V}\nabla\cdot\boldsymbol{E}\, dV
    &=\int_\text{V}\dfrac{\rho}{\varepsilon_0}\, d{V}
    \end{aligned}∫V​∇⋅EdV∫V​∇⋅EdV​=ε0​1​∫V​ρdV=∫V​ε0​ρ​dV​
となります。両辺はどちらも領域 V\text{V}V の体積積分になっていて，領域 V\text{V}V は任意に取ることができるので，局所的に
    ∇⋅E=ρε0
    \nabla\cdot\boldsymbol{E}
    =\dfrac{\rho}{\varepsilon_0}
    ∇⋅E=ε0​ρ​
が成り立ちます。∇⋅E\nabla\cdot\boldsymbol{E}∇⋅E が発散を表していることを知っていれば，電荷密度 ρ\rhoρ が電場の発散 ∇⋅E\nabla\cdot\boldsymbol{E}∇⋅E を与えるというように，直感的な理解ができると思います（ベクトル場における発散（div）と回転（rot）の定義・意味）。

この記事に関連するQ&A

1 こんにちは、これどうやって解けますか？僕は3番目の質問を解けませんです。解答用紙を読んだですが、まだ理解できない

2 物理科の方に質問をしたいです。写真の積分は自明でいいと思いますか？？たしかに微分方程式を解かずしてこの式を立てれるの

3 物理の原子分野のイオン化エネルギーについて分からないことがあります。「ちょっと一言」のとこの式がわかりません。イメージ

4 2-15´の式を2枚目の写真の式に変形する過程を教えてください

5 こんにちは、これどうやって溶けますか？僕解答用紙を読んだですが、まだ理解できない。

Faraday の法則（微分形）の導出Faraday の法則は次のように書き下されていました。
    ∮CE⋅dr=−ddt∫SB⋅n dS
    \oint_\text{C}\boldsymbol{E}\cdot d{\boldsymbol{r}}
    =-\dfrac{ d{}}{ d{t}}\int_\text{S}\boldsymbol{B}\cdot\boldsymbol{n}\, d{S}
    ∮C​E⋅dr=−dtd​∫S​B⋅ndS
左辺に Stokes の定理を適用すると，
    ∫S(∇×E)⋅n dS=−ddt∫SB⋅n dS∫S(∇×E)⋅n dS=∫S(−∂B∂t)⋅n dS\begin{aligned}
    \int_\text{S}(\nabla\times\boldsymbol{E})\cdot\boldsymbol{n}\, dS
    &=-\dfrac{ d{}}{ d{t}}\int_\text{S}\boldsymbol{B}\cdot\boldsymbol{n}\, d{S}\\
    \int_\text{S}(\nabla\times\boldsymbol{E})\cdot\boldsymbol{n}\, dS
    &=\int_\text{S}\left(-\dfrac{\mathrm{\partial}{\boldsymbol{B}}}{\mathrm{\partial}{t}}\right)\cdot\boldsymbol{n}\, d{S}
    \end{aligned}∫S​(∇×E)⋅ndS∫S​(∇×E)⋅ndS​=−dtd​∫S​B⋅ndS=∫S​(−∂t∂B​)⋅ndS​
となります。n\boldsymbol{n}n は時間に依存しないものとしました（閉曲線，閉曲面が時間変化するような場合にはこのような変形はできません）。また微分 −ddt-\dfrac{ d{}}{ dt}−dtd​ を積分の中に入れる際，被積分関数は x\boldsymbol{x}x に依存するので偏微分 −∂∂t-\dfrac{\mathrm{\partial}{}}{\mathrm{\partial}t}−∂t∂​ にしなければならないことに気をつけてください。
両辺はどちらも閉曲面 S\text{S}S における面積分になっていて，閉曲面 S\text{S}S や対応する法線ベクトル n\boldsymbol{n}n は任意に取れるので，局所的に
    ∇×E=−∂B∂t
    \nabla\times\boldsymbol{E}
    =-\dfrac{\mathrm{\partial}{\boldsymbol{B}}}{\mathrm{\partial}{t}}
    ∇×E=−∂t∂B​
が成り立ちます。この式も，∇×E\nabla\times\boldsymbol{E}∇×E が回転を表していることを知っていれば，磁場の時間変化 ∂B∂t\dfrac{\partial \boldsymbol{B}}{\partial t}∂t∂B​ が電場の回転 ∇×E\nabla\times\boldsymbol{E}∇×E を与えるという理解ができます（右辺に負符号があるので，回転が逆向きになることに注意します）。

磁場に対する Gauss の法則（微分形）導出

磁場に対する Gauss の法則は次のように書き下されていました。 $\int_\text{S}\boldsymbol{B}\cdot\boldsymbol{n}\, d{S} =0$ 電場の Gauss の法則のときと同様に，左辺に Gauss の発散定理を適用すると， $\int_\text{V}\nabla\cdot\boldsymbol{B}\, dV =0$ となります。領域 $\text{V}$ は任意に取れるので，局所的に $\nabla\cdot\boldsymbol{B} =0$ が成り立ちます。 $\nabla\cdot\boldsymbol{B}$ は磁場の発散なので，微分形も磁場の発散が存在しないことを意味しています。

Ampere-Maxwell の法則（微分形）の導出

Ampere-Maxwell の法則は次のように書き下されていました。 $\oint_\text{C}\boldsymbol{B}\cdot d{\boldsymbol{r}} =\mu_0\int_\text{S} \boldsymbol{j}\cdot\boldsymbol{n}\, d{S} +\mu_0\varepsilon_0\dfrac{ d{}}{ d{t}}\int_\text{S}\boldsymbol{E}\cdot\boldsymbol{n}\, d{S}$ Faraday 法則と同様に，左辺に Stokes の定理を適用すると， $\begin{aligned} \int_\text{S}(\nabla\times\boldsymbol{B})\cdot\boldsymbol{n}\, dS &=\mu_0\int_\text{S} \boldsymbol{j}\cdot\boldsymbol{n}\, d{S} +\mu_0\varepsilon_0\dfrac{ d{}}{ d{t}}\int_\text{S}\boldsymbol{E}\cdot\boldsymbol{n}\, d{S}\\ \int_\text{S}(\nabla\times\boldsymbol{B})\cdot\boldsymbol{n}\, dS &=\int_\text{S}\left(\mu_0\boldsymbol{j} +\mu_0\varepsilon_0\dfrac{\partial \boldsymbol{E}}{\partial t}\right)\cdot\boldsymbol{n}\, d{S} \end{aligned}$ となります。時間微分 $\dfrac{ d}{ d t}$ を中に入れる際， $\boldsymbol{E}(\boldsymbol{x},t)$ が $\boldsymbol{x}$ にも依存することに注意して時間偏微分 $\dfrac{\partial}{\partial t}$ に書き換えました。両辺の閉曲面 $\text{S}$ は任意に取れるので，局所的に $\nabla\times\boldsymbol{B} =\mu_0\boldsymbol{j} +\mu_0\varepsilon_0\dfrac{\partial \boldsymbol{E}}{\partial t}$ となります。 $\nabla\times\boldsymbol{B}$ は磁場の回転なので，磁場の回転が電流密度 $\boldsymbol{j}$ と電場の時間変化 $\dfrac{\partial \boldsymbol{E}}{\partial t}$ によって与えられることがわかります。

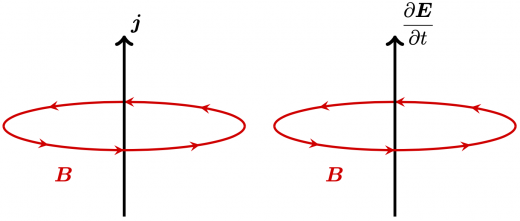
Ampere-Maxwell の法則（微分形）

電磁気学を終え，相対論等を扱うときに，微分形は大活躍するでしょう。