ケプラーの法則を導出する

第一法則については，別の記事ですでに証明が済んでいます→地球の公転軌道が楕円であることの導出。計算は少し大変ですが，ぜひ面倒くさがらず人生で一度は自分で計算してみると良いでしょう。ニュートン力学の原理の正しさを実感するための一つの重要な練習です。

この別記事での最後の楕円を表す式： $$r = \dfrac{1}{p} = \dfrac{\dfrac{mC^2}{K}}{1 + \dfrac{mC^2A}{K}\cos \theta}$$ について，$\lambda = \dfrac{mC^2}{K}, \varepsilon = \dfrac{mC^2A}{K}$ とおいて $$r = \dfrac{1}{p} = \dfrac{\lambda}{1 + \varepsilon\cos \theta}$$ として書き直します。以降はこの式で議論します。

太陽 $S$，もう一方の焦点 $F$，楕円の中心が $x$ 軸に乗っており，中心が原点 $O$ と重なるように，$xy$ 平面をとりなおします。楕円曲線と $x$ 軸との交点のうち，$S$ に近い方を $Q$，遠い方を $R$ とします。また，楕円曲線と $y$ 軸との交点の一方を $N$ と定義します。

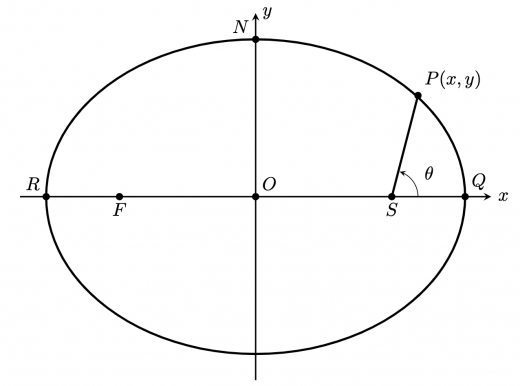
$P$が楕円曲線上を動く時，$\angle PSQ = \theta$ とおけば，惑星と太陽で成される線分の掃く面積は $$\Delta S = \dfrac{1}{2}r^2 \Delta \theta$$ よって， $$\begin{aligned} \therefore \dfrac{d{S}}{d{t}} = \dfrac{1}{2}r^2 \dot{\theta} = \dfrac{1}{2}h = \mathrm{const.} \end{aligned}$$ ただし，二次元極座標における運動方程式で $F_\theta = 0$ としているため，$r^2\dot{\theta}$ は定数でおけることに注意してください。

これはケプラーの第２法則「惑星の軌道運動の面積速度は常に一定である」に合致しています。この法則は「面積速度一定の法則」とも呼ばれます。

前節でつかった楕円を再掲します：

楕円曲線上の点 $P(x,y)$ をとります。このとき $$\begin{aligned} \overline{SQ} &= \dfrac{\lambda}{1+\varepsilon} \\ \overline{SR} &= \dfrac{\lambda}{1-\varepsilon} \end{aligned}$$ より， $$\overline{OQ} = \overline{OR} = \dfrac{1}{2}\overline{QR} = \dfrac{1}{2}(\overline{SQ} + \overline{SR}) = \dfrac{\lambda}{1-\varepsilon^2}$$ また， $$\begin{aligned} 2 \overline{NS} &= \overline{FQ} + \overline{SQ} = \overline{SQ} + \overline{SR} = \dfrac{2\lambda}{1-\varepsilon^2}\\ \overline{OS} &= \overline{OQ} - \overline{SQ} = \dfrac{\lambda}{1-\varepsilon^2} - \dfrac{\lambda}{1 + \varepsilon} = \dfrac{\lambda\varepsilon}{1 - \varepsilon^2}\\ \end{aligned}$$ これより， $$\overline{ON} = \sqrt{\overline{NS}^2 - \overline{OS}^2} = \dfrac{\lambda}{\sqrt{1-\varepsilon^2}}$$

これらを用いて楕円の面積と公転周期を求めていきます。

楕円の面積は $$S = \pi \left(\dfrac{\lambda}{1-\varepsilon^2}\right)\left(\dfrac{\lambda}{\sqrt{1-\varepsilon^2}}\right) = \dfrac{\pi\lambda^2}{(1-\varepsilon^2)^{3/2}}$$

また，公転周期は $$T = \dfrac{S}{\dfrac{d{S}}{d{t}}} = \dfrac{S}{h/2} = \dfrac{2\pi\lambda^2}{h(1-\varepsilon^2)^{3/2}} \\ \therefore T^2 = \left(\dfrac{2\pi\lambda^2}{h}\right)^2 \dfrac{1}{(1-\varepsilon^2)^3} = \dfrac{4\pi^2\lambda}{h^2}\overline{OQ}^3$$

これはケプラーの第３法則「惑星の公転周期の２乗は楕円の長径の３乗に比例する」に合致しています。これら３つの法則を合わせてKeplerの法則と呼びます。

これらの議論によって，「太陽を不動の質点，惑星を動く質点とみなせて，両者の間には万有引力のみが働く」と仮定すれば，Keplerの法則が導かれることを示せました。ニュートン力学の偉大さの再確認ができましたね。