ホイヘンスの原理

ホイヘンスの原理とは

ホイヘンスの原理は17世紀後半にオランダの物理学者ホイヘンス(Huygens)が発見した原理で, 波面の伝播と形成に関する非常に重要な原理です。

言葉だけではホイヘンスの原理の理解は難しいでしょう。

以下の図をみてください。

ある波源から波が広がっていく状況を考えましょう。ある時刻 $t$ で, 任意の波面を考えます。今は波の伝播・形成について考えているので, 次の瞬間 $t + \varDelta t$ での波面に興味があります。

ホイヘンスの原理は, この時刻 $t$ の波面上に無数の点波源があるとみなすことで次の瞬間 $t + \varDelta t$ での波面を導きます。

時刻が $t \to t + \varDelta t$ に移り変わる瞬間, それぞれの点波源から小さな球面状の波が出ると考えます。この波を素元波といいます。

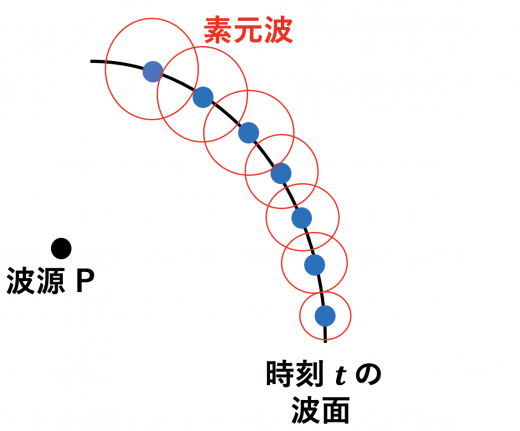
ホイヘンスの原理は, この素元波の「先端」をなめらかに繋ぐ包絡面が時刻 $t + \varDelta t$ での波面になると主張しているのです。

波は各時刻 $t$ において常にホイヘンスの原理に従いながら次の瞬間 $t + \varDelta t$ における波面を形成して伝播しています。

フレネルによる原理の修正

ホイヘンスの原理はホイヘンス=フレネルの原理と呼ばれることもあります。

ホイヘンスが主張した「ホイヘンスの原理」は理論的に完全ではなく, いくつかの不備がありました。1836年にフランスの物理学者フレネルが修正を加えたことによってホイヘンスの原理の問題点が解消されたので, フレネルの名を原理名に加えるという場合もあります。

ホイヘンスが提案した「ホイヘンスの原理」では、波が進行方向の前方に形成する波については明快に説明でき, 波の回折の現象もよく説明できるものでした。しかし, 素元波が後方に形成する包絡面が現れる時と現れない時があるという観測結果はうまく説明できなかったのです。

フレネルは波面は素元波の合成波として形成されると考えることによってこの問題を解決し, ホイヘンス＝フレネルの原理を完成させたのです。

こうした歴史的背景があり, 高校物理の範囲で単に「ホイヘンスの原理」というときには,フレネルによって修正が完了した「ホイヘンス=フレネルの原理」を指すことがほとんどです。こうした事情を誤解のないように理解しておきましょう。

水中の波の速度とホイヘンスの原理

海の波は海岸線に近づくと波面が海岸線に平行になっていくことが多いです。この現象をホイヘンスの原理に基づいて考えてみましょう。

素元波の様子を考えると, 水深が深い（海岸線から離れている）ほうが素元波の半径が大きい, すなわち波の伝わる速度が大きいことが予想できます。

実際に, 解析的に水中の波の速度 $v$ は $v \varpropto \sqrt{gh} \,$ ($g$ :重力加速度, $h$ :水深)となることが知られています。

このようにホイヘンスの原理は波の伝播や形成について重要な示唆を与えてくれるのです。

ホイヘンスの原理が活躍する場面

ホイヘンスの原理によって波動の最も基本的な性質の一つである「反射の法則」と「屈折の法則」を証明することができます。この証明については, 反射の法則と屈折の法則についてまとめた別の記事にて紹介します。→反射の法則・屈折の法則

また, ホイヘンスの原理をもとに考えると単スリットでの「波の干渉」という現象をより深く理解することができます。単スリットでの波の干渉についても別の記事で詳しく紹介します。