反射の法則・屈折の法則

反射の法則と屈折の法則についてそれぞれ説明します。

反射の法則は非常に単純明快で理解しやすいでしょう。

屈折の法則は目新しい式が登場して少し戸惑うかもしれません。理解するべき点は以下にまとめられます。

• 入射角と屈折角の $\sin$ の比が, 両媒質での速度・波長の比と一致する
• 屈折率の比は $n_1 \sin \theta_1 = n_2 \sin \theta_2$ が成り立つように定義されている。
• 領域1に対する領域2の屈折率は $n_{12} = \dfrac{n_2}{n_1}$ と定義されていて, $n_{12}$ と $1$ の大小を比較すると入射角 $\theta_1$ と屈折角 $\theta_2$ の大小関係がわかる。

図をみながら式の意味を正しく理解しましょう。

ホイヘンスの原理に基づくと, 「反射の法則」「屈折の法則」が成り立つ原理が明らかとなります。以下ではそれぞれの法則をホイヘンスの原理から証明します。

ホイヘンスの原理から反射の法則を証明します。

以下の図のように, 面に入射角 $\theta_1$ で入射する波を考えましょう。入射波１と入射波２は平行です。

波の進行方向と波面についての再確認です。以下の図のように, 入射波１の進行方向に対してその波面は垂直になっています。

反射する点 $\mathrm{A}$ を通る入射波１の波面は次のようになります。

Aを通る入射波１の波面と入射波２の交点を点 $\mathrm{C}$ としています。

それでは, 入射波１が面に到達した時刻を $t = 0$ として $t = 0$ の瞬間の波面を描いてみます。

$t = 0$ は入射波１が面に到達した時点なので, まだ入射波２は面に到達していません。

この後, 入射波１は反射し, 入射波２は点 $\mathrm{B}$ に直進します。

入射波２が点 $\mathrm{B}$ に到達する時刻を $t = t_1$ とします。$t = t_1$ にAを中心に広がった素元波（$\gets$ ホイヘンスの原理による）を描いてみましょう。

波の伝わる速さは入射波１・反射波・入射波２のいずれも等しい（ここでは $v$ とする）ので

• （素元波の半径） = $v t_1$
• $\mathrm{BC} = v t_1$

がいずれも成り立ちます。

この瞬間の点 $\mathrm{B}$ を通る反射波の波面を描いてみましょう。

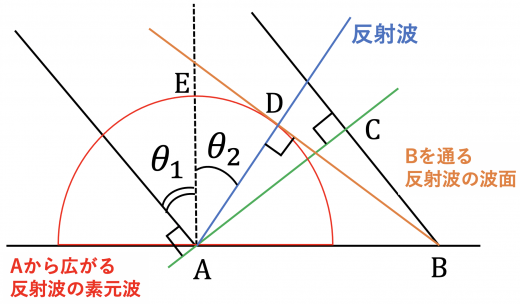
ここまでで証明の準備は整いました。二つの直角三角形 $\triangle ABC, \triangle BAD$ に注目しましょう。この二つの直角三角形が合同であることを示します。

まず斜辺について, 辺 $\mathrm{AB}$ は共通です。

底辺について

$$\mathrm{AD} = \text{（素元波の半径）} = v t_1 = \mathrm{BC}$$

がいずれも成り立ちます。

斜辺と他の一辺がそれぞれ等しいので

$$\triangle \mathrm{ABC} \equiv \triangle \mathrm{BAD}$$

が言えます。

このことから

• $\angle \mathrm{BAC} = 90^{\circ} - \angle \mathrm{CAE} = \theta_1$
• $\angle \mathrm{ABD} = 90^{\circ} - \angle \mathrm{BAD} = \theta_2$
• $\angle \mathrm{BAC} = \angle \mathrm{ABD}$

が成り立ちます。

したがって $\theta_1 = \theta_2$ （反射の法則）が成り立ちます。

同様の手続きで屈折の法則を証明しましょう。

入射波１が面に到達した時刻を $t = 0$ として, その瞬間の波面を描いてみます。

$t = 0$ の後, 入射波１は屈折し, 入射波２は点 $\mathrm{B}$ に直進します。

入射波２が点 $\mathrm{B}$ に到達する時刻を $t = t_1$ とします。$t = t_1$ にAを中心に広がった屈折波の素元波を描いてみましょう。

ここで波の伝わる速さに関して注意が必要です。

領域１で波の伝わる速さは $c_1$, 領域2で波の伝わる速さは $c_2$です。

媒質が異なれば, $c_1 \neq c_2$ です。ここでは $\mathrm{BC} = c_1 t_1$, 素元波の半径は $c_2 t_1$ です。

$t = t_1$ における点 $\mathrm{B}$ を通る屈折波の波面を描いてみましょう。

ここまでで証明の準備は整いました。

図の幾何学的な関係から

$$\begin{aligned} & \dfrac{\sin \theta_1}{\sin \theta_2} = \dfrac{\mathrm{BC}/ \mathrm{AB}}{\mathrm{AD}/ \mathrm{AB}} \\ &= \dfrac{\mathrm{BC}}{\mathrm{AD}} \\ &= \dfrac{c_1 t_1}{c_2 t_1} \\ &= \dfrac{c_1}{c_2} \\ &= \dfrac{f_1 \lambda_1}{f_2 \lambda_2} \\ &= \dfrac{f \lambda_1}{f \lambda_2} \\ &= \dfrac{\lambda_1}{\lambda_2} \end{aligned}$$

が成り立ちます。

また（絶対）屈折率は、真空中の光速 $c$ を媒質中の速度 $c_1$ (or $c_2$)で割った値として定義されています。

すなわち, それぞれ

$$n_1 = \dfrac{c}{c_1} \\ n_2 = \dfrac{c}{c_2} \\$$

と定義されています。

そのため $\dfrac{c_1}{c_2} = \dfrac{n_2}{n_1}$ が成り立ちます。

以上から, 屈折の法則が成り立ちます。

なお屈折の前後で波の振動数は変化しません。振動数は単位時間あたりに発せられた波の数と考えることができます。屈折は「違う媒質に進入して方向を変えるだけ」であり,その前後で波の数は変わりません。そのため, ここでは $f_1 = f_2 = f$ としました。

「$n_{12}$ について証明できていないのでは？」と思う方もいるかもしれません。

相対屈折率 $n_{12}$ は

$$\dfrac{n_2}{n_1} = n_{12}$$

が成り立つように定義されていると覚えましょう。定義なので証明方法はありません。

空気中から水中に屈折する場合, $n_{12} > 1$ なので $\theta_1 > \theta_2$ （入射角 $>$ 屈折角）になります。

一方で水中から空気中に屈折する場合, $n_{12} < 1$ なので $\theta_1 < \theta_2$ （入射角 $<$ 屈折角）になります。

なお, $n_{12} < 1$ の場合には「全反射」と呼ばれる現象によって屈折の様子が大きく変わる可能性があります。全反射については別の記事で詳しく解説します。