シュレディンガー方程式の導出過程とその意味 -その2-
シュレディンガー方程式の導出過程 -その1-で波動方程式と波動関数について解説しました。
これから, 波動方程式と波動関数について条件2と条件3を付与し, シュレディンガー方程式を導出していきます。
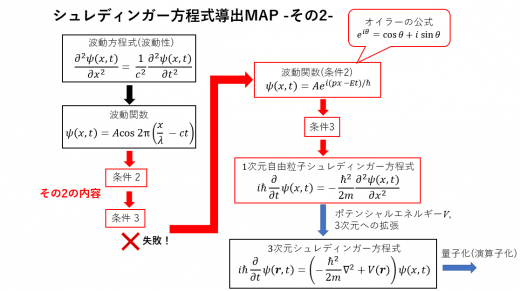
本記事(その2)では1次元シュレディンガー方程式の導出まで行います。
シュレディンガー方程式の導出過程では, 本記事が最も山場です。
波動関数の決定と電子の二重性
波動関数の決定と電子の二重性
まず, 前回導いた横波の波動方程式
を満たす波動関数 を 型の正弦波と仮定します。
この式を波動方程式の左辺, 右辺にそれぞれ代入してみましょう。
-
左辺
-
右辺
となります。
したがって, 波動関数 は
を満たすことがわかります。
波動関数 は 方向に進行する, 速度 , 波長 , 振動数 の正弦波を表します。
これより, 波動関数 を とします。量子力学では波動関数を で書く慣習があるためです。
波動関数
波動関数 は量子(電子)の状態を記述しています。
電子の二重性とデイラック定数
次に, この 型の波動関数に条件2を付与します。
条件2
-
ドブロイ方程式
-
波長とエネルギーの関係式
を に代入します。
ディラック定数 はエイチバーと読み,プランク定数 を用いて
で定義される。式を簡略化するためによく用いられる。
次に, 波動関数に条件3(エネルギー保存則)を付与します。
この記事に関連するQ&A
エネルギー保存則と複素数の導入
エネルギー保存則と複素数の導入
上記の波動関数 が
条件3
を満たすか考えます。波動関数
から条件3の と を抽出するために, 数学的なテクニックを用います。
- の抽出 → を で一階微分する
- の抽出 → を で二階微分する
の一階微分は 型であるのに対し, の二階微分は 型となるため, 両者を等号で結ぶことは困難です。
したがって, は 条件3: を満たさないため不適当な波動関数であることがわかりました。
つまり, 波動関数 を 型の正弦波
と仮定したことが誤りでした。
再び, 波動方程式を満たす波動関数から考えます。
複素数(オイラーの公式)とは
複素数(オイラーの公式)とは
先ほどの反省を生かし, 数学的側面から波動関数 について考えていきます。
条件3
を満たす波動関数について考えると, 時間 で一階微分した波動関数と, 位置 で二階微分した波動関数の形が一致する必要があります。 型や 型では不可能というわけです。
そこで, 複素数を導入し, オイラーの公式を使ってみます。
オイラーの公式はいくら微分をしても関数の形を変わらないという性質があります。
試しに とし で一階微分すると,
となり, 微分を繰り返すと, 係数がいくらか付きますが が残ります。
この関数を波動関数として用いれば, 条件3を満たすことができそうです。
電子の波動関数に複素関数を導入する
型の正弦波を仮定したときの波動関数
の形と, オイラーの公式を踏まえて, 以下のように新しい波動関数を定義します。
この式は波動方程式
を満たします。計算過程は省略しますが, 実際に のぞれぞれで微分して計算してみましょう。
複素共役の存在
今回, 複素数として, を選択しましたが, を用いて,
で考えても問題ありません。
と は互いに複素共役です。
どちらを選んでも物理的に同等なのは, 波動関数の本質は存在確率 にあるからです。
ちなみに, は 方向に運動量 で進む電子を意味しており, 反対に, の符号を変えた は 方向に進む電子を意味しています。
1次元自由粒子のシュレディンガー方程式の導出
1次元自由粒子のシュレディンガー方程式の導出
そして, 再びこの複素関数を用いた波動関数
が条件3 : を満たすか考えます。先ほどと同様に と で微分することで と を抽出します。
- の抽出 → を で一階微分する
両辺に, をかけると,
となります。
- の抽出 → を で二階微分する
両辺に をかけると,
となります。 の両辺に を作用させ,
2つの式を代入すると,
となります。
これで 「1次元の自由粒子のシュレディンガー方程式」が得られました。この式は条件1~3全てを満たした波動方程式となっています。
ポテンシャルを持たないことを自由粒子と表現したり, 束縛状態ということもあります。
ここまでで1次元シュレディンガー方程式の導出ができました。
ここからポテンシャルエネルギー(位置エネルギー)考慮し, さらには3次元への拡張を行います。
シュレディンガー方程式の意味について再度考えていきます。
シュレディンガー方程式の導出過程 -その3- へ続きます。










