ベクトル場の流束と循環
ベクトル場における流束,循環と呼ばれる量を定義します。定義とともに「イメージ」を大事にして学習しましょう。
これらの概念は電磁気学のボス「マクスウェル方程式」にも登場します。
この記事に関連するQ&A
ベクトル場の流束
ベクトル場の流束
ベクトル場について,面 を単位時間あたりに通過する量を流束といいます。
ベクトル場として流れ を考えます。ある断面 を(垂直に)単位時間あたりに通過する総流量を考えてみます。断面の法線ベクトルを とすると,微小面積 を通過する流量は と表されます(下図の円柱の体積が流量に対応します)。
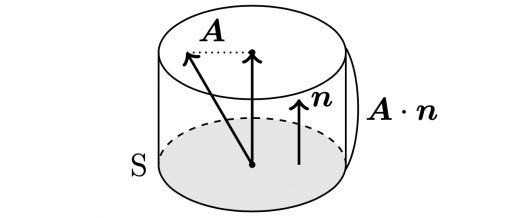
これを微小面積 を貫く の流束といいます。
微小ではなく一般の曲面 に対しても流束が定義できます。
ベクトル場 が曲面 を貫く流束 は以下のように与えられる。
つまり,微小面積の場合の流束を面全体で足し合わせれば良いということになります。ここで注意してほしいのは,法線ベクトル は曲面の上の各点で変化するということです。断面(平面)を考える際には法線ベクトル が面上で一定でしたが,曲面ではそうとは限りません。曲面上の各点で法線ベクトル が異なるので,面積素 それぞれに を対応させます(この意味で と書く方が理解しやすいかもしれません)。
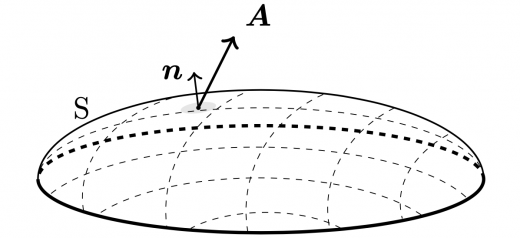
流束はベクトルがどの程度曲面を貫いているかを表しますから,たとえば球のような閉曲面(閉じた曲面)を考えると,曲面内からどれだけ「湧き出し」ているか,もしくは「吸い込み」があるかを表します(閉曲面を貫く流束を特に発散といいます)。

勘の良い読者は気づいているかもしれませんが,我々は既に一つ流束の例を知っています(→電場・磁場・電荷密度・電流密度|電磁気学における基本的な物理量を参照)。電流です。電流 は電流密度 の流束であるといえます( を電流密度 に置き換えると が電流 を与えることがわかると思います)。
他の例として熱流を挙げておきましょう。熱流の流束は熱がどれだけ移動しているかを表します。たとえば部屋の壁・床・天井を閉曲面にとると,夏は冷房を入れますので熱が外へ排出され,熱流の外向きの流束(発散)が正になります(湧き出し)。逆に冬は暖房を入れますので熱が中へ入り,熱流の外向きの流束(発散)が負になります(吸い込み)。流束の強さはどの程度熱の移動があるのかを表します。
ベクトル場の循環
ベクトル場の循環
ある閉曲線に沿ってどれだけ「渦巻いている」かを表す量を導入しましょう。
ベクトル場について,閉曲線 に沿った接線成分を足し合わせた(積分した)量を循環といいます。定義には線積分を用います→線積分の直感的意味・例題を使った計算方法の解説。
ベクトル場 の閉曲線 に沿った循環は以下のように与えられる。
どのようにしてこの式が出てくるのかもう少し見てみましょう。
閉曲線上 の各点で反時計回りになるように微小変位 を取ります。どれだけ「渦巻いている」かが知りたいので, がどの程度微小変位 に沿っているかという量を計算したいです。それが です。
が垂直であれば当然 となって が微小変位 に全く沿っていないということになりますし,同じ向きを向いていれば は大きな値に,逆向きであれば負の値になります。これを( をとても小さな に取り直して)足し合わせたものが周回積分になりますから,上の定義は確かにどれだけ「渦巻いている」かの量を与えるでしょう。
(ここでは反時計回りを正の循環に取りました。時計回りを正の循環に取っても,循環の正負が逆転するだけです。)

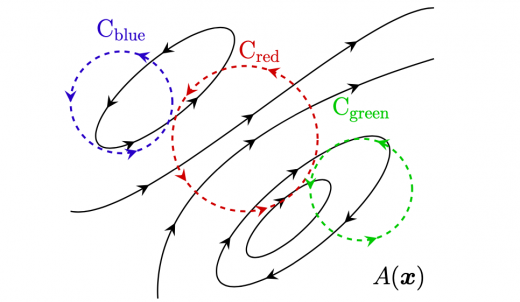
たとえば下図のようなベクトル場 と閉曲線 を考えましょう。 に沿った循環は正になりそうですし, に沿った循環は負になりそうです。一方で, に沿った循環の正負は見た目ではわかりそうにありません。
もっと物理的なイメージを与えましょう。ベクトル場を水の流れと思って,それぞれの閉曲線のような形の円形で中をくりぬいた落ち葉を浮かべることを考えましょう。 においた落ち葉はそれぞれ反時計回り,時計回りに回りそうですが, においた落ち葉はどちらに回転するのかわかりません。しかし, に沿った循環を計算すれば,落ち葉がどちらに回転するのかがわかるでしょう。
物理のコツは,数学とイメージの両方を常に意識しながら勉強することです。











