1次元箱型ポテンシャルの解

1次元の箱型ポテンシャルとは，以下のように図示できるポテンシャルのことです。

式で表すと以下のようになります。

$$\begin{aligned} V(x)= \begin{cases} 0 & (0 < x < a) \\ \infty & (x \leq 0, a \leq x) \end{cases} \end{aligned}$$

このポテンシャルは，古典的なイメージとしては「$x = 0$ と $x = a$ に高い壁があり，粒子はそこから外に出られない」状況を考えていることになります。

このポテンシャルが「(1次元の)箱」と呼ばれる理由を考えてみましょう。$V(x)$ の条件を3次元に拡張してみましょう。例えば以下のようなポテンシャルを考えてみます。

$$\begin{aligned} V'(x) = \begin{cases} 0 & (0 < x < a \, \text{かつ} \, 0 < y < b \, \text{かつ} \, 0< z < c) \\ \infty & (\text{上記以外}) \end{cases} \end{aligned}$$

3次元空間に図示してみると，このポテンシャルは，$0$ となっている領域が3辺の長さが$a, b, c$ の直方体となっていることがわかりますね。

つまり $V$ は，3次元に拡張すると箱型の領域となることから，1次元の箱と呼ばれているということです。

これ以降，簡単のため，$\int_{- \infty}^{\infty}dx$ は $\int dx$ と略記することにします。

ポテンシャルが $V(x)$ のときの波動関数を考えるために，エネルギーが時刻 $t$ によらず確定した値を取る状態，すなわち固有状態となる波動関数を求めていきましょう。

$V(x)$ は $t$ によらないので，定常状態におけるシュレディンガー方程式の一般解 で用いたように，波動関数 $\psi$ を $x$ の関数と $t$ の関数の積と考えて解を求めることができます。

$$\psi(x,t) = \phi(x) T(t)$$

以下では，この $\phi(x)$ を波動関数，固有関数，固有状態と読んで議論していきます。

$\phi(x)$ は以下のように時間に依存しないシュレディンガー方程式を満たしています。

$$\widehat{H} \phi = E \phi$$

$$\therefore \left(- \dfrac{\hbar^2}{2m} \dfrac{\partial^2}{\partial x^2} + V(x) \right) \phi = E \phi \tag{1}$$

ここで，$\phi$ には以下のようなような条件を課す事にします。

• $|\phi|^2$ は全領域で積分したときに正の有限の値を持つ。(＊)

• 全ての領域で恒等的に $0$ であるような解(自明な解)は考えない。(＊＊)

条件(＊)は波動関数を規格化できるようにしていることになります(波動関数の規格化については，詳しくは ボルンの確率解釈(確率規則) をご覧ください)。

これは，固有値 $E$ の固有関数 $\phi(x)$ に対し，$\psi(x,t) = \phi(x) \exp{\left (- \dfrac{i E t}{\hbar} \right)}$ となりますが，このとき

$$\begin{aligned} \int dx |\psi|^2 &= \int dx \psi^* \psi\\ &= \int dx \phi^* \exp{\left(\dfrac{i E t}{\hbar} \right)} \phi \exp{\left(- \dfrac{i E t}{\hbar} \right)} \\ &= \int dx \phi^* \phi = \int dx |\phi|^2 \end{aligned}$$

となるためです。

全ての領域で波動関数が恒等的に $0$ であるような解を考えるとき，$\int dx |\psi|^2 = 0$ となりますが，これはどこにも粒子の存在確率が存在しないことになるため不適とします。

ポテンシャルに応じて場合分けして，波動関数 $\phi$ を求めていきましょう。

箱の外側，つまり$x \leq 0, a \leq x$ での解の求め方を見ていきます。

(1)を変形すると

$$V(x) \phi = \dfrac{\hbar^2}{2m} \dfrac{\partial^2}{\partial x^2} \phi + E \phi \tag{1'}$$

いま，条件(＊)より，$\phi(x) = \infty$ という解は許されません。ゆえに $\phi$ は考えている領域で常に有限の値を持つことになります。ここで，箱の外側では，$V(x) = \infty$ であることを考えると，$\phi$ が $0$ でないような位置 $x$ に対し，(1’)の左辺は無限，右辺は有限となって矛盾します。

したがって，$x \leq 0, a \leq x$ では $\phi(x)$ は常に $0$ でなければなりません。

$$\phi(x) = 0$$

この結果より，ポテンシャル $V(x)$ が無限の値を持つ領域では，粒子は存在できないことがわかりました。

このあと箱の内側，つまり $0 < x < a$ での波動関数を求めていきますが，その前に波動関数の連続性について触れておきます。波動関数は考えている領域すべてでつながっている関数でなければなりません。今回考えているポテンシャルのかたち及び，その値が変わる領域が $x \leq 0, 0 < x < a, a \leq x$ と分かれていることから，それぞれでの領域での波動関数を $\phi_l, \phi_c, \phi_r$ とおくと

• 位置 $0, a$ で波動関数の値は等しい。すなわち

$$\phi_{l}(0) = \phi_{c}(0) \, , \phi_{c}(a) = \phi_{r}(a)$$

上記の条件は，境界条件あるいは接続条件などと呼ばれることもあります。

この条件を用いて，全領域で定義された波動関数を求めていくことになります。

箱の内側の解の求め方を見ていきましょう。

上で述べた波動関数の連続性より，

$$\phi(0) = 0 \, , \phi(a) = 0 \tag{2}$$

が成り立つことに注意します。

箱の内側では $V(x) = 0$ より，時間依存しないシュレディンガー方程式

$$-\dfrac{\hbar^2}{2m} \dfrac{\partial^2}{\partial x^2} \phi = E \phi$$

$$\therefore \dfrac{\partial^2}{\partial x^2} \phi = - \dfrac{2mE}{\hbar^2} \phi \tag{3}$$

が成り立ちます。

$E = 0$ のときは，境界条件により恒等的に $\phi(x) = 0$ となり，箱の外側の解と合わせると全ての領域で $\phi(x) = 0$ となります。これは条件(＊＊)に反するので，$E \neq 0$ と考えてよいことがわかります。

固有エネルギー $E$ の正負で場合分けしていきます。

エネルギーが負のとき

$E < 0$ のときを考えます。このとき，$E' = - E$ とおくと，$E' > 0$ であり，(3)式は

$$\begin{aligned} \dfrac{\partial^2}{\partial x^2} \phi &= - \dfrac{2mE}{\hbar^2} \phi \\ &= \dfrac{2mE'}{\hbar^2} \phi \\ &= \kappa^2 \phi \qquad (4) \end{aligned}$$

ただし，$\kappa$ は正の定数で

$$\kappa^2 = \dfrac{2mE'}{\hbar^2} \tag{5}$$

を満たしています。

微分方程式(4)の一般解は，$D_{+}, D_{-}$ を定数として

$$\phi(x) = D_{+} \exp{(\kappa x)} + D_{-} \exp{(- \kappa x)}$$

で与えられます(微分方程式(4)の解き方について，詳しくは 微分方程式の解法(同次形・線形微分方程式) をご覧ください)。ここで境界条件(2)を考えると

$$\phi(0) = D_{+} + D_{-} = 0$$

$$\therefore D_{-} = - D_{+} \tag{6}$$

$$\begin{aligned} \phi(a) &= D_{+} \exp{(\kappa a)} + D_{-} \exp{(- \kappa a)} \\ &= D_{+} (\exp{(\kappa a)} - \exp{(- \kappa a)}) \\ & = 2 D_{+} \sinh{(\kappa a)} \qquad (6') \end{aligned}$$

$\kappa > 0, a > 0$ より，$\sinh{(x)}$ のグラフを考えると (詳しくは 双曲線関数(sinh,cosh,tanh)の意味・性質・楽しい話題まとめ)，(6’)より

$$D_{+} = 0 \quad \therefore D_{+} = D_{-} = 0$$

これより許される解は

$$\phi(x) = 0$$

となりますが，これは条件(＊＊)に反します。

したがって，$E < 0$ のときは考えなくてよいことがわかりました。

エネルギーが正のとき

では $E > 0$ のときを考えていきます。(3)より，時間依存しないシュレディンガー方程式は

$$\begin{aligned} \dfrac{\partial^2}{\partial x^2} \phi &= - \dfrac{2mE}{\hbar^2} \phi \\ &= - k^2 \phi \tag{7} \end{aligned}$$

と変形できます。ここで，$k$ は正の定数で

$$k^2 = \dfrac{2mE}{\hbar^2} \quad \text{i.e.} \quad k = \dfrac{\sqrt{2mE}}{\hbar} \tag{8}$$

微分方程式(7)の一般解は

$$\phi(x) = S \sin{k x} + C \cos{k x} \tag{7'}$$

境界条件(2)を考えると

$$\phi(0) = C = 0 \quad \therefore C = 0 \tag{9}$$

$$\phi(a) = S \sin{ka} = 0 \tag{9'}$$

ここで，$S = 0$ とすると，自明な解となり，条件(＊＊)と反してしまいます。ゆえに，$S \neq 0$ として考えてよいことになります。よって，(9)から，$k$ について

$$\sin{ka} = 0$$

$$\therefore ka = n \pi \, (n \in \mathbb{N})$$

$$\therefore k = \dfrac{\sqrt{2mE}}{\hbar} = \dfrac{n \pi}{a} \tag{10}$$

が成り立ちます。 これより，取りうるエネルギー固有値 $E_n$ は

$$\dfrac{2mE}{\hbar^2} = \dfrac{n^2 \pi^2}{a^2}$$

$$\therefore E_n = \dfrac{\hbar^2 \pi^2}{2m a^2} n^2 \, (n \in \mathbb{N}) \tag{11}$$

と求められます。

この結果から，粒子の取りうるエネルギーが離散的に分布していることがわかります。また，このように粒子のエネルギーの分布が与えられたとき，最もエネルギーが小さい状態を基底状態，そうでない状態を励起状態と呼びます。

これより，$0 < x < a$ で固有状態となる波動関数の解は，$k_n = n \pi / a$ として

$$\phi(x) = S \sin{(k_n x)}$$

と求められます。

【補足】微分方程式(7)の解

微分方程式の解が(7’)のように表されることについて補足をしておきます。微分方程式(4)の解き方にならうと，(7)の解は $\alpha, \beta$ を定数として

$$\phi(x) = \alpha \exp{(i k x)} + \beta \exp{(-i k x)}$$

と表せます。ここで，オイラーの公式 (詳しくは オイラーの公式と複素指数関数) より

$$\exp{(i kx )} = \sin{k x} + \cos{k x}$$

$$\exp{(-ikx)} = - \sin{k x} + \cos{k x}$$

と表されるので，これを代入すると

$$\begin{aligned} \phi(x) & = \alpha (\sin{k x} + \cos{k x} ) + \beta (- \sin{k x} + \cos{k x})\\ &= (\alpha - \beta) \sin{k x} + (\alpha + \beta) \cos{k x} \end{aligned}$$

$\alpha - \beta, \alpha + \beta$ をそれぞれ $S, C$ とおけば，(7’)の表式が得られます。

(4)の解のように表しても，(7)の解のように表しても問題はありません。議論がしやすいようにかたちを選べば大丈夫です。

これより，全領域において，$n$ 番目の固有状態の波動関数 $\phi_n(x)$ は

$$\begin{aligned} \phi_n(x) = \begin{cases} S_n \sin{k_n x} = S_n \sin{\left(\dfrac{n \pi}{a} x \right)} & (0 < x < a) \quad (12-1)\\ 0 & (x \leq 0, a \leq x) \quad (12-2) \end{cases} \end{aligned}$$

と求められました。

規格化条件から定数を求める

条件(＊)により，$|\phi_n(x)|^2$ は全領域について積分したときに正の有限の値を持つとしてよいので，それを $1$ とする，すなわち規格化条件を課して $S_n$ を求めていきます。

$$\begin{aligned} \int_{- \infty}^{\infty} dx |\phi_n(x)|^2 &= \int_{0}^{a} dx |\phi_n(x)|^2\\ &= \int_{0}^{a} dx S_n^2 \sin^2{\left(\dfrac{n \pi}{a} x \right)} \\ &= S_n^2 \int_{0}^{a} dx \dfrac{1 - \cos{\left(\dfrac{2n \pi}{a} x \right)}}{2} \\ &= S_n^2 \left[\dfrac{1}{2}x - \dfrac{1}{2} \dfrac{a}{2 n \pi} \sin{\left(\dfrac{2n \pi}{a} x \right)} \right]_{0}^{a} \\ &= S_n^2 \dfrac{a}{2} = 1 \end{aligned}$$

ここで，波動関数としては存在確率や期待値が重要となりますが，これらの計算結果は $S_n$ の正負や共役がどちらであっても変わりません。なぜなら，存在確率や期待値の計算には，$S_n$ は $|S_n|^2$ のかたちで寄与するためです (期待値の計算については，量子力学における期待値)。 よって，簡単のために $S_n > 0$ とすると

$$S_n = \sqrt{\dfrac{2}{a}}$$

と求めることができます。$n$ によらない結果となりましたね。

概形の図示

$n = 1, 2, 3$ の場合において，$\phi_1, \phi_2, \phi_3$ 及び $|\phi_1|^2, |\phi_2|^2, |\phi_3|^2$ のかたちを具体的に求め，それをグラフで表してみましょう。$x \leq 0, a \leq x$ での $\phi_n$ はいずれも $0$ となるので，$0 < x < a$ での波動関数のかたちだけ考えれば十分ですね。この範囲では，上述より

$$\phi_n = \sqrt{\dfrac{2}{a}} \sin{\left(\dfrac{n \pi}{a} x \right)}$$

と書けるのでした。$n = 1, 2, 3$ をそれぞれ代入してみましょう。

$$\phi_1 = \sqrt{\dfrac{2}{a}} \sin{\left(\dfrac{\pi}{a} x \right)}$$

$$\phi_2 = \sqrt{\dfrac{2}{a}} \sin{\left(\dfrac{2 \pi}{a} x \right)}$$

$$\phi_3 = \sqrt{\dfrac{2}{a}} \sin{\left(\dfrac{3 \pi}{a} x \right)}$$

これらをそれぞれ図示してみましょう。

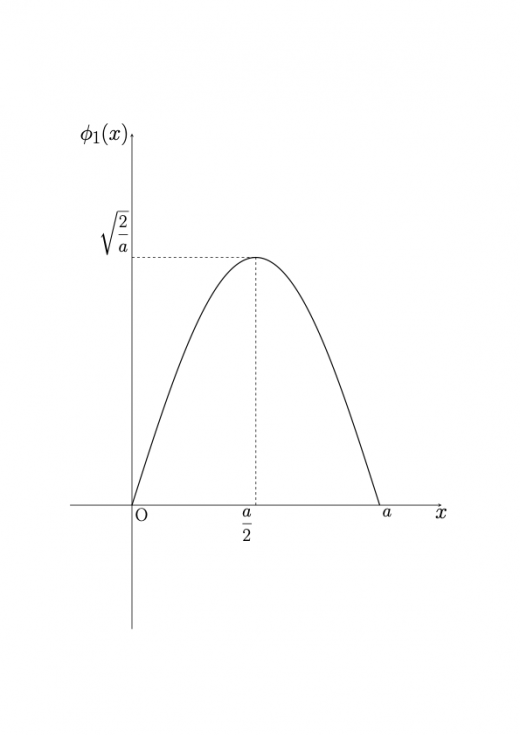
次に，これらを2乗してみましょう。

$$\begin{aligned} |\phi_n|^2 &= \dfrac{2}{a} \sin^2{\left(\dfrac{n \pi}{a} x \right)} \\ &= \dfrac{2}{a} \dfrac{1 - \cos{\dfrac{2 n \pi}{a} x}}{2} \\ &= \dfrac{1}{a} \left(1 - \cos{\dfrac{2 n \pi}{a} x} \right) \end{aligned}$$

となるので，

$$|\phi_1|^2 = \dfrac{1}{a} \left(1 - \cos{\dfrac{2 \pi}{a} x} \right)$$

$$|\phi_2|^2 = \dfrac{1}{a} \left(1 - \cos{\dfrac{4 \pi}{a} x} \right)$$

$$|\phi_3|^2 = \dfrac{1}{a} \left(1 - \cos{\dfrac{6 \pi}{a} x} \right)$$

となります。これらを図示してみましょう。

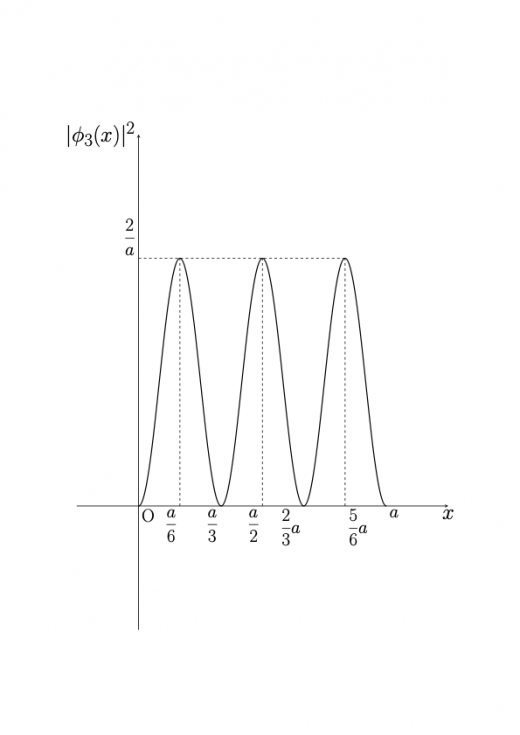
固有状態 $\phi_n$ に対する波動関数 $|\psi(x,t)|^2 = |\phi_n|^2$ は時刻 $t$，位置 $x$ での粒子の存在確率を表していることを思い出しましょう。この図を見ると，粒子の存在確率が高い地点がどこかがわかります。

この後一般解の時間発展について考えていきますが，その前に固有状態となる波動関数 $\phi_n$の直交性について議論しておきます。

$$\int dx \phi_n^* \phi_m = \int dx \phi_n \phi_m = \delta_{nm} \tag{A}$$

が成り立つことを示しましょう。ここで，$\delta_{nm}$ とはクロネッカーのデルタと呼ばれており，

$$\delta_{nm} = \begin{cases} 0 & (n \neq m) \\ 1 & (n = m) \end{cases}$$

である定数のことです。

まず $n \neq m$ のときは

$$\begin{aligned} \int dx \phi_n \phi_m = \dfrac{2}{a} \int_{0}^{a} dx \sin{\left(\dfrac{n \pi}{a} x \right)} \sin{\left(\dfrac{m \pi}{a} x \right)} \end{aligned}$$

ここで，三角関数の和と積の関係を思い出すと

$$\cos{\dfrac{(n-m) \pi}{a}x} = \cos{\dfrac{n \pi}{a}x} \cos{\dfrac{m \pi}{a}x} + \sin{\dfrac{n \pi}{a}x} \sin{\dfrac{m \pi}{a}x}$$

$$\cos{\dfrac{(n+m) \pi}{a}x} = \cos{\dfrac{n \pi}{a}x} \cos{\dfrac{m \pi}{a}x} - \sin{\dfrac{n \pi}{a}x} \sin{\dfrac{m \pi}{a}x}$$

より，

$$\sin{\dfrac{n \pi}{a}x} \sin{\dfrac{m \pi}{a}x} = \dfrac{1}{2} \left(\cos{\dfrac{(n-m) \pi}{a}x} - \cos{\dfrac{(n+m) \pi}{a}x} \right)$$

であることがわかります。したがって

$$\begin{aligned} \int dx \phi_n \phi_m &= \dfrac{2}{a} \int_{0}^{a} dx \dfrac{1}{2} \left(\cos{\dfrac{(n-m) \pi}{a}x} - \cos{\dfrac{(n+m) \pi}{a}x} \right) \\ &= \dfrac{1}{a} \left[\dfrac{a}{(n-m) \pi} \sin{\dfrac{(n-m) \pi}{a}x} - \dfrac{a}{(n+m) \pi} \sin{\dfrac{(n+m) \pi}{a}x} \right]_{0}^{a} \\ &= 0 \end{aligned}$$

となります。

続いて $n = m$ のときを考えます。このときは，波動関数に規格化条件を定めていることにより

$$\int dx \phi_n \phi_n = \int dx |\phi_n|^2 = 1$$

となります。したがって，(A)が成り立つことがわかりました。

時間に依存しないシュレディンガー方程式について，ポテンシャルが一般のかたちのときの一般解は，定常状態におけるシュレディンガー方程式の一般解 にて求めていました。

1次元の箱型ポテンシャルの一般解は，固有状態が(12-1)，(12-2)のように与えられたことより

$$\psi(x,t) = \displaystyle \sum_{n = 1}^{\infty} c_n \phi_n \exp{\left(- \dfrac{i E_n t}{\hbar} \right)} = \sqrt{\dfrac{2}{a}} \displaystyle \sum_{n = 1}^{\infty} c_n \sin{k_n x} \exp{\left(- \dfrac{i E_n t}{\hbar} \right)}$$

と求められます。この定数係数の性質を考えていきましょう。

規格化条件

この一般解 $\psi$ についても規格化条件が成り立っているとしたときの，定数係数どうしの関係を求めてみましょう。

$$\begin{aligned} \int dx |\psi|^2 &= \int dx \psi^* \psi\\ &= \int dx \left(\displaystyle \sum_{m = 1}^{\infty} c_m^* \phi_m^* \exp{\left(\dfrac{i E_m t}{\hbar} \right)} \right) \\ & \quad \cdot \left(\displaystyle \sum_{n = 1}^{\infty} c_n \phi_n \exp{\left(\dfrac{- i E_n t}{\hbar} \right)} \right) \end{aligned}$$

ここで，被積分関数について考えてみます。例として，$c_1^* \phi_1^* \exp{\left(\dfrac{i E_1 t}{\hbar} \right)} \left(\displaystyle \sum_{n = 1}^{\infty} c_n \phi_n \exp{\left(\dfrac{- i E_n t}{\hbar} \right)} \right)$ を計算してみましょう。上述した固有関数の直交性より $\phi_1^* \phi_n = \delta_{1n}$ となります。つまり，$\phi_1^*$ をかけると $\phi_n$ を持つ項しか残らないということです。よって

$$\begin{aligned} c_1^* \phi_1^* \exp{\left(\dfrac{i E_1 t}{\hbar} \right)} \left(\displaystyle \sum_{n = 1}^{\infty} c_n \phi_n \exp{\left(\dfrac{- i E_n t}{\hbar} \right)} \right) &= c_1^* \phi_1^* \exp{\left(\dfrac{i E_1 t}{\hbar} \right)} \\ & \quad \cdot c_1 \phi_1 \exp{\left(- \dfrac{i E_1 t}{\hbar} \right)} \\ &= |c_1|^2 |\phi_1|^2 \end{aligned}$$

同様に考えると，

$$\begin{aligned} c_2^* \phi_2^* \exp{\left(\dfrac{i E_2 t}{\hbar} \right)} \left(\displaystyle \sum_{n = 1}^{\infty} c_n \phi_n \exp{\left(\dfrac{- i E_n t}{\hbar} \right)} \right) = |c_2|^2 |\phi_2|^2 \end{aligned}$$

$$\begin{aligned} c_3^* \phi_3^* \exp{\left(\dfrac{i E_3 t}{\hbar} \right)} \left(\displaystyle \sum_{n = 1}^{\infty} c_n \phi_n \exp{\left(\dfrac{- i E_n t}{\hbar} \right)} \right) = |c_3|^2 |\phi_3|^2 \end{aligned}$$

$$\vdots$$

と計算することができることがわかります。これらを足し合わせることで，被積分関数は

$$\begin{aligned} \left(\displaystyle \sum_{m = 1}^{\infty} c_m^* \phi_m^* \exp{\left(\dfrac{i E_m t}{\hbar} \right)} \right) \cdot \left(\displaystyle \sum_{n = 1}^{\infty} c_n \phi_n \exp{\left(\dfrac{- i E_n t}{\hbar} \right)} \right) &= \displaystyle \sum_{n = 1}^{\infty} |c_n|^2 |\phi_n|^2 \end{aligned}$$

のように変形できます。したがって，波動関数が規格化されているとき，定数係数は

$$\begin{aligned} \int dx |\psi|^2 &= \int dx \sum_{n = 1}^{\infty} |c_n|^2 |\phi_n|^2 \\ &= \sum_{n = 1}^{\infty} |c_n|^2 \int dx |\phi_n|^2 \\ &= \sum_{n = 1}^{\infty} |c_n|^2 = 1 \end{aligned}$$

という関係を満たすことがわかりました。

初期条件から定数係数を求める

初期条件として，$t = 0$ では $\psi(x, 0) = f(x)$ であると考えます。$f(x)$ は，$x = 0, a$ での境界条件より

$$f(0) = 0, f(a) = 0$$

を満たしています。$f(x)$ を書き下すと

$$f(x) = \psi(x, 0) = \sum_{n = 1}^{\infty} c_n \phi_n$$

となります。この $f(x)$ に対し，

$$\begin{aligned} \int dx \phi_m^* f(x) &= \int dx \phi_m^* \sum_{n = 1}^{\infty} c_n \phi_n\\ &= \int dx \phi_m^* (c_m \phi_m) \\ &= c_m \end{aligned}$$

のように計算することで，定数係数 $c_m$ を求めることができます。つまり，固有関数 $\phi_1, \phi_2 , \, ... \, , \phi_n$ と，$t = 0$ での初期条件さえ分かれば，上記のようにして定数係数を求めることができるということになります。

これより，$f(x)$ を用いて $\psi$ を表すことができ，

$$\begin{aligned} \psi(x,t) &= \displaystyle \sum_{n = 1}^{\infty} \left(\int dx' \phi_n^* f(x') \right)\phi_n \exp{\left(- \dfrac{i E_n t}{\hbar} \right)} \\ &= \sqrt{\dfrac{2}{a}} \displaystyle \sum_{n = 1}^{\infty} \left[\int_{0}^{a} dx' \sin{\left(\dfrac{n \pi}{a} x' \right)} f(x') \right] \cdot \\ & \quad \sin{\left(\dfrac{n \pi}{a} x \right)} \exp{\left(- \dfrac{i E_n t}{\hbar} \right)} \end{aligned}$$

のようになります。

古典論との比較

箱型ポテンシャルにおける粒子の取りうるエネルギーに，古典力学と量子力学との違いが現れています。

古典力学では，箱型ポテンシャルに置かれた粒子は，ある1点で静止したままとどまるような解が許されます。このとき，粒子の持つエネルギーは $0$ となります。

一方，量子力学は，エネルギーが最も低い基底状態においても，そのエネルギーは

$$E_1 = \dfrac{\hbar^2 \pi^2}{2 m a^2}$$

と与えられ，$0$ にはならず有限の正の値になります。

エネルギーの期待値

エネルギーの期待値について，具体的な計算をしてみましょう。

期待値の定義より，エネルギーの期待値は

$$<\widehat{H}> = \int dx \psi^* \widehat{H} \psi$$

1次元箱型ポテンシャルにおける一般の状態の波動関数を代入し，エネルギーの期待値を求めてみましょう。シュレディンガー方程式より

$$i \hbar \dfrac{\partial}{\partial t} \psi = \widehat{H} \psi$$

が成り立っていることに注意します。

$$\psi = \displaystyle \sum_{n = 1}^{\infty} c_n \phi_n(x) \exp{\left(\dfrac{- i E_n t}{\hbar} \right)}$$

に対し

$$\begin{aligned} i \hbar \dfrac{\partial}{\partial t} \psi &= i \hbar \displaystyle \sum_{n = 1}^{\infty} c_n \phi_n(x) \left[ \dfrac{\partial}{\partial t} \exp{\left(\dfrac{- i E_n t}{\hbar} \right)} \right]\\ &= i \hbar \displaystyle \sum_{n = 1}^{\infty} c_n \phi_n(x) \left(- \dfrac{i E_n}{\hbar} \right) \exp{\left(\dfrac{- i E_n t}{\hbar} \right)} \\ &= \displaystyle \sum_{n = 1}^{\infty} E_n c_n \phi_n(x) \left(- \dfrac{i E_n}{\hbar} \right) \end{aligned}$$

と計算できるので，結局

$$\begin{aligned} <\widehat{H}> &= \int dx \psi^* \left(i \hbar \dfrac{\partial}{\partial t} \psi \right)\\ &= \int dx \left[\displaystyle \sum_{m = 1}^{\infty} c_m^* \phi_m^*(x) \exp{\left(\dfrac{i E_m t}{\hbar} \right)} \right] \left[\displaystyle \sum_{n = 1}^{\infty} E_n c_n \phi_n(x) \left(- \dfrac{i E_n}{\hbar} \right) \right] \\ &= \displaystyle \sum_{n = 1}^{\infty} |c_n|^2 E_n \int dx |\phi_n|^2 \\ &= \displaystyle \sum_{n = 1}^{\infty} |c_n|^2 E_n \end{aligned}$$

と求めることができます。