導体棒と誘導起電力
この記事では,動く導体棒を含む回路について扱います。まず,導体棒に生じる,ローレンツ力による誘導起電力を紹介した後,導体棒を含む回路についての,非常に有名で,重要な例題を紹介します。
この記事に関連するQ&A
ローレンツ力による導体棒の誘導起電力
ローレンツ力による導体棒の誘導起電力
磁場中で運動する導体には一般に誘導起電力が生じます。誘導起電力とは,電荷に対して仕事をし,電荷を偏らせる力のことです。 一般に,磁場中で運動する導体中の電荷はローレンツ力を受けます。その結果,電荷に対して仕事がなされ,電荷分布が偏ることになります。
ローレンツ力については,以下の記事を参照してください。
電場・磁場・電荷密度・電流密度|電磁気学における基本的な物理量

これから,導体棒中に生じる誘導起電力の向きと,大きさを導出します。上の図を見てください。今,図のように,磁場中で運動する導体を考えます。磁場の向きは青線で,速度の向きはグレーの線で表されています。この時,導体中の正電荷 は, のローレンツ力を受けます。正電荷は導体中に束縛されている(導体の外に出ることはない)ので,結局正電荷は導体と平行な成分のローレンツ力を受けて運動することになります。
導体棒の長さを とすると,この時正電荷は単位正電荷あたり, の仕事をされることになります。
十分時間が経って,電荷が偏ったとき,導体棒中に電位差が生じています。ローレンツ力とのつりあいを考えると,電位差 は, となることがわかります。
回路に電流が流れている状態などを考える場合,電荷の移動が完了した状態は存在しません。しかし,電荷は同様のローレンツ力を受けるので,結局 の電位差があると考えて計算して良いことになります。
特に導体棒と速度.磁場がそれぞれ直行している場合,
となります。大学入試などの問題では,このケースが多く見られます。
導体棒を含む回路の例題〜有名題〜
導体棒を含む回路の例題〜有名題〜
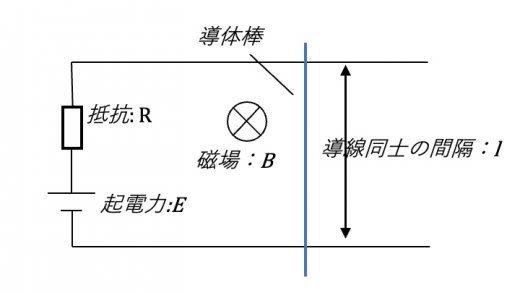 図のように,水平面上に2本の導体レールを間隔 で平行に置く。左端では,抵抗値 の抵抗と,起電力 の電池がある。また一様で時間変化のない,大きさ の磁場を紙面手前から奥の向きにかける。ここで,導体棒を図のように設置したところ,導体棒は運動を始めた。ここでは電流のつくる磁場は無視できるものとし,抵抗値 の抵抗以外で生じるエネルギー散逸(摩擦や抵抗など)は無視できるものとする。また図の左側を運動の正方向とする。
図のように,水平面上に2本の導体レールを間隔 で平行に置く。左端では,抵抗値 の抵抗と,起電力 の電池がある。また一様で時間変化のない,大きさ の磁場を紙面手前から奥の向きにかける。ここで,導体棒を図のように設置したところ,導体棒は運動を始めた。ここでは電流のつくる磁場は無視できるものとし,抵抗値 の抵抗以外で生じるエネルギー散逸(摩擦や抵抗など)は無視できるものとする。また図の左側を運動の正方向とする。
(1)導体棒の速さを とした時,導体棒に生じる誘導機電力を求めよ。
(2)回路に流れる電流の方向を適当に定め,キルヒホッフの法則にしてがって回路方程式を表せ。
(3)導体棒の運動方程式を表せ。
(4)十分時間が経った時,導体棒の速度は一定となった。この時の導体棒の速度を求めよ。

(1)前節で紹介した公式を用いて, となる。また,向きは を考えると,図の向きになる。
(2)図のように電流の向きを設定し,電流の大きさを とする。この時回路方程式は, となる。
(3)電流 が磁場から受ける力は一般に, である。この場合は向きは左側,大きさは なので,運動方程式は となる。
(4)十分時間が経った時,導体棒の速度は一定となったので, また,運動方程式にこれを代入すると, がわかる。これを回路方程式に代入すると, を得る。
キルヒホッフの法則については,以下の記事を参照してください。
(4)の別解〜微分方程式〜
前問において,回路方程式と運動方程式から, を消去してみます。すると, となります。この微分方程式は変数分離法で解くことができて, となります。ここで とすると, となることがわかります。導体棒の問題では,この形の微分方程式がよく出てきます。
変数分離法による微分方程式の解放については,以下の式を参照してください。
導体棒を含む回路の例題〜エネルギー収支〜
導体棒を含む回路の例題〜エネルギー収支〜
前問で導出した回路方程式と運動方程式について,エネルギー終始の式を導出し,それらを辺々足すことで,系全体のエネルギー収支を考察せよ。(回路方程式については両辺に を,運動方程式については両辺に をかけるとよい。)
回路方程式の両辺に をかけて を得る。
運動方程式の両辺に をかけて を得る。これら2式を辺々足すと, を得る。( の項が相殺されていることに注意)
左辺第1項は電池の仕事率,右辺第1項は抵抗で失われるジュール熱,右辺第2項は導体棒の運動エネルギーを表している。
磁場によるローレンツ力は速度と常に直行しているため,仕事をしない。従って, の項は消えている。
導体棒の問題は大学入試で頻出です。まず回路方程式と運動方程式をしっかり書くようにしましょう。











