キルヒホッフの法則の解説と例題

更新 2021/09/24

高校範囲の電磁気分野の中で大きなウエイトを占める，キルヒホッフの法則について説明します。例題の中でその応用法について説明します。

キルヒホッフの法則とは

キルヒホッフの法則とは，「キルヒホッフの第一法則」と「キルヒホッフの第二法則」の二つから構成される法則です。高校範囲の電磁気問題では，回路の問題を解く際に重要となってきます。

この問題の(1)番のDHを求める問題で、三角形DMAを切り出して、直線AMに垂直になるように、DHを降ろしていますが、 2

2022年慶応志木の問題です。大問▪️3の(2)番で、このような問題がありました。ここで図を書くと、添付図のようにな 3

問あなたの今の気持ちを伝える文を書こう。という問題に下記の様に答えを書きました。 ●Im glad that giv 4

エタノール（C2H5OH）の量論比での酸化反応式と理論空燃比を求めよ A) 化学反応式 B) 理論空燃比 5

キルヒホッフの第一法則

キルヒホッフの第一法則とは，根本的には電荷の保存則に関する法則です。言葉では以下のように表されます。
キルヒホッフの第一法則
回路内の各点において，その地点に入ってくる電流の総量と，その地点から出てくる電荷の総量は等しい。
∑ini=∑outi
\sum_{in} \boldsymbol{i} = \sum_{out} \boldsymbol{i}
in∑​i=out∑​i
これは，電荷と電気量保存の法則から容易に導かれます。
キルヒホッフの第一法則は，特に回路内の分岐点について用いると大きな効力を発揮します。具体的な回路の形で考えてみましょう。
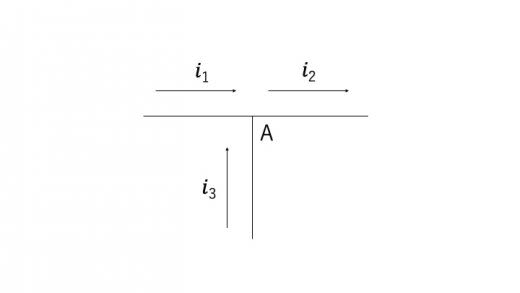
上図のような場合，点Aに関してキルヒホッフの第一法則を適用すると，
i1+i2=i3
i_1 + i_2 = i_3
i1​+i2​=i3​
となります。
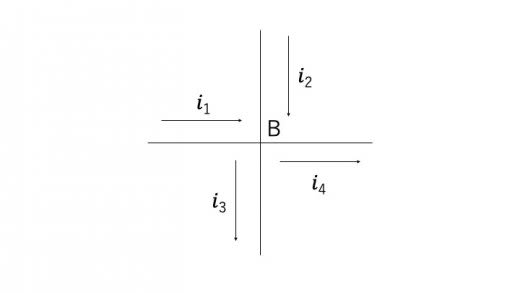
また，上図のような場合には，点Bに関してキルヒホッフの第一法則を適用すると
i1+i2=i3+i4
i_1 + i_2 = i_3 + i_4
i1​+i2​=i3​+i4​
となります。
キルヒホッフの第一法則を用いる場合には，電流が流れる方向が未知であったとしても，電流の向きを仮定することで適用することができます。実際の電流の向きと仮定した方向が正しければ正の値が，仮定した方向が誤っていれば負の値が得られることになります。

キルヒホッフの第二法則

キルヒホッフの第二法則は，キルヒホッフの電圧則とも呼ばれ，回路内の電位差に関する法則です。以下のように言語化することができます。

キルヒホッフの第二法則

どのような閉じた回路でおいても，その中での起電力の合計と電圧降下の値は等しくなる。

ここで，起電力とは，「電池などの外的な要因により電位が上昇すること」を指し，電圧降下とは，その名の通り「電圧が降下すること」を指します。この法則は，「どのような閉じた回路でも，その中での電位の変化は相殺される」ということ，言い換えれば，「電圧は上がったぶんだけ下がる」ということを表しています。

具体的な用い方は下の例題の際に確認してみます。

回路問題の解き方

回路の問題では，上で紹介したキルヒホッフの法則から回路内の電流の関係及び電位の関係を立式することが重要です。なお，このようにして立てた式を「回路方程式」と呼ぶこともあります。

例題からキルヒホッフの法則の用い方を確認してみましょう。

例題

下のような回路を考える。

AB間，BE間，CD間に流れている電流を求めよ。

以下のような解答が考えられます。

解答

AB間，BE間，CD間に流れている電流をそれぞれ $i_1$ ， $i_2$ ， $i_3$ とする。

まず，キルヒホッフの第一法則より

$i_1 = i_2 + i_3 \tag{1}$

さらに，回路ABEF，回路BCDEについてキルヒホッフの第二法則を用いて

$V = Ri_1 + 2Ri_2 \tag{2}$

$2Ri_2 = 3Ri_3 \tag{3}$

(3)より

$2i_2 = 3i_3$

$\therefore i_2 : i_3 = 3 : 2 \tag{3'}$

(1)と合わせて

$i_2 = \dfrac{3}{5} i_1 , i_3 = \dfrac{2}{5} i_{1} \tag{4}$

(2)に代入して

$V = Ri_1 + \dfrac{6}{5} Ri_1 = \dfrac{11}{5} R i_1$

$\therefore i_1 = \dfrac{5}{11} \dfrac{V}{R}$

(4)に代入して

$i_2 = \dfrac{3}{11} \dfrac{V}{R}, i_3 = \dfrac{2}{11} \dfrac{V}{R}$

これより，AB間，BE間，CD間に流れている電流は，それぞれ $\dfrac{5}{11} \dfrac{V}{R}$ ， $\dfrac{3}{11} \dfrac{V}{R}$ ， $\dfrac{2}{11} \dfrac{V}{R}$ である。

キルヒホッフの法則を用いると，回路の様子が面白いように明快に明らかになります。解けるようになるととても楽しいです。