オームの法則と抵抗の性質
オームの法則の公式,すなわち電圧と電流との間に比例関係があることを導き,そこから比例定数として電気抵抗が定義できることを確かめます。回路の問題での用い方や,簡単に抵抗率についても触れます。
オームの法則の導出
オームの法則の導出
オームの法則とは,わかりやすく述べると,電圧と電流の間には比例関係が成り立つという経験則です。その比例係数が抵抗値になります。オームの法則は下のような公式で表されます。
抵抗値 の抵抗に加わる電圧 ,流れる電流 の間には,
の関係が成り立つ。
オームの法則はあくまで経験則でしかありません。ただ,以下のような簡単なモデルでは,オームの法則が実際に理論的に成立していることを確かめることができます。このモデルでの議論を通じて,オームの法則は,経験則ではありますが,それほど突拍子もない法則であるわけでもないことがお分かりいただけると思います。
また,この法則をもって,「電気抵抗」とは何であるかのイメージを掴んでもらえれば良いと思います。
では,モデルを使った議論に移ります。下図のような,内部を電荷 の電子が移動する抵抗のモデルを考えることで,この公式を導出してみましょう。

計算のポイントは,電圧と電流は計算の途中で残しておくようにするということです。
上図の抵抗と電圧 の電池を繋いだ下図のような回路を考える。
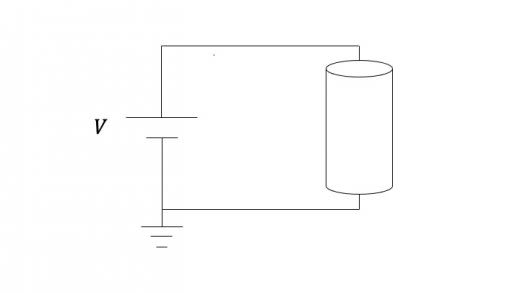
抵抗の電圧降下が電池の電圧と等しくなったとき,抵抗内の電場 および抵抗内を移動する電子の速度 は一定となる。
このとき,電場が一定であることより
が成り立つ。また,抵抗内の電子は等速運動をしているため,電子にはたらく力はつりあっていることになる。いま,電子には速度に比例する抵抗力がはたらいているとすると,力のつりあいより
また,電流 は単位時間あたりに流れる電荷であることを考えて(詳しくは別の記事で解説します)
(2)式より
(1)式と合わせて
また(3)式より
(1’)式,(3’)式を合わせて
これより,電圧 と電流 の間には比例関係があることが分かった。この比例定数を とおけば,
すなわちオームの法則が成り立つ。
この記事に関連するQ&A
抵抗についての考察
抵抗についての考察
オームの法則を導く過程で,私たちは抵抗値に関する次のような表式を得ました。
しかし,この式を導出する際には,抵抗の物理的な性質は用いていません。そこで,この式が私たちの直観的な抵抗のイメージ,つまり「抵抗値が大きいほど電流は流れにくく,逆に抵抗値が小さいほど電流は流れやすい」に合致しているか,確認してみましょう。
数密度と抵抗値の関係
(4)式によると,数密度と抵抗値は反比例の関係にあります。つまり,数密度が大きくなるほど抵抗値は小さくなるということです。これは下のような例を考えてみれば,定性的には正しいということが分かると思います。
ドミノ倒しの例を考えてみます。ドミノ同士の間隔を狭くすればするほど,短時間でより多くのドミノを倒すことができますね。いま,ドミノ同士の間隔を数密度,ドミノが倒れることを電流が流れることと考えれば,この例は数密度が小さいほど電流は流れやすく,したがって抵抗値は小さいということを表していることになります。
抵抗の長さと抵抗値の関係
(4)式によると,抵抗の長さと抵抗値は比例の関係,つまり抵抗が長いほど抵抗値は大きくなります。これも定性的には正しそうですね。なぜなら,抵抗が長いほど,電流が抵抗の端から端まで流れるには時間がかかることになるからです。
抵抗の底面積と抵抗値の関係
(4)式から,抵抗の底面積と抵抗値は反比例の関係,つまり抵抗の底面積が大きいほど抵抗値は小さいことになります。抵抗の底面積が大きいほど一度に移動することができる電荷の数は大きくなるので,流れる電流も大きくなりますから,この関係も定性的には正しいですね。
以上より,オームの法則を導出する際に得られた(4)式は,抵抗の物理的な性質を反映したものであるということができそうです。
回路におけるオームの法則
回路におけるオームの法則
回路において,オームの法則は,抵抗での電圧降下を説明する場合に用います。その際に重要なのは,抵抗のどちら側からどちら側へ電圧が降下するのかということです (抵抗のどちら側が電圧、つまり電位が大きいのかとも言い換えられます)。結論から言うと,電流の流れる向きに沿って電圧は降下します。例えば,下図のように電圧が流れているとすると,電圧は右側から左側へ降下します。

覚え方として,下図のように,回路に電流を矢印で書き,その矢尻に従って大きくV字を描く方法を紹介します。

緑で描かれた不等号の向きが,そのまま抵抗の両側の電圧の大小関係を示すことになります。
抵抗の単位と抵抗率
抵抗の単位と抵抗率
(4)式をもう一度書き下してみます。
抵抗の単位
抵抗の単位は [] で表され,オームと呼びます。これを国際単位系(SI)を用いて表すと,
これは(4)式から直接導くことができるので,計算問題としてやってみることをお勧めします。
抵抗率
詳細は別の記事にて説明しますが,抵抗率という概念について簡単に説明します。(4)式のうち, の部分は抵抗の形状によって決まりますが, の部分は抵抗の材質などによって決まります。この因子を抵抗率 として定義します。
抵抗率の単位は[]となります。
抵抗値の表式が,導出過程では抵抗の物理的性質を用いていないのに,それを定性的に含意しているところが面白いですね。










