静電エネルギーの定義・公式|コンデンサー・球・球殻
静電エネルギーの定義について紹介するとともに,具体的な場合における公式を導出します。
静電エネルギーの定義
静電エネルギーの定義
静電エネルギーとは,端的に言えば「クーロン力による位置エネルギー」のことです。もちろん単位は[J]:ジュールとなります。クーロン力が保存力(詳しくは位置エネルギーの定義と例(重力・弾性力・クーロン力)を参照) であることを考えれば,これは,「ある電荷が基準点から今の位置まで,クーロン力に逆らってゆっくりと移動した時にされた仕事…(*)」と同値であると考えることができます。
複数の電荷,即ち電荷分布に対しても静電エネルギーを考えることができます。この時の静電エネルギーも,電荷が一つである場合と同様に,その電荷分布を形成するすべての電荷が,基準点から現在の分布を形成するまでに必要な仕事のことと考えることで求めることができます。
具体的な静電エネルギーの表式の求め方としては,(*)を用いると考えやすいです。(*)を用いて,3つの例について,静電エネルギーの式を計算して求めてみましょう。
この記事に関連するQ&A
平行平板コンデンサーの静電エネルギー
平行平板コンデンサーの静電エネルギー
高校物理の範囲では,平行平板コンデンサーが蓄える静電エネルギーが最も重要となります。
下図のように,面積 ,極板間隔 の平行平板コンデンサーの上下に,それぞれ の電荷が一様に分布しているときを考えます。

このコンデンサーが蓄える静電エネルギー は
となります。
平行平板コンデンサーが蓄える静電エネルギーは,回路の計算問題では頻繁に使うことになります。求め方と同時に,この表式自体も公式として覚えておくことをお勧めします。
コンデンサーの理論 で扱ったように,極板上の面電荷密度 ,極板間の電場 ,極板間の電圧 ,電気容量 は,それぞれ
である。
いま,充電の途中,極板上の電荷の絶対値が になったときの電圧 は,
であり、ここからさらに だけ電荷を蓄えるために必要な仕事 は
を から まで積分して,求める静電エネルギー は
となる。
コンデンサーの公式
を用いれば,他の表式も得られる。
一様に帯電した球の静電エネルギー
一様に帯電した球の静電エネルギー
下図のように,半径 の球に大きさ の電荷が一様に帯電している場合を考えます。
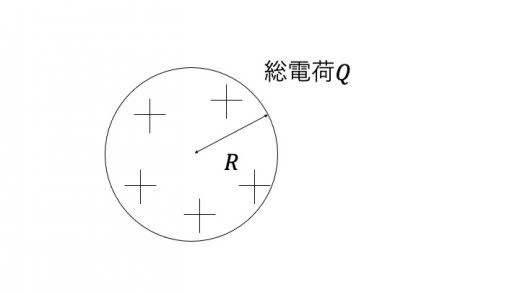
この球が持つ静電エネルギー は,
と表されます。
証明に移る前に,一様に帯電した球の静電ポテンシャル が,球の外側ではどのように書けるかを導いておきましょう。簡単のため,基準点は無限遠とします。
半径 の球Bに大きさ の電荷が一様に帯電している場合を考える。座標の原点を球の中心 に取り,原点からの距離を で表すことにする。
ここでは のときのみを示す。
中心を とする半径 の球B’を考える。この球が空間内に占める領域を ,この球の表面積を とすると,Gaussの法則 (詳しくはマクスウェル方程式内の「Gaussの法則」の節を参照ください) により,
左辺は,各電荷は放射状に電場を放出することを考えれば,B’の表面の各地点においても電場は表面と直交している。 より
であるから,
一方,右辺の積分はいま領域 内の総電荷を求めることに等しく,
よって,
よって,
これは の場合も成立している。
この結果より,一様に帯電している球の電場は,その外側では,帯電している全電荷が球の原点に集まっているときと同じ表式になっていることが分かる(詳しくは別の記事で説明します)。
したがって, でのこの球による静電ポテンシャル は,電位の定義|エネルギーとしての解釈・具体例のときと同様に計算して,
となる。
これを用いて,一様に帯電した球が持つ静電エネルギーを求めてみましょう。
下図のように,電荷密度 ,半径 の球の半径を だけ拡大することを考える。ただし,
とする。

新たに拡大する範囲に含まれる電荷は
であることに注意する。
いま、半径 の球に含まれる電荷 は
であり、この電荷が の位置に作る静電ポテンシャル は,上で求めたように
であるから,厚さ ,全電荷 の球殻状電荷を付け加えるために必要な仕事 は,仕事の定義により
である。これを から まで積分して,
を得る。
一様に帯電した球殻の静電エネルギー
一様に帯電した球殻の静電エネルギー
下図のように,半径 の球殻に電荷 が一様に帯電している場合を考えます。

このとき,球殻が持つ静電エネルギー は
と表されます。
基本となる考え方は導体球の場合と同様ですが,球殻の場合は中身が詰まっていないことに注意してください。
まず,一様に帯電している球殻の静電ポテンシャルは,その外側においては,一様に帯電した球の場合と同様に考えれば,同じ表式になることが分かります。
では、この時電荷分布はどのようになっているでしょうか (電荷分布について考えるのは、それさえ分かってしまえば、マクスウェル方程式 により、理論上は必要な物理量を全て求めることが可能となるからです)。これについては,静電誘導を考慮することにより求めることができます。
導体の球殻を帯電させると,電気誘導により,電荷は導体表面にのみ分布することに注意する。
いま,下図のように,半径 の球殻に全電荷 が蓄えられている状態で,電荷をさらに だけ付加することを考える。

全電荷が である時、球殻の持つ静電ポテンシャル は,先程と同様に求めて
微小電荷 を付加するために必要な仕事 は
であるから,球殻に蓄えられる全電荷が のとき,その球が蓄える静電エネルギーは, を から まで積分して
となる。
電池のする仕事と静電エネルギー
電池のする仕事と静電エネルギー
高校物理で見落としがちになってしまうのが,電池がする仕事とコンデンサーが蓄える静電エネルギーとの関係です。この二者の関係を,次の例題について確認してみましょう。
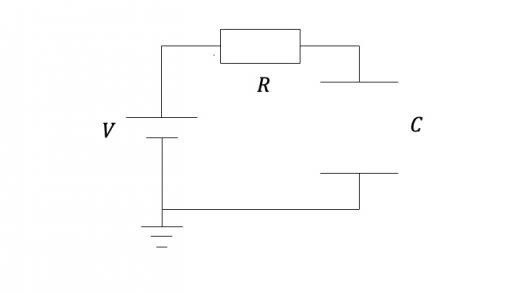
下図のように,電圧 の電池,抵抗値 の抵抗,および静電容量 のコンデンサーを繋いだ回路を考える。十分時間が経ったとき,
(1)電池がした仕事 を求めよ。
(2)コンデンサーが蓄えている静電エネルギー を求めよ。
(3)抵抗において消費されたジュール熱の総和を求めよ。
問題文中に「十分時間が経ったとき」とあることに注目します。高校物理では,十分時間が経ったときというのは,それ以上着目している系の内部の物理量が変化しない状態,即ち定常状態になったことを表します。
ここで,このようなコンデンサーを含む回路の定常状態の考察のポイントを一つ紹介します。
定常状態になったとき,回路のコンデンサーを含んでループになっている部分には,電流は流れていない。
もし定常状態でありながら,回路のコンデンサーを含む部分に電流が流れているとすると,そこには電荷の移動が生じていることになり,コンデンサーが蓄えている電荷の総量も変化することになります。これはコンデンサーが定常状態にあることに反するため,上記の事実が成立していることがわかります。
また,(3)については,抵抗で消費されるジュール熱の公式はありますが,今回のような問題では抵抗を流れる電流や抵抗に加わる電圧は時々刻々と変化し,それを追うのはそれなりに面倒なので,ジュール熱の公式を利用して解こうとするとかなり骨を折ることになります。このような場合では,熱がエネルギーの一つの形態であることを利用して,熱力学第一法則(エネルギー保存則)から求めることを考えてみましょう。
それでは解答に移ります。
(1) 十分時間が経ったとき,即ち定常状態において,コンデンサーに蓄えられている電荷 を求める。定常状態では回路に電流が流れていないことに注意して,キルヒホッフ則 (詳しくは別の記事で解説します) より
これより,電池は電荷量 の電荷を静電ポテンシャルが だけ高いところに押し上げたので,電池がした仕事は,
(2)キルヒホッフ則より,定常状態ではコンデンサーに加わっている電圧は であるから,コンデンサーの静電エネルギーの公式より,
(3)抵抗で消費されるジュール熱の公式はありますが,今回のような問題では抵抗を流れる電流や抵抗に加わる電圧は時々刻々と変化し,それを追うのはそれなりに面倒なので,ジュール熱の公式を利用して解こうとするとかなり骨を折ることになります。このような場合では,熱がエネルギーの一つの形態であることを利用して,熱力学第一法則(エネルギー保存則)から求めることを考えてみましょう。
(1)と(2)の結果より,
であることがわかる。ここで,抵抗,コンデンサーおよび導線を系の内部,電池を系の外部と考えて,この系に対して熱力学第一法則 (詳しくは熱力学第一法則|仕事と内部エネルギーの関係をご覧ください) を用いると,
ここに, は一般に,系の内部で発生した熱である。いま,抵抗,コンデンサーおよび導線を系とみなしているので, は導線により生じるジュール熱であると認めてよい。(1)と(2)の結果より,定常状態になるまでに抵抗で消費されたジュール熱の総和は
電池とコンデンサーを含むより一般の回路についても,電池のした仕事は全てコンデンサーに蓄えられるわけではなく,一部はジュール熱として消費されてしまいます。ですので,回路の問題で、エネルギー収支の観点から「あれ,おかしいことが起きてるぞ」となってしまっても,一旦冷静になって,ジュール熱を考えられているかどうか確かめてみてください。
余談になりますが,熱力学第一法則は,気体が関わっていなくても,一般のエネルギーの関係を論じることに使えます。この普遍性こそが熱力学の魅力でもありますね。











