コンデンサーの理論

図のように，面密度 $\sigma$，$-\sigma$ に帯電している2枚の金属平板を考える。

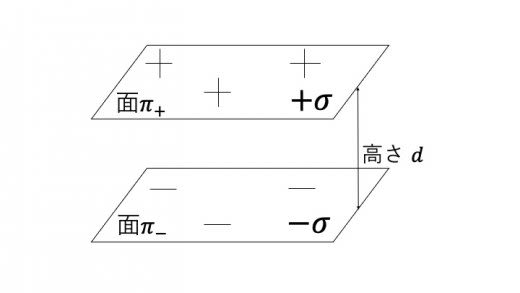
正に帯電している平板から発生する電場を求める。図のような円柱領域を $V$，その表面を $D$ とする。

Maxwell方程式より，

$$\int_{D} E \cdot n dS = \dfrac{1}{\varepsilon _0} \int_{V} \rho dV$$

今，対称性により，平板の上下で電場の大きさは等しいから，

$$(\text{左辺}) = ES + ES = 2ES$$

また，円柱領域内部の電荷を考えることにより，

$$(\text{右辺}) = \dfrac{\sigma S}{\varepsilon_0}$$

$$\therefore E = \dfrac{\sigma}{2 \varepsilon_0}$$

負に帯電している電場の大きさもこれと等しい。電荷の正負に注意して，この2枚の平板間の電圧を求める。2枚の平板が距離 $d$ だけ離れている時，

$$V = \int_C E \cdot dr \\ = 2Ed \\ = \dfrac{\sigma}{\varepsilon_0} d$$

コンデンサーは2枚の平板が有限の大きさを持ったものとみなせる。その時，平板の面積を改めて $S$ とおくと，

$$V = \dfrac{\sigma S}{\varepsilon_0} d \dfrac{1}{S} \\ =Q \dfrac{d}{\varepsilon_0 S}$$

$$\therefore Q =\dfrac{\varepsilon_0 S}{d} V$$

比例定数を電気容量 $C$ と置き直せば，

$$Q =CV$$

を得る。$\blacksquare$

平行版コンデンサーの形状は公式1の証明と同様とする。正に帯電している極板は，負に帯電している極板から電場

$$E_{-} = \dfrac{Q}{2 \varepsilon_0 S} =\dfrac{1}{2} E$$

により引き寄せられている。正に帯電している極板が持つ電荷は $Q$ であったから，ローレンツ力を考えれば極板間引力は

$$F = Q E_{-} = \dfrac{1}{2} Q E = \dfrac{1}{2} \dfrac{Q^2}{\varepsilon_0 S}$$

となる。対称性により，負に帯電している平板が正に帯電している平板から受ける力も上と同じ式で表される。$\blacksquare$