フレミングの左手の法則の復習・理論的解説｜電磁力の定義｜中学から高校まで

磁場中に導体をおき，その導体に電流を流すと，導体は磁場から力を受けます。この力を電磁力と呼びます。この力の向きの覚え方として，フレミングが考え出したフレミングの左手の法則があります。下図のように左手を配置すると，親指が電流，人差し指が磁場，中指が電磁力の向きと一致します。

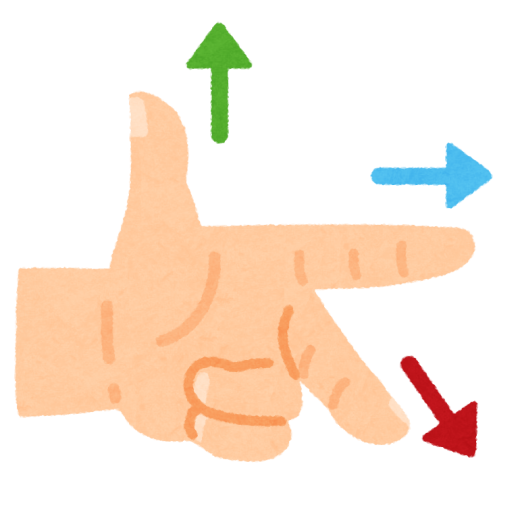
親指から順に「電・磁・力」と覚えると覚えやすいと思います (画像についてはいらすとや様よりお借りいたしました)。

高校物理以上になると，電磁力を数式で表せるようになります。

ここで用いられている用いられている $\times$ という記号は外積を表しています。外積については，詳しくは 内積と外積の意味と嬉しさ をご覧ください。

高校物理で頻出の，直線電流による磁場についての公式を，Maxwell方程式より導出してみましょう。

導出の前に，静磁場についてのについてのMaxwell方程式を確認しておきます。

Maxwell方程式の微分形については マクスウェル方程式 を，Maxwell方程式の積分形については マクスウェル方程式の積分形から微分形を導出する をご覧ください。

下図のような一定の大きさの直線電流の周りに発生する磁場を求めてみましょう。

磁場を円Cの半径方向に平行な方向の成分 $B_r$，円Cの半径方向に垂直な方向の成分 $B_\theta$，及びz軸に平行な成分 $B_z$ に分解して考えます。

上図の状況はz軸の周りに回転対称性があるので，$B_\theta$ は円周上のあらゆる点で同じ大きさになっていなければなりません。これより

$$\oint_C \boldsymbol{B} \cdot d\boldsymbol{r} = B_\theta \oint_C dr \\ = 2 \pi r B_\theta$$

また，上図では，電流密度 $\boldsymbol{j}$ は，

$$\boldsymbol{j} = \dfrac{I}{\pi r^2} \boldsymbol{n}$$

一定の大きさの電流を考えているので，磁場及び電場は時間により変化しないと考えてよいです。したがって，

$$\mu_0 \int_S \boldsymbol{j} \cdot \boldsymbol{n} dS + \mu_0 \varepsilon_0 \dfrac{d}{dt} \int_S \boldsymbol{E} \cdot \boldsymbol{n} dS \tag{2} = \mu_0 \dfrac{I}{\pi r^2} \int_S dS + 0 \\ = \mu_0 \dfrac{I}{\pi r^2} \pi r^2 = \mu_0 I$$

(2)式より，これらは等しいので

$$2 \pi r B_\theta = \mu_0 I$$

$$\therefore B_\theta = \dfrac{\mu_0 I}{2 \pi r}$$

$B_\theta$ の方向は電流に対して右ねじの法則にしたがっていることに注意してください。

続いて，$B_r = 0$，$B_z =0$ であることを示しましょう。

系のz軸周りの回転対称性より，もしある円環C上のある一点で $B_r \neq 0$ であるならば，円環C上の全ての点で $B_r$ は同じ大きさでなければなりません。さらに，z軸方向の並行対称性によって，z軸方向に並行移動した円環C’上の全ての点でも，$B_r$ は同じ値でなければなりません。

ここで，下図のような領域を取れば，その表面Sにおいて，(1)式より

$$\int_S \boldsymbol{B} \cdot \boldsymbol{n} =0$$

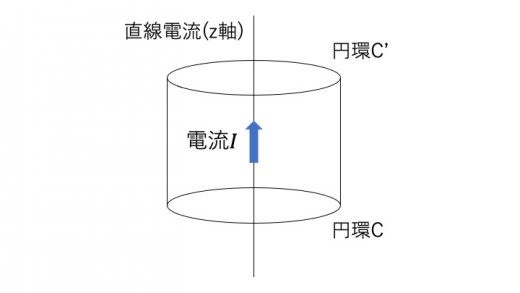
が成り立ちます。ここで，$B_z$ が0でなくとも，並行対称性により底面と上面で磁場は同一の分布を取るため，円筒を貫く磁場の流束は，側面のみになり，

$$2 \pi r B_r =0$$

$$\therefore B_r =0$$

となります。

最後に，$B_z =0$ を示しましょう。 導線周りの回転対称性及びz軸方向の並行対称性より，$B_z$ は電流からの距離 $r$ のみに依る関数となります。

ここで下図のような長方形領域Dを考え，このDに対して(2)式を当てはめます。

$$\oint_C \boldsymbol{B} \cdot d\boldsymbol{r} = \mu_0 \int_D \boldsymbol{j} \cdot \boldsymbol{n} dS \tag{2}$$

Sを通る電流が存在しないことと，$B_r =0$ であることとから，結局

$$B_z(r_a) l - B_z(r_c) l =0$$

$$\therefore B_z(r_a) = B_z(r_c)$$

この式は，空間のあらゆる点で等しい磁場が存在することを要請しています。仮に，直線電流が「十分に長いが無限でない」場合には，無限遠方で $B_z =0$ としてよいことから，空間のあらゆる点で

$$B_z =0$$

と定めることができます(直線電流が無限に長い場合にはさらなる議論が必要になりますが，ここでは割愛します)。

導出した結果をまとめましょう。

ここでは，いくつかの具体例で実際に計算してみることにより，電磁力の性質をより明確に把握しましょう。

並行導線に加わる電流

下図のような2本の並行導線に電流が流れているときを考えます。

まず導線1が受ける力を求めます。上で求めた結果を用いて，導線2を流れる電流 $I_2$ が導線1のある位置に作る磁場 $B_2$ の大きさは

$$B_2 = \dfrac{\mu_0 I_2}{2 \pi r}$$

であり，向きは画面の奥から手前向きである。よって，導線が受ける力 $F_1$ は，

$$F_1 = I_1 B_2 l \sin{\dfrac{\pi}{2}} \\ = \dfrac{\mu_0 I_1 I_2 l}{2 \pi r}$$

$F_1$ の向きはフレミングの左手の法則より水平右向きになります。

次に，導線2が受ける力を求めます。同様にして，導線1を流れる電流 $I_1$ が導線2のある位置に作る磁場 $B_1$ は，，

$$B_1 = \dfrac{\mu_0 I_1}{2 \pi r}$$

であるから，導線2が受ける力 $F_2$ はは

$$F_2 = I_1 B_2 l \sin{\dfrac{\pi}{2}} \\ =\dfrac{\mu_0 I_1 I_2 l}{2 \pi r}$$

$F_2$ の向きは水平左向きとなります。

ここから，$F_1$ と $F_2$ は同じ大きさで互いに引き合う向きとなっていることがわかります。

また，下図のように電流 $I_2$ の流れる向きが逆となっている場合を考えます。

この場合，電流や磁場の大きさは変化しないため，$F_1$ と $F_2$ の大きさは変わらず等しいことがわかります。

一方，$I_2$ の流れる向きが逆になっているため，磁場 $B_2$ の向きは先ほどは逆の画面手前から奥に向かう向きとなります。

このため，フレミングの左手の法則より，$F_1$ の向きも先ほどとは逆で，水平左向きとなります。

同様に考えることで，$F_2$ の向きも先ほどとは逆の水平右向きとなります。

これより，$F_1$ とと $F_2$ は大きさは同じで互いに斥け合う方向にはたらくことがわかります。

この結果をまとめておきましょう。

この定性的な結果が聞かれることもあるので，すぐに求められるようにしておくと良いでしょう。

モーターの内部などに使われているコイルは，この電磁力を巧みに用い，電流が流れている限り延々と回転することができるようになっています。その仕組みを見てみましょう。

コイルが動く仕組みは，電流が受ける電磁力ですが，何もなければ半回転を繰り返すだけで，回り続けることはできません。しかし，図図3のように整流子がつけられていることで，半回転ごとに流れる電流の向きを変えることができます。これにより，コイルは回り続けることができるようになっています。