【解答・解説】北大前期物理2025 第2問 -電磁気-

更新 2025/10/27

2025年度の北大前期物理第2問を解説します。電磁気の単元です。なお，この記事に関する責任は，全て当ウェブサイトに属します。また，解説・解答等は，全て当ウェブサイトが独自に作成したものです。

２つの組A、Bがあり、A組は男子2人、女子3人、B組は男子4人、女子1人から成る。この2つの組みを合わせた合計10人の生 2

この問題の(2)で、模範解答では、|cosθ|<1/2(m=2)、|cosθ|>1/2(m=1)、|cosθ|=1/2( 3

2ーニトロベンズアルデヒドとアセトンのアルドール反応の反応機構を矢印付きの画像で教えてください🙏 4

下記の英文についてお聞きしたいことがございます。彼は僕の半分しか本を持っていない。 He has half as ma 5

問題

以下の問題文および図は，2025年度北海道大学前期日程入試問題物理第2問から引用しています(一部ライターが修正・変更した部分があります)。

第2問

以下の文中の $\fbox{(1)}$ ~ $\fbox{(9)}$ に適切な数式または数値を入れよ。また， $\fbox{(あ)}$ および $\fbox{(い)}$ には各選択肢から最も適切なものを選べ。

問1 図1のように，底面の2辺の長さが $a [\text{m}]$ および $b [\text{m}]$ ，抵抗率が $\rho [\Omega \cdot \text{m}]$ の直方体形状の試料を考える。

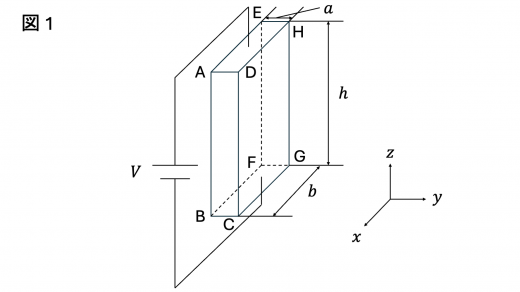
hp25-2-fig1

この試料には数密度が $n [/\text{m}^3]$ で電気量が $-e [\text{C}] (e > 0)$ の自由電子が存在する。また，図1のように座標軸 ( $x$ 軸， $y$ 軸， $z$ 軸) をとり，直方体の各頂点を図1のように A ~ H と名づける。この試料の面 ADHE と面 BCGF の間に起電力が $V [\text{V}]$ の直流電流を接続すると，試料中には $z$ 軸の負の向きに大きさが $\fbox{(1)}$ [V / m] の一様な電場が発生する。このときの自由電子の運動は，静電気力と抵抗力がつりあう運動で，その平均の速さを $v [\text{m}/\text{s}]$ とする。この試料を通って流れる電流の大きさ $I [\text{A}]$ は $v$ を用いて $I = \fbox{(2)} [\text{A}]$ と表されること，および，抵抗力の大きさが $kv [\text{N}]$ のように $v$ に比例することから ( $k$ は比例定数)， $n$ と $\rho$ の間に $\rho = \fbox{(3)} [\Omega \cdot \text{m}]$ の関係があることがわかる。

つぎに， $y$ 軸の正の向きに空間的に一様で磁束密度が $B [\text{T}]$ の磁場をかけた。磁場をかけた瞬間には，自由電子は大きさが $\fbox{(4)} [\text{N}]$ のローレンツ力を受け運動方向が変化するため，図1に示した $\fbox{(あ)}$ とそれに向かいあう面の電圧 $V' [\text{V}]$ を測定することにより，自由電子の数密度 $n$ は $I$ を用いて $n = \fbox{(5)} [/\text{m}^3]$ のように求めることができる。

—

$\fbox{(あ)}$ の選択肢：

(ア) 面 ABCD
(イ) 面 DCGH
(ウ) 面 ABFE
(エ) 面 EFGH
(オ) 面 ADHE
(カ) 面 BCGF

—

問2 図2のように，プラスチック製の円柱にコイル1を巻き，抵抗，直流電流，およびスイッチを用いて直列回路を作成した。

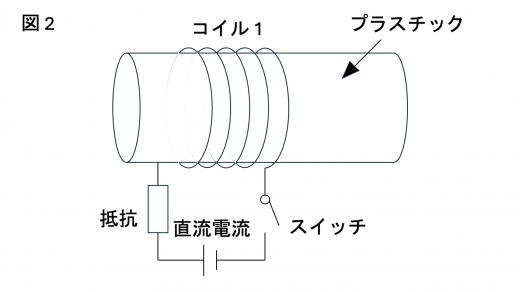
hp25-2-fig2

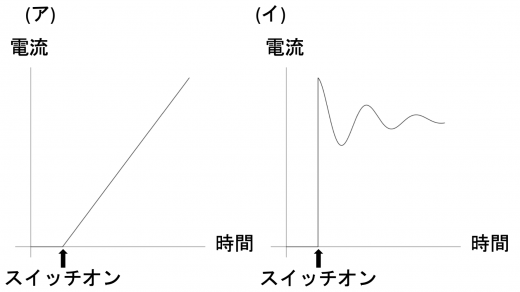
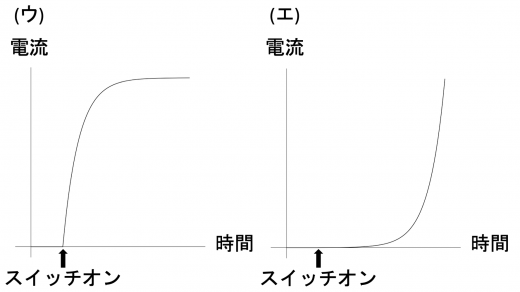
このとき，スイッチを閉じた後で回路が定常状態となるまでのコイル1に流れる電流の時間変化を模式的に描くと $\fbox{(い)}$ のようになる。

—

$\fbox{(い)}$ の選択肢：

hp25-2-2-ans-ai

hp25-2-2-ans-ue

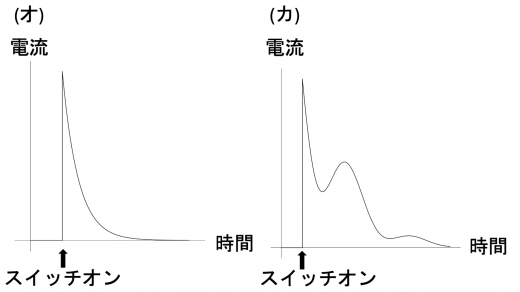
hp25-2-2-ans-oka

—

図3のように，図2のコイル1の隣にコイル2を巻き，コイル2の両端に抵抗値が $10 [\Omega]$ の抵抗を接続した。

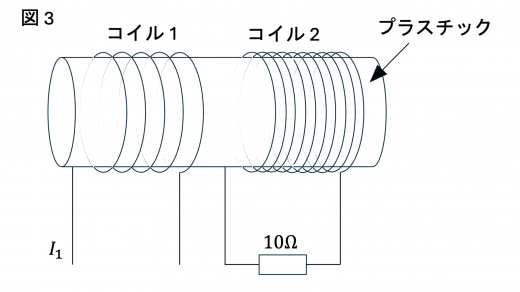
hp25-2-fig3

このとき，コイル1とコイル2の間の相互インダクタンスは $0.05 [\text{H}]$ となった。コイル1に流れる電流 $I_1$ を1秒間に $100 [\text{A}]$ の割合で時間とともに増加させるとき，コイル2に流れる電流は $\fbox{(6)} \text{A}$ となる。

つぎに，図4のように，コイル1とコイル2を巻く円柱を鉄製に変更した。

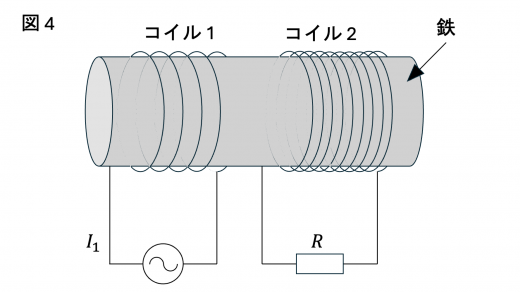
hp25-2-fig4

鉄の透磁率は空気よりはるかに大きいので，コイル1を貫く磁束とコイル2を貫く磁束は等しく，このような装置は変圧器としてはたらく。コイル1の巻き数は $N_1$ 回，コイル2の巻き数は $N_2$ 回であるとする。コイル1に実効値が $V [\text{V}]$ の交流電源を接続し，コイル2の両端に抵抗率が $R [\Omega]$ の抵抗 R を接続したとき，コイル1に流れる電流の実効値は $I_1 = \fbox{(7)} [\text{A}]$ となる。ただし，R を取り除いたとき $I_1 = 0$ となるとする。

最後に，図4と同じ変圧器を2台用意し，図5のように，抵抗値が $r [\Omega]$ の抵抗 r を介して接続した。ただし，変圧器1のコイル2が変圧器2のコイル2に接続されていて，変圧器2のコイル1は抵抗値が不明な抵抗に接続されている。また，変圧器1のコイル1は実効値が $V [\text{V}]$ の交流電源に接続されている。変圧器1と変圧器2の間は十分離れており，一方の磁束は他方に届かないとする。変圧器1のコイル1に流れる電流の実効値を $I [\text{A}]$ とすると，r で発生するジュール熱による損失電力は $P_r = \fbox{(8)} [\text{W}]$ である。それに対し，交流電源から供給される電力は $P = \fbox{(9)} [\text{W}]$ であるため， $N_2$ を $N_1$ より十分おきくすることによって $P_r / P$ を低減できる。

前半はホール効果に関する問題，後半は変圧器に関する問題です。一度は触れておく価値がある問題です。

解答例

問1(1)電場が一様であることより，その大きさ EEE は
E=Vh[V/m]
E = \dfrac{V}{h} [\text{V}/\text{m}]
E=hV​[V/m]
となります (詳しくは 電場・磁場・電荷密度・電流密度｜電磁気学における基本的な物理量，導体内における電場・電位)
。
(2)電子が平均の速さ vvv で，数密度 nnn，底面積 S=abS = abS=ab の方向に
試料内を運動することから，電流の大きさの公式より
I=vabne[A]
I = vabne [\text{A}]
I=vabne[A]
と求められます。
(3)
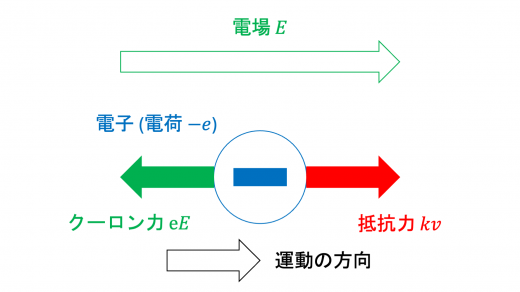
定常状態では，試料内で電子は等速運動を行っています。したがって，試料内の電子にはたらく抵抗力とクーロン力がつりあっています。
問題文と合わせて，力のつりあいより
kv=eE
kv = eE
kv=eE
という関係が成り立ちます。
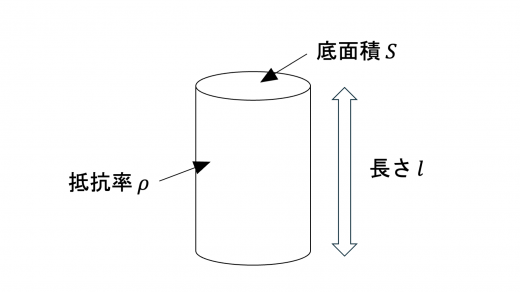
また，抵抗値 RRR の抵抗が上図のような構造をしているとき，抵抗値 RRR と抵抗率 ρ\rhoρ との間には
R=ρlS
R = \rho \dfrac{l}{S}
R=ρSl​
という関係が成り立つことに注意します。いまの試料の場合，l=h,S=abl = h, S = abl=h,S=ab となっています。
ρ\rhoρ を nnn で表すために，まず RRR を既知の量で表してみましょう。そのためには，オームの法則 (オームの法則と抵抗の性質) より V=RIV = RIV=RI が成り立つことを利用します。
力のつりあいの式より
E=kve
E = \dfrac{kv}{e}
E=ekv​
(1) の結果より
Vh=kve
\dfrac{V}{h} = \dfrac{kv}{e}
hV​=ekv​
V=hkve=hkeIabne=ke2nhSI
\begin{aligned}
V &= h \dfrac{kv}{e} \\
&= h \dfrac{k}{e} \dfrac{I}{abne} \\
&= \dfrac{k}{e^2 n} \dfrac{h}{S} I
\end{aligned}
V​=hekv​=hek​abneI​=e2nk​Sh​I​
オームの法則より，この比例定数が RRR となるので
R=ke2nhS
R = \dfrac{k}{e^2 n} \dfrac{h}{S}
R=e2nk​Sh​
RRR と ρ\rhoρ との関係より，ρ\rhoρ と nnn との関係として
ρ=ke2n[Ω⋅m]
\rho = \dfrac{k}{e^2 n} [\Omega \cdot \text{m}]
ρ=e2nk​[Ω⋅m]
が成り立つことがわかります。
(注) この関係は，オームの法則の議論をするときに自然と登場する関係式にもなっています。詳しくは オームの法則と抵抗の性質 をご覧ください。
次元の検算実際に上式の右辺の単位が Ω⋅m\Omega \cdot \text{m}Ω⋅m となっていることを確かめましょう。以下では物理量 AAA の次元を <A><A><A> で表します。
まず，kkk の次元について確認します。<kv>=N=kg⋅m/s2<kv> = \text{N} = \text{kg} \cdot \text{m} / \text{s}^2<kv>=N=kg⋅m/s2 より
<k>=kg/s
<k> = \text{kg}  / \text{s}
<k>=kg/s
また <e>=C=s⋅A<e> = C = \text{s} \cdot \text{A}<e>=C=s⋅A より
<ρ>=kg/ss2⋅A2/m3=kg⋅m3/(s3⋅A2)
\begin{aligned}
<\rho> &= \dfrac{\text{kg} / \text{s}}{\text{s}^2 \cdot \text{A}^2 / \text{m}^3} \\
&= \text{kg} \cdot \text{m}^3 / (\text{s}^3 \cdot \text{A}^2)
\end{aligned}
<ρ>​=s2⋅A2/m3kg/s​=kg⋅m3/(s3⋅A2)​
次に Ω\OmegaΩ を SI 単位系で表します。オームの法則と，<eV>=J=kg⋅m2/s2<eV> = \text{J} = \text{kg} \cdot \text{m}^2 / \text{s}^2<eV>=J=kg⋅m2/s2 より，
<R>=Ω=<VI>=kg⋅m2/(s3⋅A)A=kg⋅m2/(s3⋅A2)
\begin{aligned}
<R> &= \Omega = \left< \dfrac{V}{I} \right> \\
&= \dfrac{\text{kg} \cdot \text{m}^2 / (\text{s}^3 \cdot \text{A})}{\text{A}} \\
&= \text{kg} \cdot \text{m}^2 / (\text{s}^3 \cdot \text{A}^2)
\end{aligned}
<R>​=Ω=⟨IV​⟩=Akg⋅m2/(s3⋅A)​=kg⋅m2/(s3⋅A2)​
したがって，ρ\rhoρ の次元は
<ρ>=Ω⋅m
<\rho> = \Omega \cdot \text{m}
<ρ>=Ω⋅m
となっており，確かめられました。
(4)ローレンツ力の大きさの公式 (ローレンツ力の意味と式｜磁場中の荷電粒子の運動) より，電子にはたらくローレンツ力の大きさ fff は
f=∣−e∣vB=evB[N]
\begin{aligned}
f &= |-e| v B = evB [\text{N}]
\end{aligned}
f​=∣−e∣vB=evB[N]​
と求められます。
(あ)
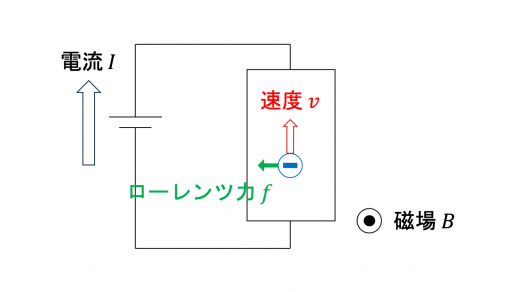
上図のように電流，電子の運動，および磁場の方向が定まっているとき，電子に働くローレンツ力は上図の xxx 軸正の方向にはたらきます。
したがって，定常状態では，電子は面 ABCD に局在することになります。
したがって，負に帯電するのは (ア)：面 ABCD です。
(5)試料の xxx 軸正方向には電場 E′=V′/bE' = V' / bE′=V′/b がはたらいています。
定常状態で試料にはたらく力のつりあいより
eE′=evB
e E' = e v B
eE′=evB
E′=V′/bE' = V' / bE′=V′/b および v=I/abnev = I / abnev=I/abne を代入して
eV′b=eIabneB
e \dfrac{V'}{b} = e \dfrac{I}{abne} B
ebV′​=eabneI​B
∴n=BIV′ae
\therefore n = \dfrac{BI}{V' a e}
∴n=V′aeBI​
問2(い)定性的な考察から求めるグラフを導きます。まず，十分時間が経った時の電流について考えます。
このとき，電流は時間変化がない定数になっていると考えられます。
したがって，コイルには自己誘導起電力 (自己誘導と自己インダクタンス｜回路に生じる逆起電力の導出)が生じないと考えられます。
このとき回路に流れている電流は，キルヒホッフの第2法則より V/R(>0)V / R (>0)V/R(>0) になっています。これより，電流の時間変化を表すグラフは
(イ) または (ウ) であると考えられます。
また，この設問で用いる電源は直流電源であり，定常状態に至るまで電流の流れる向きは変わりません。したがって，(イ) のような電流の時間変化は生じないことになります。よって，求めるグラフは (ウ) と求まります。
(別解) 微分方程式を解くことにより，電流と時間との関係を直接
導くことも可能です (微分方程式の解法(同次形・線形微分方程式))。
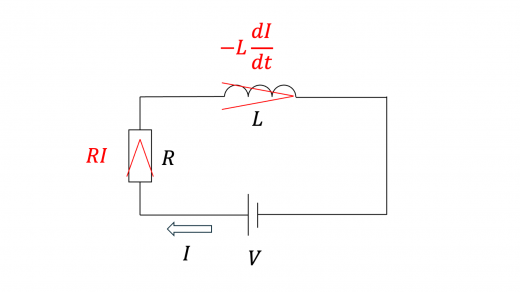
上図の回路で，キルヒホッフ第2法則 (キルヒホッフの法則の解説と例題) より，
V−RI−LI˙=0
V - RI - L \dot{I} = 0
V−RI−LI˙=0
∴LI˙=V−RI=−R(I−VR)
\therefore L \dot{I} = V - RI = - R \left( I - \dfrac{V}{R} \right)
∴LI˙=V−RI=−R(I−RV​)
∴I˙=−RL(I−VR)
\therefore \dot{I} = - \dfrac{R}{L} \left( I - \dfrac{V}{R} \right)
∴I˙=−LR​(I−RV​)
i=I−VRi = I - \dfrac{V}{R}i=I−RV​ とおくと，i˙=I˙\dot{i} = \dot{I}i˙=I˙ であり，上の微分方程式は
i˙=−RLi
\dot{i} = - \dfrac{R}{L} i
i˙=−LR​i
これは，関数を時間微分すると元の関数の定数倍になるという関係を表しています。このような関係を満たす関数は，指数関数 eate^{at}eat です。
この指数関数を時間微分すると，ttt の係数 aaa が係数として落ちてきます。
今回の設問に当てはめると，
i=Ae−RLt
i = A e^{- \frac{R}{L} t}
i=Ae−LR​t
∴I=Ae−RLt+VR
\therefore I = A e^{- \frac{R}{L} t} + \dfrac{V}{R}
∴I=Ae−LR​t+RV​
ここに，AAA は初期条件により定まる定数です。
電流は急激に有限の値は取らず連続的に変化するので，t=0t = 0t=0 のとき I=0I = 0I=0 となります。これより AAA を求めると
0=A+VR
0 = A + \dfrac{V}{R}
0=A+RV​
∴A=−VR
\therefore A = - \dfrac{V}{R}
∴A=−RV​
したがって，電流の時間変化を表す式は
I=VR(1−e−RLt)
I = \dfrac{V}{R} (1 - e^{- \frac{R}{L} t})
I=RV​(1−e−LR​t)
この ttt と III の関係を表すグラフは，(ウ) となります。
(6)コイル 1 とコイル 2 が図 3 のように接続されているとき，コイル 1 に流れている電流 I1I_1I1​ の時間変化によって，コイル 2 には相互誘導起電力がはたらきます。そのときの起電力の大きさ VindV_{ind}Vind​ は，コイル 1 とコイル 2 の相互インダクタンスを MMM とすると
Vind=M∣ΔI1Δt∣
V_{ind} = M \left| \dfrac{\Delta I_1}{\Delta t} \right|
Vind​=M∣∣​ΔtΔI1​​∣∣​
いま，問題文より M=0.05[H],∣ΔI1Δt∣=100[A/s]M = 0.05 [\text{H}], \left| \dfrac{\Delta I_1}{\Delta t} \right| = 100 [\text{A}/\text{s}]M=0.05[H],∣∣​ΔtΔI1​​∣∣​=100[A/s] であるから，
Vind=0.05×100=50[V]
V_{ind} = 0.05 \times 100 = 50 [\text{V}]
Vind​=0.05×100=50[V]
したがって，コイル 2 に流れる電流 I2I_2I2​ は，オームの法則より
I2=VindR=5010=5[A]
I_2 = \dfrac{V_{ind}}{R} = \dfrac{50}{10} = 5 [\text{A}]
I2​=RVind​​=1050​=5[A]
と求められます。
(7)コイルの巻き数と生じる電圧との間には
V2V=N2N1(7-1)
\dfrac{V_2}{V} = \dfrac{N_2}{N_1} \tag{7-1}
VV2​​=N1​N2​​(7-1)
という関係があります (詳しくは 相互誘導と相互インダクタンスの定義｜変圧器の回路の例題)。
また，理想的な変圧器では，エネルギー保存則が保たれ，コイル 1による電力とコイル 2 による電力が等しくなります。したがって
I1V=I2V2(7-2)
I_1 V = I_2 V_2 \tag{7-2}
I1​V=I2​V2​(7-2)
さらに，コイル 2 を含む回路において，キルヒホッフ第2法則より
V2=I2R(7-3)
V_2 = I_2 R \tag{7-3}
V2​=I2​R(7-3)
未知数は V2,I1,I2V_2, I_1, I_2V2​,I1​,I2​ であり，数式は 3 つなので，これらより全ての未知数が求められます。
(7-1) 式より，V2/VV_2 / VV2​/V は定数の比によって表されることを利用することを考えます。
(7-3) 式を用いて (7-2) 式の I2I_2I2​ を消去して
I1V=V22R
I_1 V = \dfrac{V_2^2}{R}
I1​V=RV22​​
(7-1) 式を利用して変数を消去することを見越して式変形すると
I1=V22VR=(V2V)2VR=(N2N1)2VR
\begin{aligned}
I_1 &= \dfrac{V_2^2}{V R} \\
&= \left( \dfrac{V_2}{V} \right)^2 \dfrac{V}{R} \\
&= \left( \dfrac{N_2}{N_1} \right)^2 \dfrac{V}{R}
\end{aligned}
I1​​=VRV22​​=(VV2​​)2RV​=(N1​N2​​)2RV​​
と求められます。
(8)
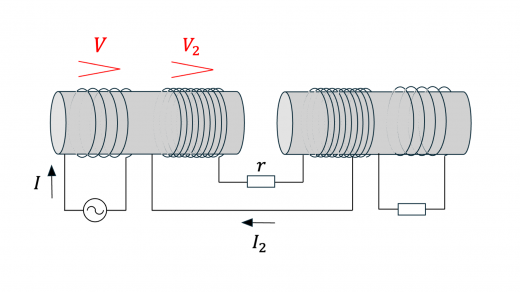
上図のように，各変圧器のコイルにはたらく電圧および流れる電流を V,V2,I,I2V, V_2, I, I_2V,V2​,I,I2​ とし，これらの関係を求めていきます。
変圧器 1 における電圧と巻き数の関係より
V2V=N2N1(8-1)
\dfrac{V_2}{V} = \dfrac{N_2}{N_1} \tag{8-1}
VV2​​=N1​N2​​(8-1)
変圧器 1 における理想的な変圧器の条件より
VI=V2I2(8-2)
V I = V_2 I_2 \tag{8-2}
VI=V2​I2​(8-2)
抵抗値 rrr の抵抗 r で生じるジュール熱 PrP_\text{r}Pr​ は
Pr=r(I2)2
P_\text{r} = r (I_2)^2
Pr​=r(I2​)2
と求められるので，I2I_2I2​ を求めましょう。(8-1)・(8-2) 式より
I2=VV2I=N1N2I
\begin{aligned}
I_2 &= \dfrac{V}{V_2} I \\
&= \dfrac{N_1}{N_2} I
\end{aligned}
I2​​=V2​V​I=N2​N1​​I​
これを代入して，PrP_\text{r}Pr​ は
Pr=(N1N2)2rI2
P_\text{r} = \left( \dfrac{N_1}{N_2} \right)^2 r I^2
Pr​=(N2​N1​​)2rI2
となります。
(9)交流電源から供給される電力は，その電源の電圧および電流の実効値から
求められ
P=VI
P = VI
P=VI
と表されます。
これより，N2N_2N2​ を小さくすることで，PrP_\text{r}Pr​ ひいては Pr/PP_\text{r} / PPr​/P を低減することができます。
ホール効果に関して，量子力学の効果を考慮することで起こる，量子ホール効果という現象が知られています。興味のある方はぜひ調べてみてください。