ローレンツ力の意味と式|磁場中の荷電粒子の運動
ローレンツ力は,高校物理で非常に頻出なテーマの一つです。その理由として,以下の2つが挙げられると思います。1つ目は,力の向きと大きさとを正確に理解する必要があること。2つ目は,電磁気と力学との融合問題になることです。
ローレンツ力とは何かしっかり理解し,議論に慣れておきましょう。
この記事に関連するQ&A
ローレンツ力とその公式
ローレンツ力とその公式
ローレンツ力とは
ローレンツ力とは,電荷を帯びた粒子が磁場内を運動するときに,その磁場から受ける力のことです。
いま,一様な磁場 [T] の中を,大きさ [C] の電荷を持った荷電粒子が速さ [m/s] で運動しているとします。粒子の速度 と磁場ベクトル とのなす角が であるとき,粒子が磁場から受けるローレンツ力 [N]は以下の公式で表すことができます。
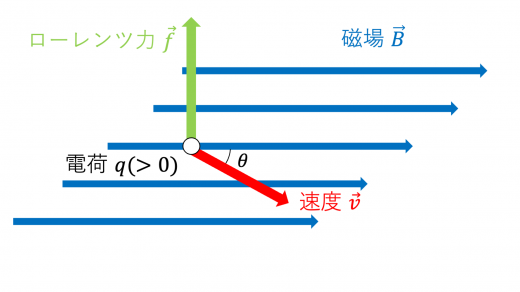
ローレンツ力の単位が [N] になることは,次元解析により確かめられます。
であるから,
高校物理の範囲では,この公式の導出は与えられないため,覚えるしかない公式になっています。問題を多く解いて,染み込ませておきましょう。
ローレンツ力の向きは,荷電粒子の速度と磁場に応じて決まります。これは,以下に述べるように,フレミングの左手の法則あるいは右ねじの法則によって定まります。
ローレンツ力の向き
ローレンツ力の向きは以下に述べる2つの方法から決めることができます。どちらか1つを確実に使えるようになりましょう。
フレミングの左手の法則から決める
フレミングの左手の法則については フレミングの左手の法則の復習・理論的解説|電磁力の定義|中学から高校まで をご覧ください。
電荷が正の時のローレンツ力の向きは,電荷の速度を中指,磁場の向きを人差し指としたときの親指の向きとなります。
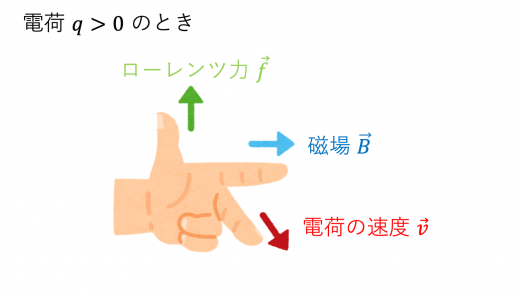
電荷が負の時のローレンツ力の向きは,速度の逆の向きを中指,磁場の向きを人差し指としたときの親指の向きとなります。
手の画像についてはいらすとや様よりお借りしました。
右ねじの方向から決める
右ねじの法則については 電流と磁束密度の関係 をご覧ください。
電荷が正のときのローレンツ力の向きは,速度 を磁場 に重ねるように回すとき,ねじが進む方向にはたらきます。
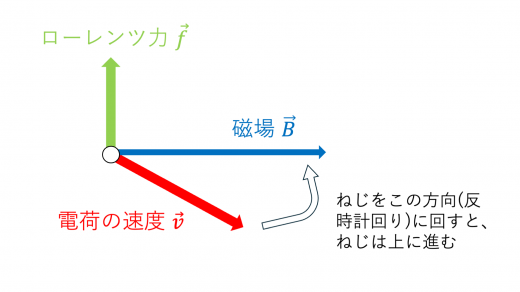
電荷が負の時は,速度と逆方向のベクトルに対して同じことをしてやればよいです。
右ねじの法則を用いる場合は,「電荷の速度を磁場に合わせるように回す」ことに注意してください。
【応用】外積を用いたローレンツ力の表現
ローレンツ力の公式は,外積を用いても表現することができます。外積は高校数学の範囲ではないので,興味のある方のみご覧ください。
外積については,ベクトルの内積と外積の意味と嬉しさ をご覧ください。
いま,電荷 を帯びた粒子が,一様な磁場 内を速度 で運動しているとき,この粒子が磁場から受ける力 は
と表現できます。
まず,このベクトル の大きさ を求めましょう。ベクトル の大きさは,外積の定義より, と とのなす角度を として, と求められます。したがって,ローレンツ力の大きさは
と求められます。
次に, の向きを考えます。これは,外積の定義より, と の両方に垂直な方向になります。この方向はまさに,フレミングの左手の法則(あるいは右ねじの法則)から定める方向と同一のものになっています。
ローレンツ力と電磁力との関係
ローレンツ力と電磁力との関係
電流が磁場から受ける力として,電磁力があります。電磁力については,フレミングの左手の法則の復習・理論的解説|電磁力の定義|中学から高校まで をご覧ください。
ローレンツ力と電磁力は,本質的には同一のものであることを示すことができます。
ローレンツ力から,電流が磁場から受ける電磁力が得られることを確かめる。
下図のように,一様な磁場 内に置かれた長さ の動線内を,一様な電流 が流れているときを考える。簡単のため,磁場 は 軸正の方向を向いていると考える。
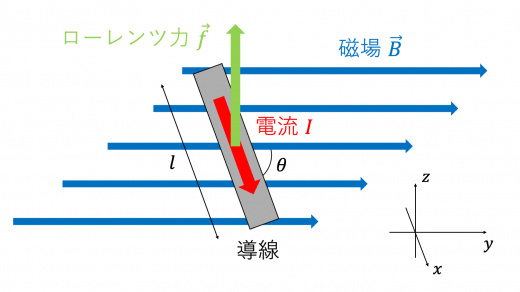
このとき,電流が磁場から受ける電磁力の大きさ は
と表される。電磁力の向きは, 軸正の方向となっている。
一方,電流は,電荷 の複数の電子が,速さ で運動していると考えることもできる。
この電荷1個が受けるローレンツ力 は
と表すことができる。また,電子の動きは電流の向きと逆であり,かつ電子の電荷は負であることを考えると,このローレンツ力の向きは 軸の正の方向となる。
いま,電流が流れている導線の底面積を ,電子の数密度を とすると,
という関係がある(詳しくは別記事にて解説予定です)。これより,この導線の長さ の範囲には,電子が
個存在すると考えられる。ローレンツ力は同じ 軸正の方向を向いているので,その合力の大きさは,各ローレンツ力の大きさを足し合わせることで求められ,
また,合力の向きは 軸正の方向となる。
よって,電荷が受けるローレンツ力と電流が受ける電磁力とは,本質的には同一のものである。
例題
例題
一様な磁場中の荷電粒子の運動を考察する問題を考えてみましょう。非常に典型的な問題の1つとなっています。
以下のような 空間の原点に,質量 ,電荷 を持った粒子が置かれている。このとき,空間全体には一様に磁場 がはたらいているとする。また,重力は無視する。
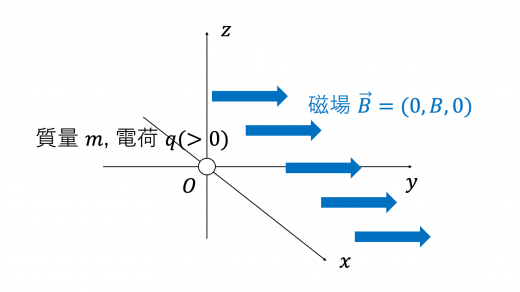
まず,荷電粒子を 軸正の方向に,速さ で打ち出すことを考える。
(1)このとき,荷電粒子が円運動することを説明せよ。
(2)この円運動の半径 と,荷電粒子の軌跡が描く円の中心 の座標 を求めよ。
次に,荷電粒子を 軸正の方向に,速さ で打ち出すことを考える。
(3)このときの荷電粒子の運動はどのようになるか説明せよ。
最後に,荷電粒子を 平面上で, 軸正の方向となす角が となるように,速さ で打ち出すことを考える。
(4)このときの荷電粒子の運動はどのようになるか説明せよ。
(5)粒子の運動の軌跡が原点の次に 軸と交わる点をQとする。点Qの座標を求めよ。もし原点を離れた後一度も 軸と交わらない場合は,「存在しない」と答えよ。
(1)ローレンツ力は,その定義より,荷電粒子の運動の方向と常に垂直に働くため,荷電粒子に対して仕事をしない。いま,磁場の大きさが一様であることから,荷電粒子は,自らの運動の方向とは垂直な方向に一定な力を受けながら,同じ速さで運動をし続ける。これより,荷電粒子の運動は円運動となる。
(2)この円運動の半径を求める。円運動の加速度は,速さ を用いて と書くことができる。円運動の運動方程式より
と求められる。
この荷電粒子ははじめ原点 にあり, 軸正方向に打ち出された。ローレンツ力ははじめ 軸負方向にはたらくため,荷電粒子は 面の の領域を,原点 を通り,半径 で円運動する。この円の軌跡は下図のようになる。
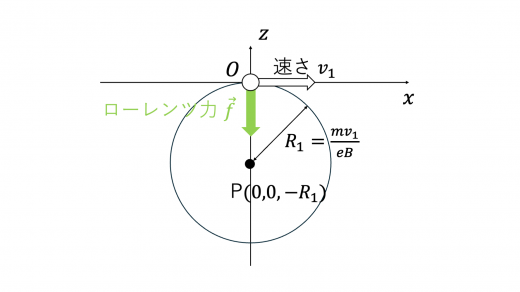
したがって,この円の中心 の座標は
と求められる。
(3)はじめ,運動の方向と磁場の方向とが平行になっているため,粒子にはたらくローレンツ力は0となる。したがって,はじめ粒子は 軸正の方向に速さ で等速直線運動する。その後も粒子の運動の方向と磁場の方向とが平行になっているため,粒子にはたらくローレンツ力は0のままであり,粒子の速度は不変のまま保たれる。したがって,荷電粒子の運動は, 軸正の方向に速さ で進む等速直線運動となる。
(4)荷電粒子は 軸方向に速度成分 , 軸方向に速度成分 を持つ。したがって,荷電粒子は 平面上で速さ の円運動をしながら, 軸正の方向に速さ で等速直線運動する。 空間では,この運動は螺旋運動となる。
(5)粒子が原点を離れたあと,再び 軸上に粒子が到達するのは, 平面での円運動が1周したときである。粒子が原点を離れて1周が終わるまでの時間を とすると, は 平面での円運動の周期に相当する。
まず,この円運動の半径 を求める。(2)での議論より
したがって
粒子は 軸正方向に等速直線運動しているので,点Qの 座標を とすると
したがって,点Qの座標は である。
円運動について,詳しくは 円運動とは|円運動における加速度・向心力・遠心力 を参照してください。
ローレンツ力は,定義をしっかり覚えることが重要になります。この記事でもいくつか公式を紹介しましたが,そのうち1つで良いので確実に使えるようになりましょう。











