相互誘導と相互インダクタンスの定義｜変圧器の回路の例題

更新 2021/12/22

この記事は，相互誘導について解説します。まず，相互誘導の定義について述べた後，相互インピーダンスの具体的な表式を与えます。また，相互誘導の代表例題である，変圧器の問題を紹介し，結合係数やインピーダンスの概念を解説します。

相互誘導の定義

相互誘導と関連の深い概念として，自己誘導があります。自己誘導については，以下の記事を参照してください。

自己誘導と自己インダクタンス｜回路に生じる逆起電力の導出

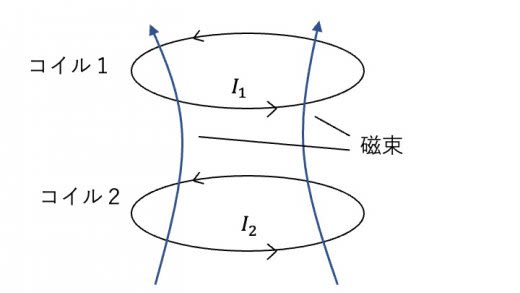まず，相互誘導とは何かを理解するために，上で紹介した自己誘導の記事と同様の例を見ていきましょう。上の図では，2つのコイルがあり，コイルには電流が流れています。よく知られているように，空間に電流があると，磁場が生じます。では，上のような2つのコイルの作る磁場は，どのように表せるでしょうか。
磁場の生じる原因は，コイル1,2に流れる電流 I1,I2I_1,I_2I1​,I2​ なので，磁束は I1,I2I_1,I_2I1​,I2​ の関数になると考えられます。
このように，コイルを貫く磁束が，異なるコイルを流れる電流によって生成されることを相互誘導と言います。

この漢字の読みを教えてください 2

有理化をしないでtに置き換えて計算すると答えが違くなってしまうんですが何故ですか？どこか間違ってますか？ 3

シリンジに栓をして引っ張り、栓を外した時の吸引力はそのシリンジの体積で強くなりますか？それを示す数式などはありますか？ 4

数三でロピタルの定理なみに使う定理を教えてください 5

相互インダクタンスの定義

実は，コイルを貫く磁束の関数を，Maxwell方程式を解いて具体的に求めてみると、I1,I2I_1,I_2I1​,I2​ の線型結合になることがわかっています。(Maxwell方程式を解くのには，大学レベルの高度な知識が必要なので，省略します。)
すなわち，コイル1,2を貫く磁束をそれぞれ ϕ1,ϕ2\phi_1,\phi_2ϕ1​,ϕ2​ とすると，
ϕ1=L11I1+L12I2ϕ2=L21I1+L22I2
\begin{aligned}
\phi_1&=L_{11}I_1+L_{12}I_2\\
\phi_2&=L_{21}I_1+L_{22}I_2
\end{aligned}
ϕ1​ϕ2​​=L11​I1​+L12​I2​=L21​I1​+L22​I2​​
の関係が成り立ちます。
I1,I2I_1,I_2I1​,I2​ の係数として，Lij(i,j=1,2)L_{ij} (i,j=1,2)Lij​(i,j=1,2) を用いています。ここで i=ji=ji=j の時の係数，すなわち　L11L_{11}L11​ と　L22L_{22}L22​ は自己インダクタンスと呼ばれています。自己インダクタンスについても、前述の記事を参照してください。
i≠ji\neq ji=j の時の係数，すなわち　L12L_{12}L12​ と　L21L_{21}L21​ は相互インダクタンスと呼ばれています。相互インダクタンスとは，異なるコイル同士の電流がお互いのコイルを貫く磁束を作る際の係数です。
自己インダクタンスと相互インダクタンスの単位は
[H]=[W/A]=[V⋅s⋅A−1]=[m2⋅kg⋅s−2⋅A−2]
\begin{aligned}
\mathrm{[H]}&=\mathrm{[W/A]}\\
&=\mathrm{[V\cdot s\cdot A^{-1}]}\\
&=\mathrm{[m^2\cdot kg\cdot s^{-2}\cdot A^{-2}]}
\end{aligned}
[H]​=[W/A]=[V⋅s⋅A−1]=[m2⋅kg⋅s−2⋅A−2]​
で与えられます。ここで，H\mathrm{H}H はヘンリーと読みます。
相互誘導は，上で紹介したようなコイルが，2つのみの場合だけでなく，コイルが多数ある場合にも拡張することができます。この時，kkk 番目のコイルを貫く磁束 ϕk\phi_kϕk​ は，以下の式で与えられます。
ϕk=∑jLkjIi
\phi_k=\sum_{j}L_{kj}I_i
ϕk​=j∑​Lkj​Ii​

(発展)Neumannの公式と相反定理

実は，自己インダクタンスや相互インダクタンスの表式は以下で与えられることがわかっています。

Neumannの公式

$L_{ij}=\dfrac{\mu}{4\pi}\oint_{C_i}\oint_{C_j }\dfrac{d\boldsymbol{x_i}\cdot d\boldsymbol{x_j}}{|d\boldsymbol{x_i}-d\boldsymbol{x_j}|}$

ここで $C_i,C_j$ は上の図のコイル1,2に対応しており， $\boldsymbol{x_i},\boldsymbol{x_j}$ は2つのコイルの接線方向の単位ベクトルです。導出には，大学3年生レベルの数学と電磁気学の理解が必要です。

この式を見ると明らかなように，相互インダクタンスにおいて以下の重要な定理が成り立ちます。

相反定理

インダクタンスについて，以下の等式が成り立つ。 $L_{ij}=L_{ji}$

例えば， $\begin{aligned} \phi_1&=L_{11}I_1+L_{12}I_2\\ \phi_2&=L_{21}I_1+L_{22}I_2 \end{aligned}$ において， $L_{12}=L_{21}$ が成り立ちます。

大学入試などの問題では，相反定理を暗黙の了解として認め， $L_{ij}=M \quad(i\neq j)$ のように $M$ を使うことが多いです。

相互誘導の例題

相互誘導現象の例題として，以下の回路を計算してみましょう。以下の環状鉄心の装置は，変圧器などに応用されています。

例題

以下の図に示すように，環状鉄心の左側に，巻き数 $n_1$ ，右側に巻き数 $n_2$ のコイルが巻いてある。これらのコイルに電流を流した時，鉄針内にのみ磁束 $\phi$ が生じる。

(1)磁束 $\phi$ は，回路に流れる電流 $I_1,I_2$ を用いて， $\phi=k(n_1I_1+n_2I_2)$ と表されることを示せ。ただしここで $k$ は適当な定数である。

(2)与えられた系について，回路方程式を立てよ。

(3)回路に生じる誘導起電力の比， $\dfrac{V_2}{V_1}$ を求めよ。変圧器　一次コイルと二次コイル

解答

(1) 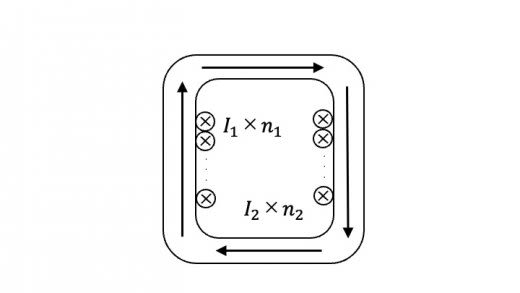上の環状鉄針のループにAmpereの法則を適応する。透磁率を $\mu_0$ ，磁束密度を $B$ ，ループの週の長さを $l$ とすると， $\dfrac{Bl}{\mu_0}=n_1I_1+n_2I_2$ を得る。

よって $\phi$ は， $\phi=k(n_1I_1+n_2I_2)$ の形になる。

(2)まず，左側の回路のループにキルヒホッフの法則を用いると， $E=R_1I_1+V_1$ となる。また，Faradayの法則より， $V_1=n_1\dfrac{d\phi}{dt}$ を得る。

右側の回路でも，同様に考えることで， $\begin{aligned} 0&=R_2I_2+V_2\\ V_2&=n_2\dfrac{d\phi}{dt} \end{aligned}$ を得る。以上をまとめると， $\begin{aligned} E&=R_1I_1+V_1\\ V_1&=n_1\dfrac{d\phi}{dt}\\ 0&=R_2I_2+V_2\\ V_2&=n_2\dfrac{d\phi}{dt} \end{aligned}$ となる。

(3)(2)で得られた式を用いると， $\dfrac{V_2}{V_1}=\dfrac{n_2\dfrac{d\phi}{dt}}{n_1\dfrac{d\phi}{dt}}=\dfrac{n_2}{n_1}$ を得る。

Ampereの法則やFaradayの法則については，以下の記事を参照してください。
マクスウェル方程式

結合係数とインピーダンス

上の例題で左側に巻いてあるコイルを，一次コイル，右側に巻いてあるコイルを，二次コイルと呼びます。また，(3)の結果で，起電力の比と，巻き数の比が等しくなるという結果を得ました。これは，磁束が環状鉄心から漏れ出ないという条件を考慮した結果です。一般に漏れ出る場合は，適当な比例定数 $k$ を用いて $\dfrac{V_2}{V_1}=k\dfrac{n_2}{n_1}$ と表します。ここで $k$ を結合係数と呼びます。

また，変圧器を評価するための指標として，インピーダンス $Z=\dfrac{E}{I}$ も，しばしば用いられます。

結合定数やインピーダンスは定義量なので，求め方は上に与えた式によります。

上の解答からもわかるように，相互誘導によって磁場が生じ，その結果Faradayの法則により，誘導起電力が生じます。この誘導起電力が生じることを，相互誘導と呼ぶこともあります。

変圧器の問題は，難関大学でしばしば出題されます。