点電荷の重要性質｜クーロン力とポテンシャル

更新 2022/02/09

この記事では点電荷の性質について解説します。点電荷の重要な性質として，「点電荷のつくる磁場」，「点電荷のポテンシャル」などがあります。これらを完璧に抑えることが，まず電磁気学を学ぶ上で大切なことになります。

点電荷とは

点電荷とは，簡単にいうと電荷 $q$ を持った質点です。ここでの電荷の大きさ $q$ は，電気素量 $e\simeq 1.602\times 10^{-19}\mathrm{C}$ の整数倍であることが知られています。
基本的には，以下の記事で紹介されているような一般的な性質に従います。
電荷と電気量保存の法則

点電荷は電磁気学において最も基本的な対象なので，あいまいさなくしっかりと性質を抑えておく必要があります。

(発展)点電荷の数学的な表示

点電荷の作る電場も電磁気学の基本方程式である，Maxwell方程式にしたがいます。それを計算するには，「点電荷とはなんなのか」ということを数学的に表す必要があります。点電荷とはすなわち，「ある一点で電荷が $q$ であり，その他の場所では0という電荷分布を与えるもの」ということになります。

このようなことを考えると，位置 $\boldsymbol r$ にある点電荷 $q(\boldsymbol r)$ の電荷分布 $\rho(\boldsymbol r)$ は以下で与えられます。

点電荷の電荷分布

$\rho(\boldsymbol r)=q\delta^3(\boldsymbol r-\boldsymbol r')$

ここで $\delta^3(\boldsymbol r-\boldsymbol r')$ という見慣れない記号が出てきましたが，これは

ディラックのデルタ関数（一次元）

実数 $x$ に対して， $\begin{cases} \delta (x) = \begin{cases} 0 & (x \neq 0)\\ \infty & (x = 0) \end{cases}\\ \displaystyle \int_{-\infty}^{\infty} \delta(x) dx = 1 \end{cases}$ という性質をもつ関数 $\delta (x)$ をデルタ関数という。

を3次元に拡張したものです。(なので形式的に3乗の記号を書いています。)

デルタ関数についてもっと知りたい方は，以下の記事をご覧ください。
ディラックのデルタ関数
 デルタ関数でポアソン方程式の特殊解・境界条件下の解の一意性を導出

公民の時事問題対策に最近のニュースを教えてください。政治や裁判など、公民に関連するニュースでお願いします。できるだけ簡潔 2

塩は、陽イオン陰イオンの順に書くと国際的に決まっていると習ったのですが、なぜこれは陰イオンが先に書かれてあるのですか？調 3

読書感想文(もしくはエッセイ)です。青空文庫にある梶井基次郎の「檸檬」のあらすじと、おすすめしたいポイントを教えてく 4

古文の宿題です。「項梁教籍兵法。」の現代語訳について教えてください。エピソードと経緯、時代背景も一緒にお願いします。 5

点電荷のつくる電場・クーロン力

以下では点電荷のつくる電場の公式を導出していきます。導出には，Maxwell方程式の一つである，Gaussの法則を用います。
Gaussの法則(積分形)
∫SE⋅ndS=1ε0∫VρdV
\int_S\boldsymbol E\cdot \boldsymbol n dS=\dfrac{1}{\varepsilon_0}\int_V \rho dV
∫S​E⋅ndS=ε0​1​∫V​ρdV
ここで ε0\varepsilon_0ε0​ は真空の誘電率です。
Gaussの法則の意味を簡単に解説します。
右辺は，ある空間を適当な閉曲面で囲んだとき，その中にある全電荷の大きさの総和を取ることを表します。
左辺は，その閉曲面の表面を貫く全電場を表します。
この2つが等しくなる，というのがGaussの法則です。

以上を踏まえて，点電荷にGaussの法則を適用してみます。

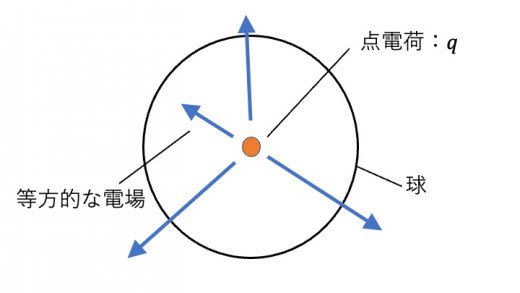閉曲面として，点電荷を中心とする，半径 rrr の球をとってみます。すると，Gaussの法則の右辺は，閉曲面の中には電荷 qqq のみがあることから，
1ε0∫VρdV=qε0
\dfrac{1}{\varepsilon_0}\int_V \rho dV=\dfrac{q}{\varepsilon_0}
ε0​1​∫V​ρdV=ε0​q​
となります。
左辺は，電場は球を一様等方に貫いていることから，
∫SE⋅ndS=E⋅4πr2
\int_S\boldsymbol E\cdot \boldsymbol n dS=E\cdot4\pi r^2
∫S​E⋅ndS=E⋅4πr2
となります。
E⋅4πr2=qε0
E\cdot4\pi r^2=\dfrac{q}{\varepsilon_0}
E⋅4πr2=ε0​q​
となるので，
点電荷の周りの電場
E(r)=14πε0qr2
E(r)=\dfrac{1}{4\pi\varepsilon_0}\dfrac{q}{r^2}
E(r)=4πε0​1​r2q​
がわかりました。
この表式より，電荷 QQQ の点電荷が，距離 rrr だけ離れた電荷 qqq を持つ点電荷から受けるクーロン力の大きさは
F=qE(r)=14πε0Qqr2
F=qE(r)=\dfrac{1}{4\pi\varepsilon_0}\dfrac{Qq}{r^2}
F=qE(r)=4πε0​1​r2Qq​
であることがわかります。
ちなみに導出でGaussの法則を用いましたが，これはMaxwell方程式という古典電磁気学の基本方程式の中の一つです。Maxwell方程式については，以下の記事で詳しく解説されています。

マクスウェル方程式

点電荷のポテンシャル(電位)

クーロン力がもとまったので，エネルギー積分を行うことで，点電荷のつくるポテンシャル(位置エネルギー)を求めることができます。
導出は以下の記事で詳しく解説されています。
電位の定義｜エネルギーとしての解釈・具体例

点電荷のつくる電位(無限遠基準)

$U(r)=\dfrac{1}{4\pi\varepsilon_0}\dfrac{q}{r}$

電位とは，単位電荷あたりの位置エネルギーなので，これに電荷の大きさ $Q$ をかけることで，位置エネルギーが表せます。

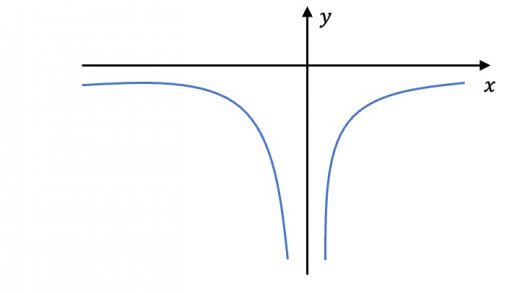
では，この電位をグラフに書いてみましょう。点電荷のポテンシャル点電荷の符号が正の時は，上のようなグラフになります。 $r\to0$ とすると，無限大に発散し， $r\to\pm\infty$ で0に収束します。

一方，点電荷の符号が負の時は，以下のようなグラフになります。点電荷の作る電位

点電荷の例題

例題

点電荷の例題上の図のように，正電荷 $q$ を持つ点電荷を $x$ 軸上 $a,-a$ に固定した。

(1) $x$ 軸上の座標点 $(x,0)$ の電位 $V(x)$ を $x$ の関数として求め，グラフをかけ。
(2) $x$ 軸上の $-a\leq x\leq a$ を満たすある点に，点電荷を置いた。この時，この点電荷はどのような運動をするか。

解答

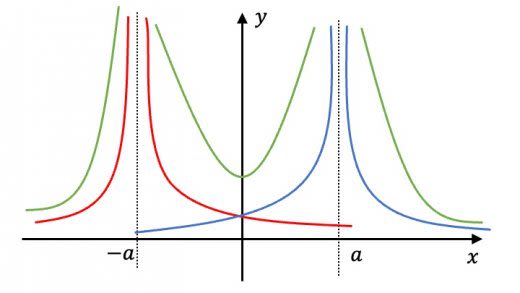(1) 電位のグラフ $-a$ にある点電荷による電位を赤で， $a$ にある点電荷の電位を青でグラフに書いた。これらを重ね合わせると，緑色のグラフになり，これが答えである。

(2) $-a\leq x\leq a$ 　における電位は，放物線のような形になっている。明かに，これは原点を中心とする周期運動を表している。

点電荷では物理量が発散します。このことは，量子力学で「くりこみ」という問題になって現れることになります。