流体(流動体)の定義｜粘性・粘性抵抗・粘性係数｜流体力学の基礎

更新 2021/10/13

この記事では，まず流体を定義して，流体に関する種々の概念を解説したのち，日常的な流体の例として空気を取り上げます。その後，流体力学の基本法則を紹介し，流体力学の世界を原理から理解することを目指します。

さまざまな種類の流体(流動体)

流体(流動体)とは，一般的に，空気や水などの気体や液体のことを総称する名詞です。
ミクロにみると，流体は多数の分子の集まりであり，それぞれの分子が，電磁気的な力によって相互作用している状態にあります。ニュートンの運動方程式では，3つ以上の分子の相互作用を一般的に解析することはできないので，流体中の多数の分子の運動を完全に解析することは当然不可能です。ただ，流体をマクロな観点で観察してみると，色々な性質が明らかになります。
また，流体といっても，気体と液体では性質が異なります。液体は圧縮するのに非常に大きな力が必要であり，圧力変化に対する体積変化を無視して考えることが多いです。それに対して，気体は，ピストンなどで力を加えると，容易に圧縮できます。液体のように圧縮が困難な流体を非圧縮性流体，気体のように圧縮が容易な流体を圧縮性流体といいます。

$$ a_{n}→ / alpha ⇒ a_{2n}→ /alpha $$ を数列のε論法で示す方法を教えてください。 2

【英語】姉は長年ペットを飼いたいと思っています。 My sister has wanted to have a pet 3

ろ過、蒸留、分留、クロマトグラフィー、ペーパークロマトグラフィー →分離ができる再結晶、昇華法 →分離と精製ができる 4

蒸留と分留の違いを教えてください。自分で調べてみたら、蒸留は液体と固体の混合物の分離で、分留は液体と液体の混合物の分離 5

粘性の定義・粘性抵抗・粘性係数・動粘性係数

流体の速度が流体の各点によって異なるとき，流体同士に摩擦力が生じることがわかっています。摩擦力が生じる流体の性質のことを粘性，生じる摩擦力のことを粘性抵抗といいます。粘性抵抗の性質を理解するために，以下の最も簡単な例を考えてみます。 name 距離 $h$ だけ離れた平板間に流体が満たされています。下の平行板を上の平行板に対して一定の速さ $v$ で上下の平行を保ちながら動かします。このとき流体は板と平行に流れます。各点での流速を $u(y)$ とすると，粘性抵抗は $q=\mu\dfrac{du}{dy}$ で与えられることが実験的にわかっています。ここで係数 $\mu$ を粘性係数といいます。粘性係数の単位は $\mathrm{N\cdot s/m^2=Pa\cdot s}$ です。また，粘性係数を流体の密度 $\rho$ で割った $\nu=\dfrac{\mu}{\rho}$ も流体運動の記述によく使われます。この $\nu$ のことを動粘性係数といいます。この世界のほとんどの流体では，粘性係数は定数とみなせることがわかっています。

流体の例〜空気・空気圧〜

流体には様々な種類があり，その代表例として空気が挙げられます。空気の及ぼす圧力はとても大きいのですが，空気が当たり前の存在すぎて，我々は日常生活でそのことにあまり気づきません。空気圧が大きいことを実感できる例を紹介します。

例題

下図のように水を満タンに入れたコップに，大きめの紙を一枚のせ，ひっくり返した。この時，コップの中の水はどうなるだろうか。 name

解答

コップと水，紙にかかる力がつりあうとして，それぞれのつりあいの式を書いてみる。 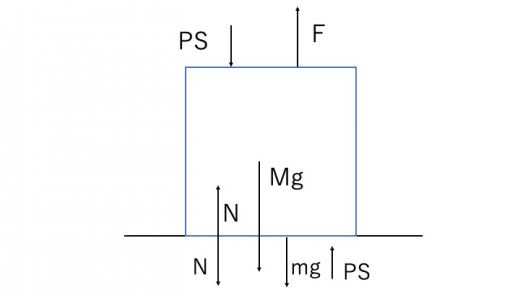name $F$ を手で加える外力， $pS$ を大気圧， $Mg,mg$ をそれぞれ水にはたらく重力と紙にはたらく重力， $N$ を垂直抗力とする。

コップと水 : $F-pS-Mg+N=0$

紙 : $pS-mg-N=0$

2式より $F=(M+m)g,N=pS-mg$ を得る。

$N\geqq0$ であるためには， $m\leqq\dfrac{pS}{g}\simeq\dfrac{1.0\times10^5\mathrm{N/m^2}\cdot(0.1\mathrm{m})^2}{10\mathrm{m/s^2}}=100\mathrm{kg}$

よって紙の質量が $100\mathrm{kg}$ 以下の時，紙は離れず，水はこぼれない。

なんとひっくり返しても(紙の質量が $100\mathrm{kg}$ 以下の時は)紙は落ちないという直感に反する結果を得ることができました。筆者が実際にやってみたところ，すごい光景を観察することができました。ぜひ実験してみてください。

流体に対して成立する定理

ベルヌーイの定理(ベルヌーイの法則)完全流体のエネルギー保存を表す，ベルヌーイの定理というものがあります。
ベルヌーイの定理
定常流では流線に沿って
12q2+U+∫dpρ=const.\dfrac{1}{2}q^2+U+\int\dfrac{dp}{\rho}=\mathrm{const.}21​q2+U+∫ρdp​=const.
が成り立つ。
ここで定常流とは流れの速度が一定の流体，qqq は流速，UUU は重力のポテンシャルエネルギー，ρ\rhoρ は流体の密度，ppp は流体の圧力を表す。P=∫dpρP=\int\dfrac{dp}{\rho}P=∫ρdp​ を圧力関数と呼ぶこともある。
ベルヌーイの定理の導出や詳しい解説については，以下の記事を参照してください。
オイラーの運動方程式・流線・ベルヌーイの定理の導出
オイラーの運動方程式ベルヌーイの定理は，流体力学の基礎方程式の1つである，オイラーの運動方程式のエネルギー積分と捉えることもできます。
オイラーの運動方程式
∂v∂t+(v⋅∇)v=X−∇pρ\dfrac{\partial\boldsymbol{v}}{\partial t}+(\boldsymbol{v}\cdot\nabla)\boldsymbol{v}=\boldsymbol{X}-\dfrac{\nabla p}{\rho}∂t∂v​+(v⋅∇)v=X−ρ∇p​
ここで v\boldsymbol{v}v は流体の速度ベクトル，X\boldsymbol{X}X は単位質量あたり，流体に働く外力，ρ\rhoρ は流体の密度，ppp は流体の圧力を表す。
式中の記号については，以下を参照してください。
ベクトル場における発散（div）と回転（rot）の定義・意味
勾配ベクトルの意味と例題
偏微分の意味と計算例・応用
オイラーの運動方程式は，ナビエ-ストークス方程式から粘性項を省いたもので，流体力学の基礎方程式の一つです。オイラー方程式を一般的に解くことは，ナビエ-ストークス方程式を一般的に解くことと同様に，超難問として知られています。
ナビエ-ストークス方程式は以下の記事で詳しく解説されているので，こちらをご覧ください。
ナビエ-ストークス方程式の導出
大学では，「流体力学」という学問で，オイラーの運動方程式やナビエ-ストークス方程式を用いて流体の運動を計算していきます。