パスカルの原理の導出と油圧機への応用
この記事では,流体の基本的な法則である,パスカルの原理について解説します。パスカルの原理は高校の教科書に載っていないことが多いですが,アルキメデスの原理とならぶ流体の基本法則の一つです。
パスカルの原理
パスカルの原理
流体が変形しない閉じた容器に入っているとする。流体が静止しているとき,流体に容器の外のある1点から圧力を加えると,流体全体のどの部分でも同じだけ圧力が増加する。
パスカルの原理は流体の基本原理として,広く知られています。この原理は、容器中の流体が液体のみの場合だけでなく,液体や気体が共存している場合にも適用することができます。
この記事に関連するQ&A
パスカルの原理と静水圧の一様等方性
パスカルの原理と静水圧の一様等方性
パスカルの原理は,より厳密に表現し直すと,以下のようになります。以下のパスカルの原理の表式は,静流体力学の基本法則として知られています。
流体の微小定積要素 を考える。流体の密度を ,圧力を ,微小流体に加わる単位質量あたりの外力を とすると,
が成り立つ。

微小流体の内側から外側の向きの単位法線ベクトルを とする。(圧力の向きと逆であることに注意)微小流体の表面 にかかる力 は で与えられる。この式にガウスの定理(以下の補足を参照)を用いると, また,流体は静止しているので,力のつりあいより, を用いて が成り立つ。
よって 以上より を得る。
ガウスの定理の表式 において,定ベクトル とスカラー を用いて として左辺にまとめると, となる。 は任意のベクトルなので, となる。
定理の中では,この形の式を用いています。
ガウスの定理については,以下の記事で詳しく解説されていますので,こちらをご覧ください。
静流体の平衡式は,加わる外力がそのまま の変化になり,圧力の変化が流体中に伝播していくイメージです。例えば外力がない時は となり,圧力はどの部分でも同じことがわかります。
また,証明では,静水圧の一様等方性を用いています。静水圧の一様等方性は,実は水以外の流体でも成り立ちます。
静水圧について,静止した水のある1点における圧力はどの方向でも等しい
静水圧の一様等方性の導出については,以下の記事をご覧ください。
静水圧の一様等方性やパスカルの原理の導出には,流体の定義である
静止流体では,流体の内力は接触面に平衡な成分(接線応力)を持たない
が用いられています。
パスカルの定理の応用〜油圧機〜
パスカルの定理の応用〜油圧機〜
パスカルの定理を用いることで,小さな力で重いものを持ち上げることができます。この方法は,油圧機などに応用されています。以下で原理を詳しくみてみましょう。
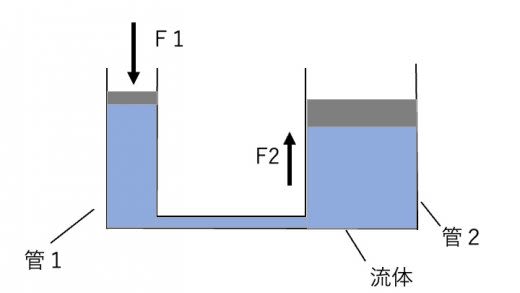 図のように断面積 の管1と,断面積 の管2が細い管で繋がった装置を考えます。装置には流体が含まれているとします。ここで管1を力 で押すと,流体の圧力は だけ増えます。そうすると,パスカルの原理より,圧力の増分は流体の各点で等しいので,管2にも圧力 がかかります。このとき,
管2の上面にかかる力は となります。
図のように断面積 の管1と,断面積 の管2が細い管で繋がった装置を考えます。装置には流体が含まれているとします。ここで管1を力 で押すと,流体の圧力は だけ増えます。そうすると,パスカルの原理より,圧力の増分は流体の各点で等しいので,管2にも圧力 がかかります。このとき,
管2の上面にかかる力は となります。
例えば とすると, の 倍の大きさの力が管2の上面にかかることになります。小さな力を加えるだけで,重いものを動かしたり,持ち上げたりできることになります。このような,パスカルの原理を応用した油圧機は,ブレーキやジャッキに用いられています。
よくあるパスカルの原理の誤解
よくあるパスカルの原理の誤解
パスカルの原理では一見,流体にはたらく圧力はどこでも等しいと誤解してしまいそうです。しかしパスカルの原理では 流体にはたらく圧力の大きさではなく,流体にはたらく圧力に「増え幅」に着目しています。つまりパスカルの原理は,流体圧がどこでも等しいことではなく,容器の外から力を加えたとき,その増え幅がどこでも等しいことを述べていることに注意してください。
パスカルの原理の他にも,物体にかかる流体圧の合力の求め方としては,アルキメデスの原理などがあります。アルキメデスの原理については,以下の記事を参照してください。
パスカルの原理は古典的な法則にもかかわらず,現在でも油圧機などに応用されていることから,その重要性がわかります。











