ドップラー効果の原理・公式・応用例

更新 2021/09/07

ドップラー効果(もしくはドップラーシフト)の原理や公式の導出，応用例について解説します。

ドップラー効果とは，媒質に対して波源や観測者が運動するとき波動の振動数が変化する現象であり，日常生活から宇宙まであらゆる場所で起きています。

波源と観測者が動く場合のドップラー効果の公式

$f' = \frac{c \pm v_o}{c \pm v_s}f$

ドップラー効果が現れる現象

皆さんは日常生活で次のような事を経験したことがあるのではないでしょうか？
救急車が自分に近づいて来るときサイレンの音が高く聞こえ，逆に遠ざかるとき低く聞こえる
F1レースカーがテレビカメラに近づいて来るときエンジンの音が高く聞こえ，逆に遠ざかるとき低く聞こえる
実はこれらは音のドップラー効果によるものなのです。
ドップラー効果は日常生活に限ったものではありません。
例えば次のような問題を考えてみましょう。
遠くにある雨雲の動きを観測するにはどうすればいいか？
病気の人を傷つけずに臓器のはたらきや血流を調べるにはどうすればいいか？
遠くにある天体が地球に近づいているのか遠ざかっているのかを調べるにはどうすればいいか？
このような幅広い場面でも実はドップラー効果が関わっています。
この記事でドップラー効果について学び，日常生活から宇宙に至るまであらゆる現象が統一的に説明されるということを味わってみて下さい。

数学の問題です。 $xy$平面上で、原点$O(0,0)$、点$A(6,0)$、点$B(6,6)$、点$C(0,6)$を頂 2

流体力学について詳しい方がいたらお答えください 3

中1です。主語が三人称単数の疑問文、否定文のとき動詞は原型ですか？ 4

5.は右のように訳されているのですがalthoughとofはどのような意味の役割をしているのでしょうか？ 8.でlist 5

ドップラー効果の原理

ドップラー効果とはある媒質中に周波数 fff の波源を用意し，そこから離れた場所でその波動を観測することを考えます。
波源や観測者が媒質に対して動いているとき，実際に観測される周波数 f′f'f′ はもとの周波数 fff と異なってしまいます。これがドップラー効果です。
ある媒質中の波動の伝播速度を ccc，周波数を fff，波長を λ\lambdaλ とすると，c=fλc = f\lambdac=fλ という関係があるのでした。
このことに注意しつつ，ドップラー効果がなぜ起きるのかを解説していきます。
波源が動く場合まず比較のため波源が静止している場合を考えましょう。
時刻 t=0t=0t=0 に波動が発せられて，
時刻 t=Δtt=\Delta tt=Δt にその波動が観測されたとします。
その様子は下図のようになります。
(図では簡単のため1波長分だけ描きました)
これに対し波源が動いている場合を考えましょう。
同じく時刻 t=0t=0t=0 に波動が発せられ，
波源は観測者に向かって速度 vsv_svs​ で動いていたとします。
すると時刻 t=Δtt=\Delta tt=Δt に波動は観測者に到達しますが，
図の波動の右端は vsΔtv_s\Delta tvs​Δt 分だけ観測者側にずれてしまいます。
この分だけ波長は短くなるのです！
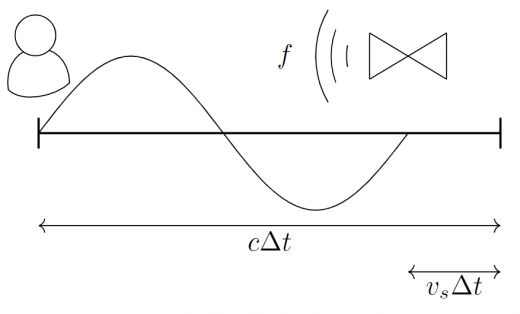
波源が静止している場合と動いている場合での波長の比を考えれば
λ′=cΔt−vsΔtcΔtλ=c−vscλ
\begin{aligned}
    \lambda'
    = \frac{c\Delta t - v_s\Delta t}{c\Delta t}\lambda
    = \frac{c-v_s}{c}\lambda
\end{aligned}
λ′=cΔtcΔt−vs​Δt​λ=cc−vs​​λ​
が成り立ちます。
更に関係式 c=fλc=f\lambdac=fλ を用いると
f′=cc−vsf
\begin{aligned}
    f' = \frac{c}{c-v_s}f
\end{aligned}
f′=c−vs​c​f​
が成り立ちます。
救急車のサイレンで経験しているように，
波源が近づいて来ると周波数が高くなることが分かりますね。
逆に波源が観測者から遠ざかって行く場合は，
図の波動の右端は vsΔtv_s\Delta tvs​Δt 分だけ観測者と反対側にずれるので
f′=cc+vsf
\begin{aligned}
    f' = \frac{c}{c+v_s}f
\end{aligned}
f′=c+vs​c​f​
が成り立ちます。
波源が遠ざかって行くと周波数が低くなることが分かりますね。
観測者が動く場合まず比較のため観測者が静止している場合を考えましょう。
今度は時刻 t=0t=0t=0 にその波動が観測者に到達したとします。
そのまま観測を続け t=Δtt=\Delta tt=Δt になるまでに，
媒質が何回振動したかを数えることで，
観測者は周波数が fff だと分かります。
下図は観測した波動が観測者の後ろに通過した様子です。
(ここでも簡単のため1波長分だけ描きました)
これに対し観測者が動いている場合を考えましょう。
観測者は波源に向かって速度vov_ovo​で動いていたとします。
すると観測者は下図のように，voΔtv_o\Delta tvo​Δt だけ右に動いた分，余分に媒質の振動を数えてしまいます！
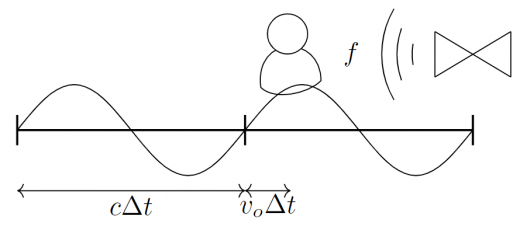
観測者が静止している場合と動いている場合で，
観測される媒質の振動回数の比を考えれば
f′=cΔt+voΔtcΔtf=c+vocf
\begin{aligned}
    f'
    = \frac{c\Delta t+v_o\Delta t}{c\Delta t}f
    = \frac{c+v_o}{c}f
\end{aligned}
f′=cΔtcΔt+vo​Δt​f=cc+vo​​f​
が成り立ちます。
観測者が波源に向かって動くと，
周波数が高くなることが分かりますね。
逆に観測者が波源から遠ざかって行く場合は，
観測者が左に動いた分媒質の振動を数えられなくなってしまうので
f′=c−vocf
\begin{aligned}
    f' = \frac{c-v_o}{c}f
\end{aligned}
f′=cc−vo​​f​
が成り立ちます。
観測者が波源から遠ざかって行くと周波数が低くなることが分かりますね。

種々の公式の導出

波源が観測者に対して斜めに動く場合

下図のように波源が観測者に対して見込み角 $\theta$ の位置にあり，左方向に速度 $v_s$ で動いている場合を考えます。 doppler_07 速度ベクトルを分解すると，波源は観測者に対して $v_s\cos\theta$ で近づいているものと見なせます。「ドップラー効果の原理」で導いた式を用いれば，以下の公式が成り立ちます。

斜めドップラー効果

$\begin{aligned} f' = \frac{c}{c-v_s\cos\theta}f \end{aligned}$

実はこの式はホイヘンスの原理を使って示すこともできるので，考えてみるのも楽しいでしょう。

波源と観測者が共に動く場合

波源の速度を $\pm v_s$ (観測者から遠ざかる方向を正)，観測者の速度を $\pm v_o$ (波源に近づく方向を正)とします。このような場合，波源が動くことにより波長が変化した波動について，更に動いている観測者が媒質の振動回数を観測することになります。「ドップラー効果の原理」で導いた式を用いれば $\begin{aligned} f' = \frac{c\pm v_o}{c}\frac{c}{c\pm v_s}f \end{aligned}$ が成り立ちます。式を整理すると以下の公式が成り立ちます。

波源と観測者が動く場合のドップラー効果

$\begin{aligned} f' = \frac{c \pm v_o}{c \pm v_s}f \end{aligned}$

符号の丸暗記をする必要はありません。波源や観測者の速度によって周波数が高くなるはずなのか低くなるはずなのかを，定性的に理解していれば符号はその場で判断できます。

また，ドップラー効果が波長の変化によって引き起こされているのか，実際に数えられる媒質の振動回数の変化によって引き起こされているのかを理解していれば，分母/分子のどちらに $v_s/v_o$ が来るのかも判断できます。

ここで，上の式が波源と観測者の相対速度 $v_s-v_o$ では書けていないことに注意しましょう。これはドップラー効果が波源と観測者の間の二体問題ではないということを意味します。実際に今までの議論は全て媒質の静止系でしか成り立っていません。

媒質が動く場合

媒質が動いている場合は，今までの議論が使える媒質の静止系に移れば良いです。媒質の速度が $w$ ( $v_{s},v_o$ に合わせて正負を選ぶ)であったとき，媒質の静止系にいる観測者にとっては波動の伝播速度が $c$ ，波源の速度が $v_s-w$ ，観測者の速度が $v_o-w$ に見えます。「波源と観測者が動く場合のドップラー効果」の式を用いれば，以下の公式が成り立ちます。

媒質が動く場合のドップラー効果

$\begin{aligned} f' = \frac{c \pm (v_o-w)}{c \pm (v_s-w)}f \end{aligned}$

ドップラー効果の応用

応用例今まで波源や観測者が動くことで波動の周波数が変化するということを見てきましたが，これを逆に利用すれば波動の周波数の変化を見ることで波源や観測者の動きを計測できることになります。
例えば，雨雲に向かって電磁波を照射してその反射波の周波数の変化を観測すれば，雨雲の動きについて知ることができます。
人の臓器に向かって超音波を照射してその反射波の周波数の変化を観測すれば，臓器や血流の様子について知ることができます。
また，遠くにある天体が出しているはずの電磁波の周波数が変化して見えたのであれば，その天体の運動について知ることができます。
より発展した話題興味のある読者の方に向けて，いくつかより発展した話題をご紹介します。
以下のことについて考えてみると，きっと面白いことがあると思います。
電磁波には"媒質"があるのか？
電磁波のドップラー効果の式は上のもので本当に十分だろうか？
波源や観測者の速度が波動の伝播速度を超えてしまったら何が起きるか？
入試問題だけを見ていると，なぜこんなややこしい設定の問題を考えるのかと感じてしまうかもしれません。
しかしドップラー効果は日常生活から宇宙まで幅広い場面で起きていて，様々な重要問題と結びついています。
ぜひドップラー効果について学んだことを生かせないか色々考えてみて下さい。