赤方偏移・光のドップラー効果

更新 2021/03/28

←前の記事　後の記事→
Einsteinの一般相対性理論は本当に正しいのか？という疑問を持たれた方もいるかもしれません。一般相対性理論は
重力による光の湾曲
水星の近日点移動
赤方偏移
などによってその正しさが認められています。古典力学ではどうしてもうまく説明できなかった現象が，一般相対性理論では
説明できてしまうのです。その一例として，赤方偏移を取り上げてみます。

エッセンス熱力学の問題です 2枚目の解き方がダメな理由が分かりません、誰か教えて頂けませんか……？正しい答えは58/9 2

消費される電力の合計がいくらかという問題です。電球に使われるフィラメントのように，電流によって温度が大きく変化する導 3

エッセンスから熱力学の問題です。この問題の解き方が2枚目じゃダメな理由教えてくださるとものすごく助かります…… 正しい 4

ケトンやアルデヒドには水素が付加(というか還元される)しますが、カルボン酸には水素は付加しないのですか？理由も教えてくだ 5

重力による赤方偏移

原点に星があって，その星が重力場を作っているとします。つまり，Schwarzschild解が適用できる状況を考えます。
星から aaa だけ離れた静止点 AAA での計量テンソルを gμν(A)g_{\mu\nu}(A)gμν​(A)，
星から bbb だけ離れた静止点 BBB での計量テンソルを gμν(B)g_{\mu\nu}(B)gμν​(B) とすると，
→一般相対性理論における固有時の節「重力による伸び縮み」における式：
dτ=−g00dt
d\tau = \sqrt{-g_{00}} dt 
dτ=−g00​​dt
により，
dτA=−g00(A)dtA=1−2madtAdτB=−g00(B)dtB=1−2mbdtB\begin{aligned}
       d\tau_A &= \sqrt{-g_{00}(A)} dt_A = \sqrt{1 - \dfrac{2m}{a}}dt_A\\
       d\tau_B &= \sqrt{-g_{00}(B)} dt_B = \sqrt{1 - \dfrac{2m}{b}}dt_B
\end{aligned}dτA​dτB​​=−g00​(A)​dtA​=1−a2m​​dtA​=−g00​(B)​dtB​=1−b2m​​dtB​​
と表せます。ここで，dtA,dtBdt_A, dt_BdtA​,dtB​ は一般座標に変換する前の局所慣性系での微小時間間隔であるとします。
一旦，重力場がない場合の光の周期を考えます。星のある場所から，周期 Δt\Delta tΔt の光を発したとすると，
重力場がなければ，AAA の観測者が計っても，BBB の観測者が計っても周期は Δt\Delta tΔt となるはずです。
重力場があるときは，周期は A,BA,BA,B それぞれの固有時で計った周期で観測されます。A,BA,BA,B で観測される周期を，
ΔτA,ΔτB\Delta \tau_A, \Delta \tau_BΔτA​,ΔτB​ とすれば，
Δt=1−2maΔtΔt=1−2mbΔt\begin{aligned}
       \Delta t &= \sqrt{1 - \dfrac{2m}{a}} \Delta t\\
       \Delta t &= \sqrt{1 - \dfrac{2m}{b}} \Delta t
\end{aligned}ΔtΔt​=1−a2m​​Δt=1−b2m​​Δt​
よって，A,BA,BA,B で観測される光の振動数を νA,νB\nu_A,\nu_BνA​,νB​ とすると，
νAνB=ΔτBΔτA=1−2mb1−2ma
       \dfrac{\nu_A}{\nu_B} = \dfrac{\Delta \tau_B}{\Delta \tau_A} = \sqrt{\dfrac{1 - \dfrac{2m}{b}}{1 - \dfrac{2m}{a}}}
νB​νA​​=ΔτA​ΔτB​​=1−a2m​1−b2m​​​
となります。a<ba< ba<b なら，νB<νA\nu_B < \nu_AνB​<νA​ となり，波長は AAA より BBB の方が長くなります。これを，重力による赤方偏移と呼びます。

光のDoppler効果

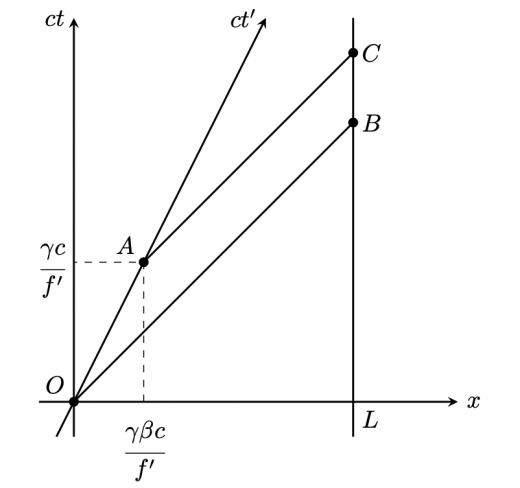
慣性系 SSS で光源が速度 vvv で +x+x+x 方向に動いている状況を考えます。詳しい状況は上図
を参照してください。SSS の x=Lx = Lx=L にいる観測者は，光源を観測します。光源は，光源の静止系 S′S'S′ において，1f′\dfrac{1}{f'}f′1​ 秒ごとにフラッシュするとします。
つまり，OAOAOA 間は，
t′=1f′
       t' = \dfrac{1}{f'}
t′=f′1​
の時間間隔があるとします。OOO でフラッシュした光は傾き1の OBOBOB を通って BBB に達します。AAA でフラッシュした光は傾き1の ACACAC を通って CCC に達します。
このとき，BCBCBC 間の時間間隔 1c=Δt\dfrac{1}{c} = \Delta tc1​=Δt を求めることを考えましょう。
これが SSS 系における周期に対応します。
AAA の S′S'S′ における座標は (t′,x′)=(1f′,0)(t',x') = (\dfrac{1}{f'}, 0)(t′,x′)=(f′1​,0) より，ローレンツ変換を適用すれば，AAA の SSS における座標は
{ct=γcf′x=γβcf′=γvf′
       \begin{cases}
              ct = \dfrac{\gamma c}{f'}\\
              x = \dfrac{\gamma \beta c}{f'} = \dfrac{\gamma v}{f'}
       \end{cases}
⎩⎨⎧​ct=f′γc​x=f′γβc​=f′γv​​
で表せます。よって SSS の座標 (t,x)(t,x)(t,x) で B,CB,CB,C を表すと，
B(Lc,L),   C(γf′+Lc−γvf′c,L)
       B\left(\dfrac{L}{c}, L\right), ~~~ C\left(\dfrac{\gamma}{f'} + \dfrac{L}{c} - \dfrac{\gamma v}{f'c}, L\right)
B(cL​,L),   C(f′γ​+cL​−f′cγv​,L)
これより，
1f=Δt=(γf′+Lc−γvf′c)−Lc=γf′(1−vc)=1−vc1+vc 1f′
       \dfrac{1}{f} = \Delta t = \left(\dfrac{\gamma}{f'} + \dfrac{L}{c} - \dfrac{\gamma v}{f'c}\right) - \dfrac{L}{c} = \dfrac{\gamma}{f'}\left(1 - \dfrac{v}{c}\right) = \sqrt{\dfrac{1-\dfrac{v}{c}}{1+\dfrac{v}{c}}}~\dfrac{1}{f'}
f1​=Δt=(f′γ​+cL​−f′cγv​)−cL​=f′γ​(1−cv​)=1+cv​1−cv​​​ f′1​
1−vc1 - \dfrac{v}{c}1−cv​ は古典的なDoppler効果でもみられた成分ですが，γ\gammaγ がかかっているのが相対論的な効果であると言えます。
重力による赤方偏移と光のDoppler効果を合わせたものが，実際に観測される赤方偏移となります。
←前の記事　後の記事→

この記事の監修者

でーちー

公立地方進学校出身。高校時代は部活動に勤しみ，合間を縫って勉強を進めた。受験生時代には毎日12時間以上の勉強を続け，東京大学理科一類に現役合格。大学でも数学・物理を得意とし，情報系の学科に進みつつも，独学で勉強を続けている。学びTimesでは主に「高校数学の美しい物語」「高校生から味わう理論物理入門」の記事執筆・修正業務に尽力している。