ブラッグ反射とラウエ斑点の原理解説

まず, 下図のような3次元的に周期配列した結晶を考えます。これは, 平面に原子が配列した面を積み重ねたしたものとして考えることができます。この2次元の面を格子面といい, 格子面間隔を $d$ とします。

この結晶にX線を照射すると, X線が特定の入射角や波長の大きさの場合に, 鏡のようにX線が反射します。ある条件のときだけ反射光が大きくなるようなイメージでOK。

ブラッグの反射条件(ブラッグの法則)

X線の入射角 $\theta$ や波長 $\lambda$ がある条件を満たしたとき, 大きく反射する時の条件をブラッグの反射条件(ブラッグの法則)といい,　次の式で表すことができます。このときの反射を, ブラッグ反射と呼びます。

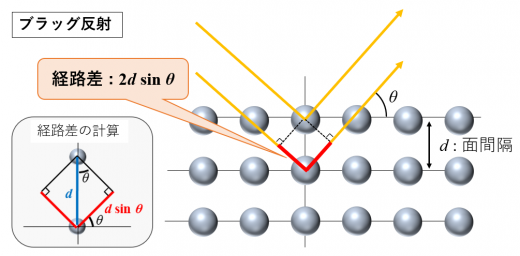
格子面nとn+1における経路差(光路差)は左の図のように幾何学的に計算され, 経路差は $2d \sin{\theta}$ となります。

ブラッグ反射はヘンリー・ブラッグ(英, 1862-1942), ローレンス・ブラッグ(英, 1890-1971)の親子によって発見されました。1915年にブラッグ父子はブラッグ反射に関する功績でノーベル物理学賞を受賞しました。

波が強め合う条件

「X線が特定の入射角や波長の場合に鏡のようにX線が反射する」とは, つまりある波長やある入射角で波の干渉(強め合い)が起きているということです。

ブラッグの反射条件にもあるように, 波の干渉は結晶構造の格子面nの反射波と格子面n+1の反射波で生じています。

波の干渉や波の性質について, 不安な方は以下の記事で復習してみてください。

→波の干渉・回折

→波の重ね合わせ

X線散乱における前提事項

まず, 結晶にX線を入射する時の前提事項を2つ確認します。

• X線は高い透過性を持つ → 結晶の奥の方までX線が入り込む

• ある原子に対する入射角と反射角は同じ(位相が等しい)

ここで「常に反射が起こっているのに, なぜブラッグ反射(特定の条件での強め合い)が必要なのか」と思う方がいるかもしれません。

その回答はポイントが3つあります。

1. 今回は結晶構造を考えており, 結晶の表面(格子面n)と奥(格子面n+1)の反射波の位相がずれる

2. 位相がずれた波の合成波は減衰する

3. 位相がそろった合成波は強め合い, ブラッグ反射となる

→位相

上記のことを理解することがブラッグ反射最大のポイントです。これを理解するために, X線の波長を固定し, X線の入射角を変化させながら考えていきます。

「経路差＝波長の自然数倍」で干渉する原理

ブラッグの条件で干渉が起こる原理を丁寧に説明していきます。

X線の波長を固定し, 入射角をだんだん大きくすることを考えます。入射角を大きくしていくと, 格子面nと格子面n+1の経路差はだんだんと大きくなります。

※経路差のことを光路差と表現する教科書もあります。

[補足] 経路差は $d \sin{\theta}$ で表され, $0 \leq \theta \leq \dfrac{\pi}{2}$ において角度が大きくなれば, 経路差 $d \sin{\theta}$ が大きい値を取るので,入射角が大きいほど, 経路差が大きくなることが納得できると思います。

ブラッグ反射の条件：経路差＝波長の自然数倍

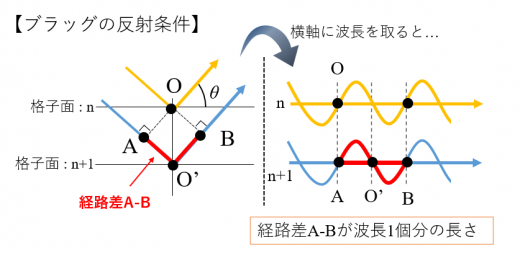
そして, ある入射角で2本のX線が強め合い干渉を起こします。その条件が, 「経路差が波長の整数倍になるとき」です。それ以外の角度では, 波を重ね合せても強め合いません。

このことを表現したのがブラッグの反射条件 $2d \sin{\theta} = n \lambda$ $(n = 1, 2, 3, \cdot \cdot \cdot )$　です。

経路差が波長の自然数倍で強め合うため, 入射角度を操作すれば $n=1$ のとき, $n=2$ のとき, $n=3$ のときと, 干渉が何度か見えます。

X線の入射角度を固定し波長の大きさを調整する場合についても, 固定された経路差に波長の整数倍が一致するときに干渉が起こります。

X線が透過しやすい結晶に連続X線を照射し, X線フィルムを置くと多くの斑点が観測されます。この斑点をラウエ斑点といいます。

斑点が映った写真をラウエ写真といい、この写真を撮影する以下の手法はラウエ法と呼ばれます。

ラウエ斑点は, 1912年にラウエ(独, 1879-1960)によって発見されました。この発見はX線が電磁波であることの証明に繋がりました。

ラウエはX線回折現象の功績により, 1914年にノーベル物理学賞を受賞しました。

ラウエ斑点とブラッグの条件

ブラッグ反射の条件の通り, X線を結晶に照射したとき特定の波長の場合でしか回折が起こりません。

しかし, ラウエは波長が連続的な連続X線を用いることで, 連続した波長 $\lambda$ (様々な波長を含むX線)の中で, 波長がブラッグの条件

$$2d \sin{\theta} = n \lambda$$

を満たす $\lambda$ のときに回折現象が起こります。ラウエ斑点では波長を固定していないため, 回折が起きている条件を決定することができないのが肝です。

ラウエ写真に写る斑点は物質の結晶構造(原子配列のパターン)で異なります。