等加速度系の変換〜リンドラー変換〜

重力がない空間を考えます。このとき，ここに静止したある慣性系 $S$ をとれます。これに対し，等加速度系 $S'$ は，$+x (+x')$ 向きに 加速度をもって等加速度運動をしながら進んでいるとします。さらに，$t = t' = 0$ において $S, S'$ の原点は重なるものとします。 互いの系にとって，相手の系が近づいてきて再び離れていくように見えるということです。ちょうどボールの投げ上げ運動のような 状況です。$S'$ 系からみて，$S$ は相対加速度 $g$ で近づいてきて，離れていくとします。

ある瞬間においては，慣性系 $S$ からみて，$S$ の原点から $S'$ の原点までの距離を $x(t)$ とします。この $t$ による 2階微分 $$a(t) = \dfrac{d^2 x(t)}{dt^2}$$ に対し，加速度の変換公式を使って（慣性系 $S$ に対して，$S'$ は瞬間的には一定速度であり，その瞬間は $v(t) = \dfrac{dx(t)}{dt}$ で動く慣性系とみなせるので，公式を利用することができます）， $S'$ からみた $S$ の原点から $S'$ の原点までの距離の2階微分は $$a'(t) = \dfrac{\left(1 - \dfrac{v_x^2}{c^2}\right)^\frac{3}{2}}{\left(1 - \dfrac{v_x^2}{c^2}\right)^3}a(t) = \left(1 - \dfrac{v_x^2}{c^2}\right)^{-\frac{3}{2}}a(t)$$ これが $S'$ からみた $S$ の加速度 $g$ に等しくなります。 $$\left(1 - \dfrac{v_x^2}{c^2}\right)^{-\frac{3}{2}}a(t) = g$$ $t$ で積分して， $$\dfrac{v(t)}{\sqrt{1 - \dfrac{v(t)^2}{c^2}}} = gt + C_1$$ $t = 0$ のとき $v(0) = 0$ より，$C_1 = 0$ $$v(t) = \dfrac{gt}{\sqrt{1 + \left(\dfrac{gt}{c}\right)^2}}$$ $t$ で積分して， $$\therefore x(t) = \dfrac{c^2}{g} \left(1 + \dfrac{g^2 t^2}{c^2}\right)^{\frac{1}{2}} + C_2$$ $t = 0$ のとき $x(0) = 0$ より，$C_2 = -\dfrac{c^2}{g}$ $$\therefore x(t) = \dfrac{c^2}{g} \left(1 + \dfrac{g^2 t^2}{c^2}\right)^{\frac{1}{2}} + -\dfrac{c^2}{g}$$ 今は，$S$ からみた $S'$ の原点を追いかけていたので，これは $tx$ 平面で $t'$ 軸を表す方程式です。$\alpha = \dfrac{g}{c^2}$ とすれば， $$x(t) = \dfrac{1}{\alpha}\left(1 + \alpha^2 (ct)^2\right)^\frac{1}{2} - \dfrac{1}{\alpha} \tag{1}$$ この $t'$ 軸にめもりをふることを考えましょう。$t'$ 軸は $x' = 0$ の世界線なので，$S'$ では静止しているため， 原点に置かれた時計は固有時を刻みます。よって $S$ 系で固有時を計算することを考えます。$S$ 系は慣性系なので， $$d\tau = \sqrt{1 - \dfrac{v(t)^2}{c^2}} dt$$ と表せるから， $$\begin{aligned} T' &= \int_0^T \sqrt{1 - \dfrac{v(t)^2}{c^2}}dt = \int_0^T \dfrac{v(t)}{gt}dt \\ &= \int_0^T \dfrac{1}{\sqrt{1 - \dfrac{v(t)^2}{c^2}}}dt = \dfrac{c}{g}\sinh^{-1}\left(\dfrac{g}{c}T\right) \end{aligned}$$ ただし，$T,T'$ は $S',S$ での時間間隔です。つまり， $$ct' = \dfrac{1}{\alpha} \sinh^{-1}(\alpha ct) \iff \dfrac{1}{\alpha} \sinh (\alpha ct') = ct$$ これを，式 $(1)$ に入れて整理すれば， $$x = \dfrac{1}{\alpha}\cosh (\alpha ct') - \dfrac{1}{\alpha}$$ よって，$(ct',0)$ で表される $t'$ 軸上の点に対応する $(ct,x)$ は， $$\begin{cases} ct = \dfrac{1}{\alpha} \sinh (\alpha ct')\\ x = \dfrac{1}{\alpha}\cosh (\alpha ct') - \dfrac{1}{\alpha} \end{cases} \tag{2}$$ で表されます。

一般の $(ct,x), (ct',x)$ で表される任意のイベントを考えます。もし，このイベントの瞬間，$S'$ が加速をやめたとすると，$S'$ は 慣性系となります。このイベントからは $S'$ における同時刻線は直線で表されます。もし同時刻線が加速中は曲がっていたとしたら， 加速が消えた瞬間に，曲がっていた線上のイベントが同時刻であったのに，いきなり直線上のものが同時刻であることに変わってしまうのです。 つまり，未来や過去にあったはずのイベントが，いきなり「今」になってしまい，「今」であったはずのものがいきなり未来や過去になってしまう ということである。これはあまりにも現実離れしているし，いまだかつて過去や未来の事象が現実で観測されたことはないはずです。 よってこれはありえないので，同時刻線は直線になります。

さて，$t'$ 軸上のある点 $(ct', 0)$ をとることを考えます。$S$ では $(ct,x)$ と表されたとします。このとき，$(ct,x)$ における $t'$ 軸 の傾き $\displaystyle \dfrac{d(ct)}{dx} = \dfrac{dw}{dx}$ は， $$\begin{aligned} \dfrac{dw}{dx} &= \dfrac{\dfrac{dw}{d(ct')}}{\dfrac{dx}{d(ct')}} = \dfrac{\cosh (\alpha ct')}{\sinh (\alpha ct')}\\ &= \dfrac{\alpha x + 1}{\alpha ct} = \dfrac{x + \dfrac{1}{\alpha}}{ct} \end{aligned}$$ となります。特殊相対論において，慣性系では傾き1の線に対して，$t'$ 軸と $x$ 軸は対称であることをすでに確認しています。 $(ct', 0)$ において，$S'$ 系は瞬間的に慣性系であることより，$(ct',0)$ 近傍では，$t'$ 軸と同時刻線が，傾き1の線に対して， 対称に交わるはずです。よって，$(ct',0)$ の近傍においては，同時刻線は傾き $\dfrac{ct}{x + \dfrac{1}{\alpha}}$ の 直線として表されます。$(ct',0)$ にはとても短い傾き $\dfrac{ct}{x + \dfrac{1}{\alpha}}$ の線分がひけて，それが 同時刻線であるということです。同時刻線は直線であることを前段落で確認しています。よってこの線分は直線として無限に引き伸ばすことができます。

さて，$\left(ct = 0, x = - \dfrac{1}{\alpha}\right)$ から $(ct,x)$ に直線を引いた時，この線の傾きは $$\dfrac{ct-0}{x - \left( -\dfrac{1}{\alpha}\right)} = \dfrac{ct}{x + \dfrac{1}{\alpha}}$$ です。したがって，まさにこの直線が同時刻線になります。

では，一般に $(ct',x')$ の点をとります。$S$ 系では $(ct,x)$ と表されるとしましょう。

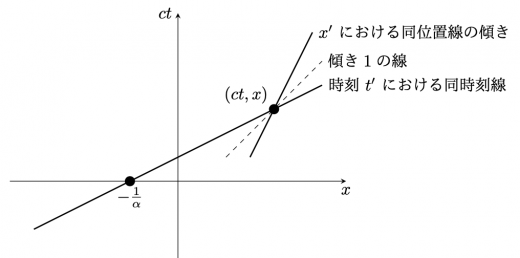
上図を参照してください。$(ct,x)$ の近傍でも，同時刻線と同位置線は傾き1の線に対して対称です。このとき，$x = x'$ で一定の線の傾きは， $$\dfrac{x + \dfrac{1}{\alpha}}{ct}$$ よって，同位置線というのは，$(ct,x)$ においては傾きが $\displaystyle\dfrac{d(ct)}{dx}$ が $$\dfrac{d(ct)}{dx} = \dfrac{x + \dfrac{1}{\alpha}}{ct}$$ で表される曲線です。これを微分方程式とみて解けば， $$\begin{aligned} (ct) d(ct) &= \left(x + \dfrac{1}{\alpha}\right) dx\\ \dfrac{1}{2}(ct)^2 &= \dfrac{1}{2}x^2 + \dfrac{x}{\alpha} + C \end{aligned}$$ ここで $C$ は積分定数です。$t = t' = 0$ において $x = x' = X$ であるような点を通るとすれば， $$\begin{aligned} 0 &= \dfrac{1}{2}x^2 + \dfrac{x}{\alpha} + C\\ C &= -\dfrac{1}{2}x^2 - \dfrac{x}{\alpha} \end{aligned}$$ したがって， $$\begin{aligned} \dfrac{1}{2}x^2 + \dfrac{x}{\alpha} - \dfrac{1}{2}(ct)^2 &= \dfrac{1}{2}x^2 + \dfrac{x}{\alpha}\\ \left(x + \dfrac{1}{\alpha}\right)^2 - (Ct)^2 &= \left(X + \dfrac{1}{\alpha}\right)^2 \end{aligned}$$ これは $X$ を動かせば $$\begin{cases} y = x + \dfrac{1}{\alpha}\\ y = -x - \dfrac{1}{\alpha} \end{cases}$$ を漸近線とする双曲線の集まりを表します。媒介変数 $\theta$ を用いれば， $$\begin{cases} x + \dfrac{1}{\alpha} = \left(X + \dfrac{1}{\alpha}\right) \cosh \theta\\ ct = \left(X + \dfrac{1}{\alpha}\right) \sinh \theta \end{cases}$$ と表せます。$X = 0$ としたとき， $$\begin{cases} x = \dfrac{1}{\alpha}\cosh \theta - \dfrac{1}{\alpha}\\ ct = \dfrac{1}{\alpha} \sinh \theta \end{cases}$$ であり，これは式 $(2)$ に等しいはずですから，$\theta = \alpha ct'$。よって， $$\begin{cases} x = \left(X + \dfrac{1}{\alpha}\right) \cosh \alpha ct' - \dfrac{1}{\alpha}\\ ct = \left(X + \dfrac{1}{\alpha}\right) \sinh \alpha ct' \end{cases}$$ を得ます。この変換をRindler変換と呼ぶことがあります。

変換式を全微分すると， $$\begin{cases} dx = \cosh (\alpha ct') dx' + (\alpha x' + 1)\sinh (\alpha ct') d(ct')\\ d(ct) = \sinh(\alpha ct')dx' + (\alpha x' + 1)\cosh (\alpha ct')d(ct') \end{cases}$$

これを， $$ds^2 = -c^2 dt^2 + dx^2 + dy^2 + dz^2$$ に代入すると（$dy,dz$ については，$S'$ 系が局所的に慣性系であり，慣性系同士の変換「ローレンツ変換」において $y,z$ が変化しなかったことから $dy',dz'$ に全く等しい）， $$\begin{aligned} ds^2 &= -\left(\sinh(\alpha ct')dx' + (\alpha x' + 1)\cosh (\alpha ct')d(ct')\right)^2 \\ & \quad \quad \quad +\left(\sinh(\alpha ct')dx' + (\alpha x' + 1)\cosh (\alpha ct')d(ct')\right)^2 + dy'^2 + dz'^2 \\ &= - \left(1 + \alpha x'\right)^2 d(ct')^2 + dx'^2 + dy'^2 + dz'^2 \end{aligned}$$ となります。よって，等加速度系における，計量テンソル $g'_{\mu\nu}$ について， $$g'_{\mu\nu} = \begin{cases} -\left(1 + \alpha x'\right)^2 & (\mu = \nu = 0)\\ 1 & (\mu = \nu \neq 0)\\ 0 & \text{(otherwise)} \end{cases}$$ とできます。

←前の記事　後の記事→