【解答・解説】京大物理2025 第1問 -力学-
2025年度の京大物理第1問を解説します。力学の単元です。
この記事に関連するQ&A
問題
問題
以下の問題は,2025年度京都大学入試問題物理第1問から引用しています(一部修正しています)。
なお,本記事中の図は全て,2025年度京都大学入試問題物理第1問を参考に,ライターが作成したものです(一部見やすさ等のためライターが変更した部分があります)。
次の文章を読んで, に適した式または数値を,{ }からは適切なものを一つ選びその番号を,それぞれの解答欄に記入せよ。また,問1では,指示にしたがって,解答を解答欄に記入せよ。ただし,円周率を ,重力加速度の大きさを とする。
(1)図1(a)のような自然長 で質量が無視できるばねの一端に,質量 で大きさが無視できる小球を取り付けた。
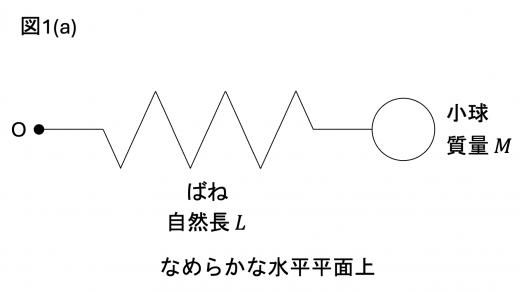
このばねのばね定数は である。一体となったばねと小球を,なめらかな水平平面上に置き,小球がついていない方のばねの端を,水平平面上の点 O に固定した。ばねは点 O のまわりを自由に回転できる。
水平平面上で,小球を点 O のまわりで,ある一定の角速度 で等速円運動させたとき,ばねは伸びて,図1(b)のように点 O から小球までの距離が であった。
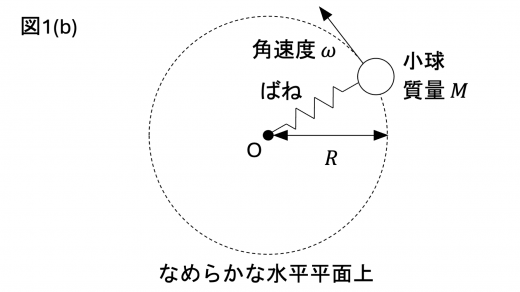
ばねの復元力により小球には点 O の方向へ大きさ の力がかかっている。また小球には点 O から遠ざかる方向へ大きさ の遠心力がかかっている。反対の方向へ働くこれらの力の大きさは,いずれも点 O から小球までの距離に依存する。すなわち,角速度が の場合に,両者の大きさが等しくなる点 O から小球までの距離が であり,それは を用いて と表される。
問1 図1(b)の小球が等速円運動を行うための条件を角速度 の範囲で示せ。
(2)図2(a)のように,質量が無視できる軽くて伸び縮みしない長さ のひもの一端を,なめらかな水平面上の点 O に固定した。また,このひものもう一方の端に,質量 で大きさが無視できる小球1を取り付けた。小球1にはさらに,質量が無視できる軽くて伸び縮みしない長さ のひもの一端を取り付け,そのひもの他端には質量 で大きさが無視できる小球2を取り付けた。
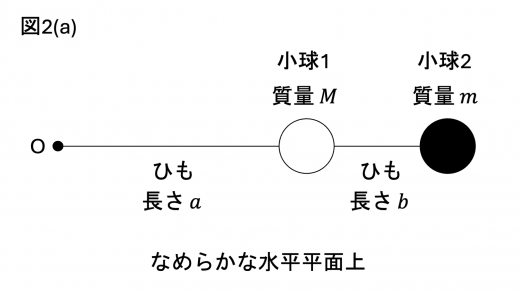
はじめ,2つの小球と2本のひもは,一直線上に連結されたまま,なめらかな水平面上で,点 O を中心とする角速度 の等速円運動をしていた。図2(b)中に示す通り,点 O を座標原点とし,水平平面上のある方向に 軸を,それと垂直な方向に 軸をとる。
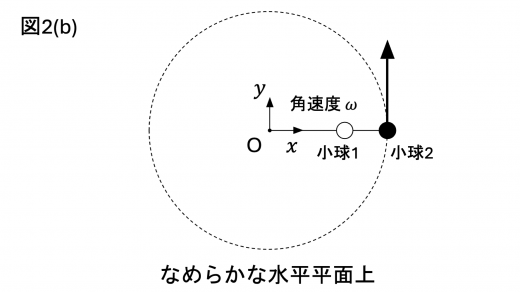
回転している小球2の座標が とする。なお切れた後のひもは,その後の2つの小球の運動には影響を与えないものとする。
長さ のひもで連結された2つの小球の運動に注目する。ひもが切れた直後の2つの小球の重心の位置は である。このとき重心から見た小球1の相対速度の大きさは であり,その向きは {キ:① 軸正の方向,② 軸負の方向,③ 軸正の方向,④ 軸負の方向} である。このとき重心から見た小球2の相対速度の大きさや向きも,小球1のそれらと同様に求めることができる。小球1と小球2を連結する長さ のひもにかかっている張力は であり,2つの小球は重心まわりを角速度 で回転する。また,重心の運動は2つの小球の質量が重心に集中したものであると考えることができる。重心にかかる加速度の大きさは であることから,重心は {サ:①円運動,②直線運動,③単振動} することがわかる。
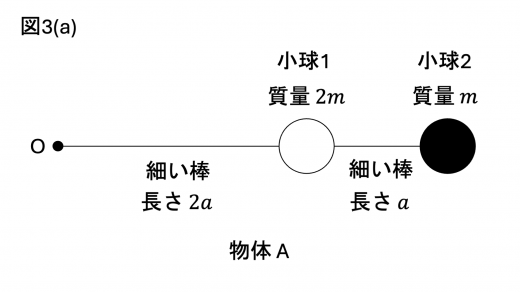
(3)図3(a)のような,質量が無視できる2本の変形しない細い棒と,大きさが無視できる2つの小球が連結された物体 A を作製した。まず長さ の細い棒の一端に質量 の小球1を接着した。小球1にはさらに,長さ の細い棒の一端を固定し,さらにその細い棒の他端には質量 の小球2を固定した。長さ の細い棒と長さ の細い棒は,それぞれの軸の延長線が完全に一致している。
水平な地面からある高さの位置に,地面に平行に設置されたまっすぐで細い鉄棒がある。さきに作製した物体Aを構成する細い棒の,いずれかの小球とも接続されていない一端を,この鉄棒に垂直に取り付けた。図3(b)は,物体 A を取り付けた点を含む鉄棒に垂直な平面を,鉄棒の軸方向から見た図である。
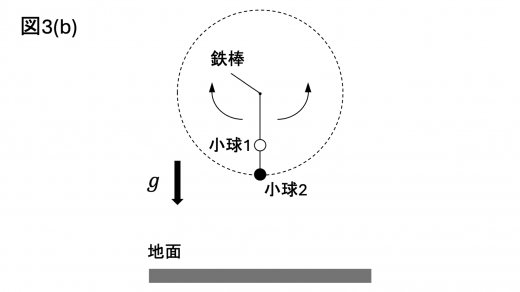
連結された物体 A は,鉄棒に垂直なこの平面内で,鉄棒に垂直なこの平面内で,鉄棒のまわりを自由に回転できる。
はじめ,物体 A が図4(a)のように地面と平行となるように保持されている。座標原点 O を鉄棒の位置にとり,そこから小球2の方向を 軸正の方向,鉛直上方を 軸正の方向とする。また図4(a)中に示す通り, 軸からの回転角を (反時計周りを正,単位はラジアン) で表す。ただし とし,たとえば 軸正の方向は で表される。
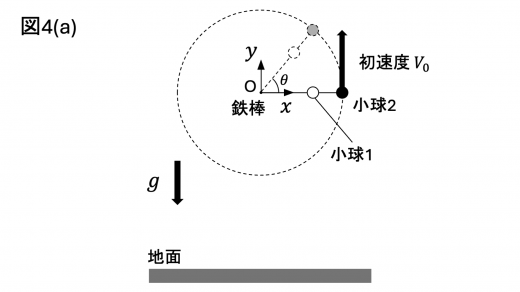
物体 A が の位置にあるとき,鉛直上方へ向かう初速度を小球2に与えた。小球2の初速度を とすると,このとき物体 A のもつ運動エネルギーは と書ける。また, を位置エネルギーの基準高さとすると,初速度を与えられたのち,物体 A が回転して回転角が となったときに,物体 A がもつ位置エネルギーは と書ける。
以下では として, を用いずに解答せよ。
物体 A が初めて の位置に到達する直前には,物体 A は図4(a)の方向から見たとき {セ:①時計回り,②反時計回り} に回転している。
物体 A が の位置に到達したとき,その回転の大きさは である。このとき,接着してあった長さ の細い棒と小球1の連結部が一瞬で外れた。連結が外れた瞬間の時刻を とする。長さ の細い棒で連結された2つの小球の, での運動を考える。 で初めて小球2が小球1の鉛直下方に到達したとき,ちょうど小球2が地面に接した(図4(b))。
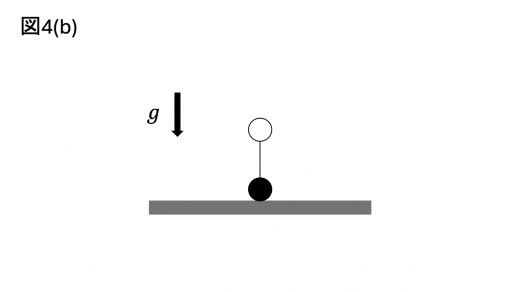
よって地面を基準として,鉄棒の高さは であると求められる。
相対運動と円運動に関する問題です。
解答例
解答例
(1)
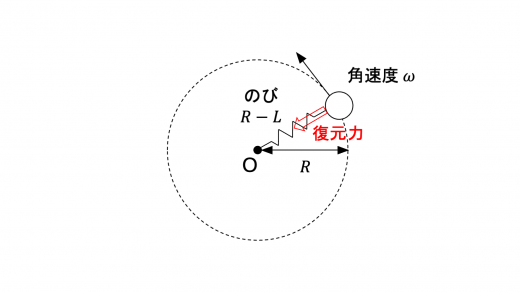
自然長が であること,また問題文より であることから,ばねの復元力 (単振動のまとめ) は,点 O の方向へ大きさ ア: であることがわかります。
小球は半径 ,角速度 の等速円運動 (円運動とは|円運動における加速度・向心力・遠心力) をしていることから,小球にはたらく遠心力の大きさは イ: と求められます。
小球とともに回転する系から見て力のつりあいより
に関するこの方程式が解を持つとして解くと
と求められます。
問1
この小球が等速円運動を行うためには,(1-1)式が正の解を持つ必要があります。これより の条件は
と求められます。
(2)
まず,ひもが切れた直後,小球1・2の座標はそれぞれ であることから,2つの小球の重心 G の座標 は
と求められます。
また,ひもが切れた直後の小球1・2の速度 は,それぞれ
であることから,ひもが切れた直後の重心 G の速度 は
したがって,ひもが切れた直後の,重心から見た小球1の相対速度 は
この大きさ は カ: となります。また, の向きを考えることにより,向きは キ:④ ( 軸負の向き) であることがわかります。
ここで,重心 G に加わる力は常につりあっている (力のつりあい・作用反作用との違い) ため,重心にかかる加速度の大きさは コ:0 であり,重心の運動は サ:② (直線運動) であることがわかります。
さて,重心系から小球1・2の運動を考えます。重心の加速度が0であることと,小球1・2に加わる力は張力のみで,張力は常に小球1・2の速度と直交する向きにはたらくことを考えると,エネルギー保存則により,重心系から見た小球1・2は重心 G を中心に等速円運動することがわかります。
このときの角速度を とします。重心 G から見た小球1の等速円運動の半径は であり,相対速度の大きさは常にカであることから,
求める張力を とすると,重心から見た小球1の運動方程式より
と求められます。
(3)
小球1・2は一体となって運動することより,これらは同じ角速度で運動します。角速度が等しい円運動の速度はその半径に比例するので,小球1の初速度 は,小球2の初速度ベクトルを とすると
大きさ は であることがわかります。
したがって,物体 A の運動エネルギー は
と求められます。
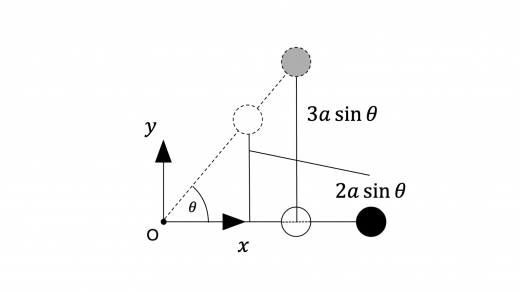
また, を位置エネルギーの基準高さとすると,上図から,物体 A がもつ位置エネルギー (位置エネルギーの定義と例(重力・弾性力・クーロン力)) は
となります。
物体 A が初めて に到達したときの物体 A の運動の方向を考えます。
そのためには,物体 A が (円運動が到達できる最高到達点) に到達したとき,位置エネルギー が を下回るかどうかを調べればよいことがわかります。もし下回るなら,エネルギー保存則 (運動量保存則とエネルギー保存則の導出) より物体 A はその地点で正の速さを持ち,最高到達点に達してもそのまま反時計回りに運動を続けます。もし上回るなら, でエネルギー保存則は成り立たず,したがってそれ以前の角度で物体 A の運動は静止します。その後物体 A は折り返して時計回りに運動します。
(ス)の結果より
一方 であることより
したがって,上記の議論より,物体 A が初めて に到達したときの物体 A の運動の方向は セ:② (反時計回り) であることがわかります。
回転の角速度を求めるために,まず での小球2の速度 を求めます。これはエネルギー保存則より
円運動の速さと角速度の関係より,求める角速度 は
となります。
この瞬間長さ の細い棒と小球1の連結部が一瞬で外れることを考えます。このときを とします。
重心 G’ は重力加速度 により, 軸方向に等加速度運動を行います。また,重心 G’ から見た小球1・2の運動は,重力分が打ち消されるために (詳しくは 慣性系と非慣性系の定義|相対性原理と物理法則),上記の議論と同様に,角速度 で等速円運動を行います。
で初めて小球2が小球1の鉛直下方に到達するのは,この等速円運動がちょうど1周期だけ経過したときで,このときの時刻 は
となります。
地面の高さを ,鉄棒の高さを とします。 での重心 G’ の 座標 は
その後,G’ は で
このとき小球2は重心の鉛直下方にあり,さらに地面に接するので,鉄棒の高さ は
のように求めることができます。
2物体系の運動を,重心とその相対運動に分解して捉えるのは,入試の力学の問題では比較的よくあるパターンです。一度はやっておいて損はありません。











