1量子ビットゲート
1量子ビットゲート(1量子ゲート)は,量子コンピュータ・量子計算を扱う上で何度も登場する重要な概念です。
各種の1量子ビットゲートについて,数式を用いて解説していきます。
量子回路の読み方
量子回路の読み方
量子回路について,詳細は別記事にて解説予定ですので,この記事では詳細は説明しません。この記事の1量子ビットゲートの解説のために必要な部分について触れます。
いま,量子状態 に,ユニタリ行列で表される操作 を行ったとき,量子状態が に変化したとします。
この操作を表す量子回路は例えば以下のように書きます。
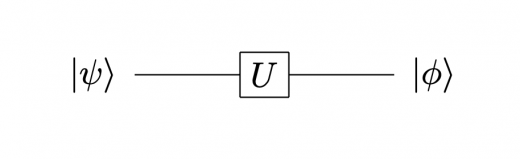
量子回路図では,時間は左から右に進みます。また,図の最も左側の状態が入力,最も右側の状態が出力となっています。
別の例についても量子回路を書いてみます。いま,量子状態 に,ユニタリ行列で表される操作 をこの順で行ったとき,量子状態が に変化したとします。これは数式では以下のように表すことができます。
この操作を表す量子回路は例えば以下のように書きます。
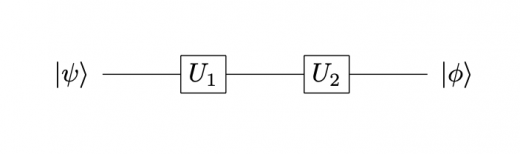
量子回路図では左から の順で並びますが,数式上では左から の順で並ぶことに注意してください。
パウリゲート
パウリゲート
パウリゲートとは,Xゲート,Yゲート,Zゲートの3つの総称です。
Xゲート
Xゲートとは,以下のように表される行列です。
Xゲートは,計算基底 に以下のように作用します。
このように,Xゲートはビットあるいはスピンをフリップさせるという役割を持っています。量子ビットにおいて0を1,1を0に変換しているという観点から,古典コンピュータにおけるNOT演算子としてはたらいているとも考えることができます。
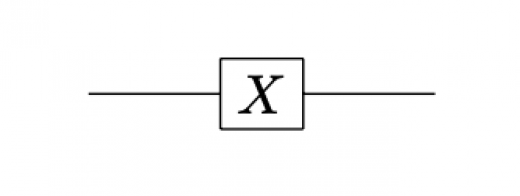
量子回路では,Xゲートは以下のように表されます。
Yゲート
Yゲートとは,以下のように表される行列です。
Yゲートは,計算基底 に以下のように作用します。
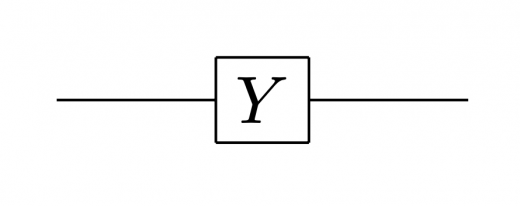
量子回路では,Yゲートは以下のように表されます。
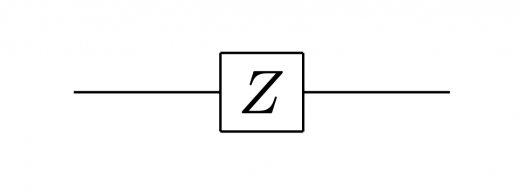
Zゲート
Zゲートとは,以下のように表される行列です。
Zゲートは,計算基底 に以下のように作用します。
これより,Zゲートは には何もしないが, は位相を反転させるという役割があります。
また,Zゲートは および を固有ベクトルに持つということもわかります。
Zゲートが および を固有ベクトルに持つということを,線形代数の知識から確認しておきます。
固有方程式 を解くことを考えます。
に対応する固有ベクトル を求めます。
規格化を考えて, と求められます。したがって, です。
次に, に対応する固有ベクトル を求めます。
規格化を考えて, と求められます。したがって, です。
量子回路では,Zゲートは以下のように表されます。
パウリゲートと単位行列
これらのパウリゲートは,2乗すると単位行列 になります。すなわち
これは簡単な計算によって確かめられます。ぜひ練習問題としてやってみてください。
アダマールゲート
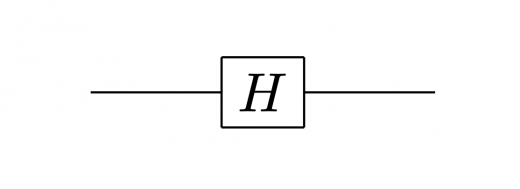
アダマールゲート
アダマールゲートは,以下のように表される行列です。
アダマールゲートは,計算基底 に以下のように作用します。
状態 については,量子ビットとブロッホ球 も併せてご覧ください。
アダマールゲートの特徴は, に作用させると, に戻るという点です。
量子回路では,アダマールゲートは例えば以下のように表されます。
アダマールゲートと単位行列
アダマールゲートも,パウリゲート同様,2乗すると単位行列 になります。
これも簡単な計算により確かめられますので,ぜひ手を動かしてみてください。
この記事に関連するQ&A
Sゲート,Tゲート
Sゲート,Tゲート
Sゲート,Tゲートのはたらき
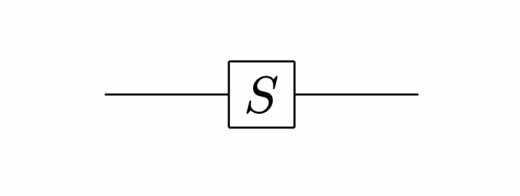
Sゲート,Tゲートはそれぞれ以下のように表される行列です。
SゲートとTゲートは,ブロッホ球上での位相の回転に対応しています。Sゲートは位相を ,Tゲートは位相を だけ回転させることができます。これを計算により確かめてみましょう。
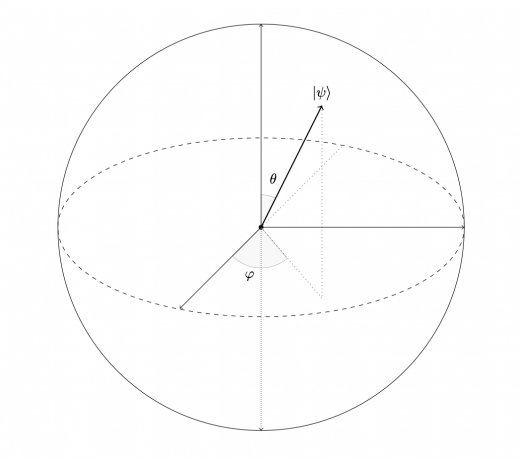
いま,ブロッホ球上の任意の量子状態 は,2つの角度 を用いて以下のように表すことができるのでした。(量子ビットとブロッホ球 も併せてご覧ください。)
この量子状態に,SゲートとTゲートをそれぞれ作用させてみましょう。 に注意して
よって,Sゲートは位相を ,Tゲートは位相を だけ回転させることが確かめられました。
Sゲート,Tゲートは,量子回路では例えば下図のように表すことができます。
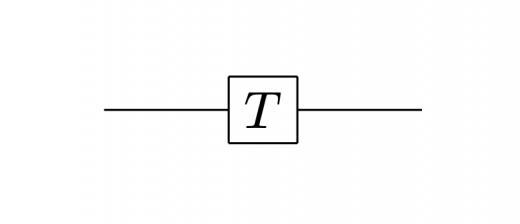
Sゲート,Tゲートと他のゲートとの対応
以下の数式が成り立つことが,簡単な計算により確かめることができます。
この関係式からも,Zゲートがブロッホ球上で 回転に対応していることがわかります。
位相ゲート
ブロッホ球上で任意の角度 だけ回転させる位相ゲート を考えることができます。Sゲート,Tゲートの計算により, は以下のように表されることがわかります。
回転ゲート
回転ゲート
ブロッホ球上の を通っている軸を 軸としたときの, 軸それぞれの周りで原点周りに 回転させるゲート を考えることができます。これは,それぞれ以下のように表すことができます。
ここでは, の中辺 = 右辺となることを確かめます。簡単のため, とおきます。
ここで, となることを考えると,
と整理できます。いま,
とおきます。 より,それぞれ
ここでは, のテイラー変換の知識を使いました。
したがって
同様の計算により
であることも確かめられます。
のテイラー展開については,基本的なテイラー展開・マクローリン展開公式一覧) なども併せてご覧ください。
【補足】1量子ビットゲートとユニタリ性
【補足】1量子ビットゲートとユニタリ性
ここまでいくつか1量子ビットゲートを紹介してきました。これらは全てユニタリ行列になっているという特徴があります。
ユニタリ行列については
も併せてご覧ください。
各1量子ビットゲートがユニタリ行列になっているというのは,簡単な計算により確かめられるので,ぜひやってみてください。
量子コンピュータ「らしい」話になってきたのではないでしょうか。











