2量子ビットゲート

更新 2025/01/09

量子コンピュータ・量子情報の分野で登場する量子ビットゲートのうち，2つの量子ビットに作用する2量子ビットゲートとは何か，解説します。特に，CNOTゲート，CXゲート，SWAPゲートについて解説します。

【準備】2量子ビットの量子回路の書き方

1量子ビットゲートの記事 (今後公開予定です) において，1量子ビットの場合の量子回路の書き方について軽くご紹介しました。ここでは，入力と出力が2量子ビットの場合の量子回路の書き方について軽く触れておきましょう。
例えば，入力として ∣ψϕ⟩=∣ψ⟩⊗∣ψ⟩| \psi \phi \rangle = | \psi \rangle \otimes | \psi \rangle∣ψϕ⟩=∣ψ⟩⊗∣ψ⟩ という状態を考えます。
量子ビットが複数個ある場合のナンバリングの仕方は，文献ごとでも異なります。この記事ではケットで書いた場合の左側から1番目，2番目，…と数えることにします。上の入力の状態の例で言うと，1番目の量子ビットは ∣ψ⟩| \psi \rangle∣ψ⟩，2番目の量子ビットは ∣ϕ⟩| \phi \rangle∣ϕ⟩ となります。
この量子状態に以下のように操作を施すことを考えます。
∣ψ′ϕ′⟩=U∣ψϕ⟩
| \psi' \phi' \rangle = U | \psi \phi \rangle
∣ψ′ϕ′⟩=U∣ψϕ⟩
UUU は2量子ビットに作用する量子ゲートとします。
これは量子回路では，例えば下図のように書くことができます。
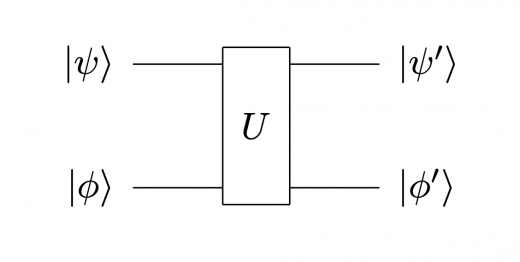
この記事では，量子回路の入出力状態について，上から1番目，2番目…と量子ビットを書くことにします。
また，同じ量子状態 ∣ψϕ⟩| \psi \phi \rangle∣ψϕ⟩ を入力状態として用意し，∣ψ⟩| \psi \rangle∣ψ⟩ には U1U_1U1​ を，∣ϕ⟩| \phi \rangle∣ϕ⟩ には U2U_2U2​ を作用させることを考えてみます。
これは数式では下図のように表すことができます。
∣ψ′′ϕ′′⟩=U1∣ψ⟩⊗U2∣ϕ⟩
| \psi'' \phi'' \rangle = U_1 | \psi \rangle \otimes U_2| \phi \rangle
∣ψ′′ϕ′′⟩=U1​∣ψ⟩⊗U2​∣ϕ⟩
これは量子回路では，例えば下図のように表すことができます。

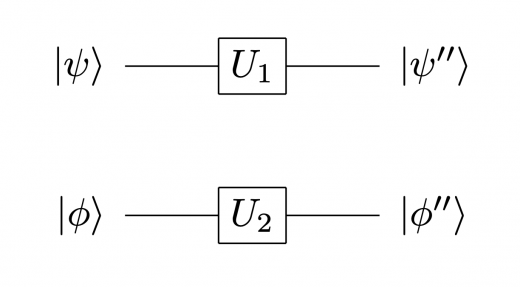
【準備】2量子ビットの計算基底

2量子ビットの計算基底として，∣00⟩,∣01⟩,∣10⟩,∣11⟩| 00 \rangle, | 01 \rangle, | 10 \rangle, | 11\rangle∣00⟩,∣01⟩,∣10⟩,∣11⟩ の4つの量子状態を用意することが多いです。
これらは，ベクトル表示では以下のような計算基底に対応しています。
∣00⟩=(1000),∣01⟩=(0100),∣10⟩=(0010),∣11⟩=(0001)
| 00 \rangle = 
\begin{pmatrix}
1 \\
0 \\
0 \\
0
\end{pmatrix}, 
| 01 \rangle = 
\begin{pmatrix}
0 \\
1 \\
0 \\
0
\end{pmatrix}, 
| 10 \rangle = 
\begin{pmatrix}
0 \\
0 \\
1 \\
0
\end{pmatrix}, 
| 11 \rangle = 
\begin{pmatrix}
0 \\
0 \\
0 \\
1
\end{pmatrix}
∣00⟩=⎝⎛​1000​⎠⎞​,∣01⟩=⎝⎛​0100​⎠⎞​,∣10⟩=⎝⎛​0010​⎠⎞​,∣11⟩=⎝⎛​0001​⎠⎞​

CNOTゲート

CNOT ゲートとは，2量子ビットのうち片方が1であった場合，もう片方のビットをフリップさせる操作を行うゲートのことです。1であるかどうかを判断する量子ビットを制御ビット，フリップさせる量子ビットを標的ビットなどと呼びます。以下では，特に断りがない場合，1番目の量子ビットを制御ビット，2番目の量子ビットを標的ビットとした場合の CNOT ゲートを考えます。
CNOT ゲートは，量子回路の図では下図のように表すことができます。
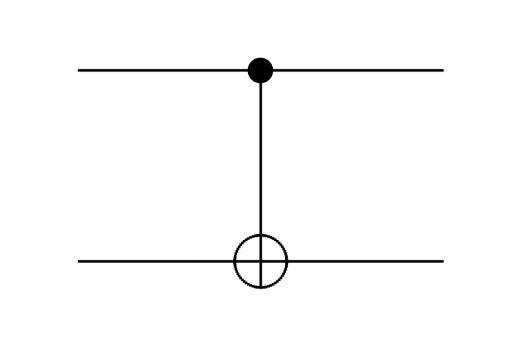
下図のようにも表すことができます。
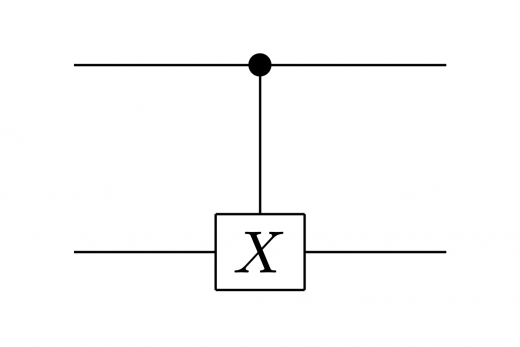
CNOT ゲートの行列表示CNOT ゲートの行列表示を考えてみましょう。2量子ビットの1状態は4次元複素ベクトルで表されるので，CNOT ゲートは4行4列のユニタリ行列となることが予想されます。
線形代数では，ある行列の行列表示が知りたい場合，その行列を基底に作用させた結果がわかればよいという事実がありました。以下の記事なども併せてご参照ください。
基底の変換行列～定義と具体例
CNOT ゲートを ∣00⟩,∣01⟩,∣10⟩,∣11⟩| 00 \rangle, | 01 \rangle, | 10 \rangle, | 11\rangle∣00⟩,∣01⟩,∣10⟩,∣11⟩ に作用させた場合の結果を考えてみましょう。量子状態としての表記では，左から順に1番目，2番目と量子ビットを数えていたことに注意すると，これら4つの量子状態への作用は以下のように書けます。
CNOT∣00⟩=∣00⟩=(1000)
\text{CNOT} | 00 \rangle = | 00 \rangle = 
\begin{pmatrix}
1 \\
0 \\
0 \\
0
\end{pmatrix}
CNOT∣00⟩=∣00⟩=⎝⎛​1000​⎠⎞​
CNOT∣01⟩=∣01⟩=(0100)
\text{CNOT} | 01 \rangle = | 01 \rangle = 
\begin{pmatrix}
0 \\
1 \\
0 \\
0
\end{pmatrix}
CNOT∣01⟩=∣01⟩=⎝⎛​0100​⎠⎞​
CNOT∣10⟩=∣11⟩=(0001)
\text{CNOT} | 10 \rangle = | 11 \rangle = 
\begin{pmatrix}
0 \\
0 \\
0 \\
1
\end{pmatrix}
CNOT∣10⟩=∣11⟩=⎝⎛​0001​⎠⎞​
CNOT∣11⟩=∣10⟩=(0010)
\text{CNOT} | 11 \rangle = | 10 \rangle = 
\begin{pmatrix}
0 \\
0 \\
1 \\
0
\end{pmatrix}
CNOT∣11⟩=∣10⟩=⎝⎛​0010​⎠⎞​
したがって，CNOT ゲートを行列表示すると，以下のようになることがわかります。
CNOT=(1000010000010010)
\text{CNOT} = 
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{pmatrix}
CNOT=⎝⎛​1000​0100​0001​0010​⎠⎞​

どの古文単語帳を使おうか悩んでいます…おすすめの古文単語帳を教えていただきたいです！ 2

高校化学で、以下の問題がわからないので教えていただきたいです！ある温度で、2.0Lの容器に水素0.50 molとヨウ素 3

「物理のエッセンス」「良問の風」「名問の森」「物理授業の実況中継」の4冊の参考書を難易度順に並び替えてください！それぞ 4

スタディサプリで高校数学を独学していますが、平日は授業動画を毎日見る時間があまり取れません。土日にまとめて学習することが 5

CZゲート

CZ ゲートとは，2量子ビットのうち片方が1であった場合，もう片方の量子ビットに Z ゲートを作用させるような操作を行うゲートのことです。以下では、特に断りがない場合，1番目の量子ビットを制御ビット，2番目の量子ビットを標的ビットとした場合について考えます。
CZ ゲートは，量子回路では以下のように表すことができます。
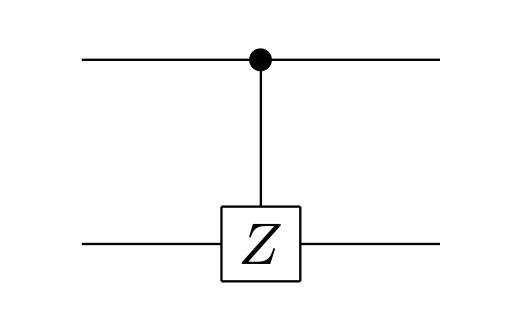
CZ ゲートの行列表示Zゲートは0の量子ビットには何もしないが，1の量子ビットは符号を反転させるという効果がありました (別記事にて解説予定です)。したがって，CZ ゲートは，2量子ビットの計算基底に以下のように作用することがわかります。
CZ∣00⟩=∣00⟩=(1000)
\text{CZ} | 00 \rangle = | 00 \rangle = 
\begin{pmatrix}
1 \\
0 \\
0 \\
0
\end{pmatrix}
CZ∣00⟩=∣00⟩=⎝⎛​1000​⎠⎞​
CZ∣01⟩=∣01⟩=(0100)
\text{CZ} | 01 \rangle = | 01 \rangle = 
\begin{pmatrix}
0 \\
1 \\
0 \\
0
\end{pmatrix}
CZ∣01⟩=∣01⟩=⎝⎛​0100​⎠⎞​
CZ∣10⟩=∣10⟩=(0010)
\text{CZ} | 10 \rangle = | 10 \rangle = 
\begin{pmatrix}
0 \\
0 \\
1 \\
0
\end{pmatrix}
CZ∣10⟩=∣10⟩=⎝⎛​0010​⎠⎞​
CZ∣11⟩=−∣11⟩=(000−1)
\text{CZ} | 11 \rangle = - | 11 \rangle = 
\begin{pmatrix}
0 \\
0 \\
0 \\
-1
\end{pmatrix}
CZ∣11⟩=−∣11⟩=⎝⎛​000−1​⎠⎞​
したがって，CZ ゲートを行列表示すると，以下のようになることがわかります。
CNOT=(100001000010000−1)
\text{CNOT} = 
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & -1
\end{pmatrix}
CNOT=⎝⎛​1000​0100​0010​000−1​⎠⎞​

SWAPゲート

SWAP ゲートとは，作用する2つの量子ビットの状態を入れ替えるようなゲートのことです。
SWAP∣ψϕ⟩=∣ϕψ⟩
\text{SWAP} | \psi \phi \rangle = |\phi \psi \rangle
SWAP∣ψϕ⟩=∣ϕψ⟩
SWAP ゲートは，量子回路では以下のように表すことができます。
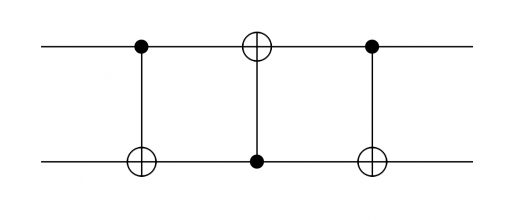
上図からわかるように，SWAP ゲートは CNOT ゲートを3回作用させたものとなっています。
SWAP ゲートの行列表示これまで同様，4つの計算基底への作用がどうなるか確認してみましょう。
SWAP∣00⟩=∣00⟩=(1000)
\text{SWAP} | 00 \rangle = | 00 \rangle = 
\begin{pmatrix}
1 \\
0 \\
0 \\
0
\end{pmatrix}
SWAP∣00⟩=∣00⟩=⎝⎛​1000​⎠⎞​
SWAP∣01⟩=∣10⟩=(0010)
\text{SWAP} | 01 \rangle = | 10 \rangle = 
\begin{pmatrix}
0 \\
0 \\
1 \\
0
\end{pmatrix}
SWAP∣01⟩=∣10⟩=⎝⎛​0010​⎠⎞​
SWAP∣10⟩=∣01⟩=(0100)
\text{SWAP} | 10 \rangle = | 01 \rangle = 
\begin{pmatrix}
0 \\
1 \\
0 \\
0
\end{pmatrix}
SWAP∣10⟩=∣01⟩=⎝⎛​0100​⎠⎞​
SWAP∣11⟩=∣11⟩=(0001)
\text{SWAP} | 11 \rangle = | 11 \rangle = 
\begin{pmatrix}
0 \\
0 \\
0 \\
1
\end{pmatrix}
SWAP∣11⟩=∣11⟩=⎝⎛​0001​⎠⎞​
したがって，SWAP ゲートを行列表示すると，以下のようになることがわかります。
SWAP=(1000001001000001)
\text{SWAP} = 
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
SWAP=⎝⎛​1000​0010​0100​0001​⎠⎞​
【発展】SWAP ゲートの表式の確認SWAP ゲートが上の表式で正しいことを，任意の場合で確認してみましょう。なお，以下ではベクトルのテンソル積の知識を用いています。
∣ψ⟩=(a1a2),∣ϕ⟩=(b1b2)
| \psi \rangle = 
\begin{pmatrix}
a_1 \\
a_2
\end{pmatrix}, 
| \phi \rangle = 
\begin{pmatrix}
b_1 \\
b_2
\end{pmatrix}
∣ψ⟩=(a1​a2​​),∣ϕ⟩=(b1​b2​​)
とします。このとき，2量子状態 ∣ψϕ⟩| \psi \phi \rangle∣ψϕ⟩ は
∣ψϕ⟩=∣ψ⟩⊗∣ϕ⟩=(a1b1a1b2a2b1a2b2)=a1b1∣00⟩+a1b2∣01⟩+a2b1∣10⟩+a2b2∣00⟩
\begin{aligned}
| \psi \phi \rangle &= | \psi \rangle \otimes | \phi \rangle \\
&= 
\begin{pmatrix}
a_1 b_1 \\
a_1 b_2 \\
a_2 b_1 \\
a_2 b_2
\end{pmatrix} \\
&= a_1 b_1 | 00 \rangle + a_1 b_2 | 01 \rangle + a_2 b_1 | 10 \rangle + a_2 b_2 | 00 \rangle
\end{aligned}
∣ψϕ⟩​=∣ψ⟩⊗∣ϕ⟩=⎝⎛​a1​b1​a1​b2​a2​b1​a2​b2​​⎠⎞​=a1​b1​∣00⟩+a1​b2​∣01⟩+a2​b1​∣10⟩+a2​b2​∣00⟩​
のように表されます。したがって
SWAP∣ψϕ⟩=a1b1∣00⟩+a1b2∣10⟩+a2b1∣01⟩+a2b2∣00⟩=(a1b1a2b1a1b2a2b2)
\begin{aligned}
\text{SWAP} | \psi \phi \rangle &= a_1 b_1 | 00 \rangle + a_1 b_2 | 10 \rangle + a_2 b_1 | 01 \rangle + a_2 b_2 | 00 \rangle \\
&= 
\begin{pmatrix}
a_1 b_1 \\
a_2 b_1 \\
a_1 b_2 \\
a_2 b_2
\end{pmatrix}
\end{aligned}
SWAP∣ψϕ⟩​=a1​b1​∣00⟩+a1​b2​∣10⟩+a2​b1​∣01⟩+a2​b2​∣00⟩=⎝⎛​a1​b1​a2​b1​a1​b2​a2​b2​​⎠⎞​​
となります。一方，∣ϕψ⟩| \phi \psi \rangle∣ϕψ⟩ は
∣ϕψ⟩=∣ϕ⟩⊗∣ψ⟩=(b1a1b1a2b2a1b2a2)
\begin{aligned}
| \phi \psi \rangle &= | \phi \rangle \otimes | \psi \rangle \\
&= 
\begin{pmatrix}
b_1 a_1 \\
b_1 a_2 \\
b_2 a_1 \\
b_2 a_2
\end{pmatrix}
\end{aligned}
∣ϕψ⟩​=∣ϕ⟩⊗∣ψ⟩=⎝⎛​b1​a1​b1​a2​b2​a1​b2​a2​​⎠⎞​​
のように表されます。したがって，任意の2量子状態について
SWAP∣ψϕ⟩=∣ϕψ⟩
\text{SWAP} | \psi \phi \rangle = | \phi \psi \rangle
SWAP∣ψϕ⟩=∣ϕψ⟩
が成り立ちます。
SWAP ゲートと CNOT ゲートとの対応制御ビットを iii 番目の量子ビット，標的ビットを jjj 番目の量子ビットとした場合の CNOT ゲートを CNOTij\text{CNOT}_{ij}CNOTij​ と書くことにします。
このとき，量子回路図からもわかるように，SWAP ゲートと CNOT ゲートの間には，
SWAP=CNOT12⋅CNOT21⋅CNOT12
\text{SWAP} = \text{CNOT}_{12} \cdot \text{CNOT}_{21} \cdot \text{CNOT}_{12}
SWAP=CNOT12​⋅CNOT21​⋅CNOT12​
という関係があります。
計算による確認計算により確かめてみましょう。まず，CNOT21\text{CNOT}_{21}CNOT21​　の行rつ表記について求めます。
CNOT21∣00⟩=∣00⟩
\text{CNOT}_{21} |00 \rangle = |00 \rangle
CNOT21​∣00⟩=∣00⟩
CNOT21∣01⟩=∣11⟩
\text{CNOT}_{21} |01 \rangle = |11 \rangle
CNOT21​∣01⟩=∣11⟩
CNOT21∣10⟩=∣10⟩
\text{CNOT}_{21} |10 \rangle = |10 \rangle
CNOT21​∣10⟩=∣10⟩
CNOT21∣11⟩=∣01⟩
\text{CNOT}_{21} |11 \rangle = |01 \rangle
CNOT21​∣11⟩=∣01⟩
より，
CNOT21=(1000000100100100)
\text{CNOT}_{21} = 
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0
\end{pmatrix}
CNOT21​=⎝⎛​1000​0001​0010​0100​⎠⎞​
と表すことができます。
CNOT12⋅CNOT21⋅CNOT12=CNOT12⋅(1000000100100100)⋅(1000010000010010)=(1000010000010010)⋅(1000001000010100)=(1000001001000001)=SWAP
\begin{aligned}
\text{CNOT}_{12} \cdot \text{CNOT}_{21} \cdot \text{CNOT}_{12} &= \text{CNOT}_{12} \\
& \cdot 
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0
\end{pmatrix} \cdot 
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{pmatrix} \\
&= 
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{pmatrix} \cdot
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
0 & 1 & 0 & 0
\end{pmatrix} \\
&= 
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix} \\
& = \text{SWAP}
\end{aligned}
CNOT12​⋅CNOT21​⋅CNOT12​​=CNOT12​⋅⎝⎛​1000​0001​0010​0100​⎠⎞​⋅⎝⎛​1000​0100​0001​0010​⎠⎞​=⎝⎛​1000​0100​0001​0010​⎠⎞​⋅⎝⎛​1000​0001​0100​0010​⎠⎞​=⎝⎛​1000​0010​0100​0001​⎠⎞​=SWAP​

【補足】2量子ビットゲートとユニタリ性

1量子ビットゲートは全てユニタリ行列であるという性質があります。この記事で紹介した2量子ビットゲートも，全てユニタリ行列となっていることが確認できます。ぜひ，練習問題としてやってみてください。

ユニタリ行列については

ユニタリ行列の定義と性質の証明

なども併せてご参照ください。

制御ビットと標的ビットは，計算や図と対応づけて覚えるのがやや難しいので，注意が必要です。