量子ビットとブロッホ球

量子ビット にて，量子ビットの状態は複素ベクトルで表すことができるということを説明しました。例えば，$| 0 \rangle$ と $| 1 \rangle$ が重なり合った1ビット量子状態 $| \psi \rangle$ は

$$\begin{aligned} | \psi \rangle &= \alpha | 0 \rangle + \beta | 1 \rangle \\ &= \alpha \begin{pmatrix} 1 \\ 0 \end{pmatrix} + \beta \begin{pmatrix} 0 \\ 1 \end{pmatrix} \\ &= \begin{pmatrix} \alpha \\ \beta \end{pmatrix} \end{aligned}$$

のように表すことができるのでした。この状態ベクトル $| \psi \rangle$ の大きさは，ベクトルの内積を考えると $\sqrt{| \alpha |^2 + | \beta |^2}$ のように表現することができます。

いま，状態ベクトル $| \psi \rangle$ の大きさが1であると考えましょう。量子力学では，状態ベクトルが定数倍であっても物理的には同じものとみなすため，こうしても一般性を失いません。そうすると，実数 $\theta \in [0, 2 \pi )$ を用いて

$$| \alpha | = \cos{\theta}, | \beta | = \sin{\theta}$$

と表すことができます。

さらに，$\alpha, \beta$ は複素数なので，大きさ1の位相因子ぶんの自由度があります。すなわち

$$\alpha = e^{i \phi_\alpha } \cos{\theta}, \beta = e^{i \phi_\beta } \sin{\theta}$$

のように表現することができます。

さて，この表現をはじめの式に代入すると

$$\begin{aligned} | \psi \rangle &= e^{i \phi_\alpha} \cos{\theta} | 0 \rangle + e^{i \phi_\beta} \sin{\theta} | 1 \rangle \\ &= e^{i \phi_\alpha} (\cos{\theta} | 0 \rangle + e^{i \phi_\beta - \phi_\alpha} \sin{\theta} | 1 \rangle) \end{aligned}$$

$\phi_\alpha = \lambda, \phi_\beta - \phi_\alpha = \varphi$ と置き直します。さらに，天下り的に $\theta \to \theta/2$ とします。すると

$$| \psi \rangle = e^{i \lambda} \left( \cos{\dfrac{\theta}{2}} | 0 \rangle + e^{i \varphi} \sin{\dfrac{\theta}{2}} | 1 \rangle \right)$$

$\lambda$ はグローバル位相と呼ばれることもあります。このグローバル位相ぶんの違いは量子状態としては無視できるので，結局 $| \psi \rangle$ は

$$| \psi \rangle = \cos{\dfrac{\theta}{2}} | 0 \rangle + e^{i \varphi} \sin{\dfrac{\theta}{2}} | 1 \rangle \tag{☆}$$

$$\text{with} \, 0 \leq \theta < 2 \pi , \, 0 \leq \varphi < 2 \pi$$

のように表せます。

3次元の球面上の点は，その極座標表示を考えると，角度を2つ指定すれば一つに指定できることを考えると，この量子状態に対応する点を3次元球上の1点にマップすることが可能になります。このときの3次元球をブロッホ球と呼びます。

例えば，上の状態 $| \psi \rangle$ は，ブロッホ球上で以下のように表されます。

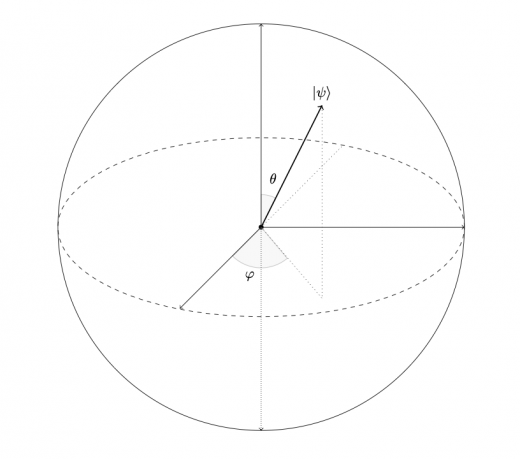
3次元極座標については，三次元極座標についての基本的な知識 についても併せてご覧ください。

いくつかの量子状態を例に取り，それらがブロッホ球のどこにあるか確かめてみましょう。

$| 0 \rangle$ と $| 1 \rangle$

まず，$| 0 \rangle$ がどこにあるかを考えてみます。(☆)式より

$$\cos{\dfrac{\theta}{2}} = 1, e^{i \varphi} \sin{\dfrac{\theta}{2}} = 0$$

$$\therefore \theta = 0$$

$\theta = 0$ は，Bloch 球上の北極に対応する点です。(逆に，そうなるように $\theta$ と $\varphi$ の取り方を定めたとも言えます。)$\varphi$ ぶんの自由度は上の連立方程式からは定まりませんが，対応する点は1つに定まっています。

同様に，$| 1 \rangle$ については

$$\cos{\dfrac{\theta}{2}} = 0, e^{i \varphi} \sin{\dfrac{\theta}{2}} = 1$$

$$\theta = \pi, \varphi = 0$$

これは，Bloch 球上の南極に対応する点になっています。

$| + \rangle$ と $| - \rangle$

$| + \rangle$ と $| - \rangle$ は，以下のように定義される状態です。

$$| + \rangle = \dfrac{| 0 \rangle + | 1 \rangle}{\sqrt{2}}$$

$$| - \rangle = \dfrac{| 0 \rangle - | 1 \rangle}{\sqrt{2}}$$

1量子ビットが取りうる量子状態として，何度も目にする重要な状態です。これらの状態のBloch球上の位置を求めてみます。

まず，$| + \rangle$ について

$$\cos{\dfrac{\theta}{2}} = \dfrac{1}{\sqrt{2}}, \, e^{i \varphi} \sin{\dfrac{\theta}{2}} = \dfrac{1}{\sqrt{2}}$$

$$\therefore \theta = \dfrac{\pi}{2}, \, \varphi = 0$$

また，$| - \rangle$ について

$$\cos{\dfrac{\theta}{2}} = \dfrac{1}{\sqrt{2}}, \, e^{i \varphi} \sin{\dfrac{\theta}{2}} = - \dfrac{1}{\sqrt{2}}$$

$$\therefore \theta = \dfrac{\pi}{2}, \, \varphi = \pi$$

$| 0 \rangle, | 1 \rangle, | + \rangle, | - \rangle$ をBloch球上に図示すると下図のようになります。

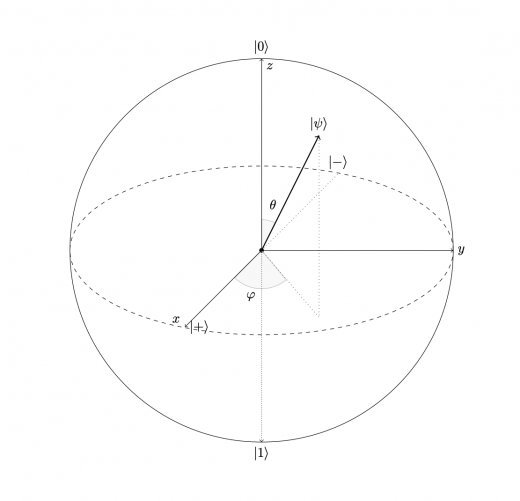
例えば，$| 0 \rangle, | 1 \rangle$ が $z$ 軸上の状態だとすると，$| + \rangle, | - \rangle$ は $x$ 軸上の状態となっています。

ブロッホ球には長所と短所があります。具体的にいくつか紹介します。

ブロッホ球の長所

• 1量子ビットの状態に対して図形的・視覚的に理解ができる
• 量子ゲートの操作がわかりやすい(量子ゲートについては別記事にて解説予定です)

ブロッホ球の短所

• 2量子ビット以上の量子状態を表すことができない