電池の内部抵抗
電池の内部抵抗について解説します。また,例題を用いて問題中での電池の内部抵抗の扱いを確認します。
この記事に関連するQ&A
電池の内部抵抗とは
電池の内部抵抗とは
起電力と端子電圧の関係
電池は,+極側の負電荷をー極側に流す装置です。負電荷をどれだけ運べるかという力を表す指標が「起電力」と呼ばれ,単位 [V] で表されます。
一方,回路内での電池の+極とー極の電位の差を「端子電圧」と呼びます。
理想的な状況であれば,起電力と端子電圧とは等しくなることが予想されます。ところが,回路に電流が流れている状況では,実際の端子電圧は起電力より小さくなることが観察されます。
この現象は,後述するように,電池の起電力の由来に関係しています。回路の問題としてこの現象を考えると,電池がその中に抵抗を持っていると考えることで説明できます。この仮想的な抵抗を「電池の内部抵抗」と呼びます。
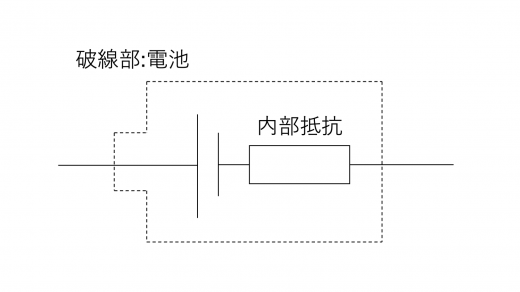
公式の求め方
以下のように,内部抵抗 を持つ起電力 の電池を用いて回路を構成したとき,回路に電流 が流れていると考えます。
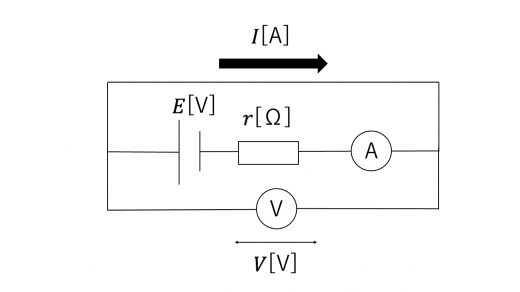
このとき,電池の電圧 は
として求められます。
この公式は,回路にキルヒホッフ第2法則を用いることで求めることができます。
(補足)上図の回路では,電圧計に電流は流れません。それは,電流計は非常に大きな抵抗を持っていると考えられるためです。(詳細は別記事にて解説予定です)
【補足】化学的観点からの考察
電池の起電力は,電池内部での化学反応により生じています。 電池は,この化学反応による化学エネルギーにより電子を輸送して,電流を発生させていると考えることができます。
電池内の化学反応できる物質はもちろん有限なので,反応を続け,電流を流し続けていくと,電池内部の物質の総量が減少し,電池内で生じる化学エネルギーもまた減少していきます。
このようにして電池の起電力は,電流を流していくうちに減少していくわけです。これを回路の問題として考えると,さも電池が内部抵抗を持っており,流れる電流に応じて電池の起電力が減少しているように見える,というわけです。
もちろんこれだけではなく,電池の素材由来の内部抵抗もあると考えられます。
例題
例題
例題を通じて,電池の内部抵抗の問題について学んでおきましょう。
内部抵抗 を持つ起電力 の乾電池を用いて,以下のような回路を構成した。以下の問いに答えよ。
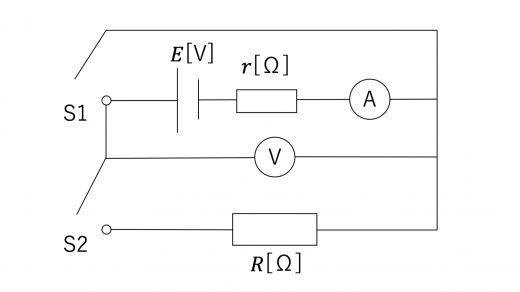
まず,スイッチS1を接続し,スイッチS2は切っておくことを考える。
(1)電流計の数値が ,電流計の数値が を示しているとき, と との間の関係を求めよ。また,この関係を横軸 ,縦軸 としてグラフに書け。
次に,S1を切り,S2を接続する。
(2)電圧計が を示しているとき,電流計が示す数値 を求めよ。
次に,スイッチのオンオフはそのままに,抵抗を可変抵抗に置き換える。
(3)可変抵抗の抵抗値が のとき,この抵抗で消費される電力 を求めよ。
(4) が最大となるような可変抵抗の抵抗値 と,そのときの消費電力の値 を求めよ。
電圧計は非常に抵抗が大きく,電圧計には電流が流れないとしてよい。また,電流計は非常に抵抗が小さく,電流計での電圧降下はないとしてよい。(詳しくは別記事にて解説予定です)
(1)考えるべき回路は以下のようになる。
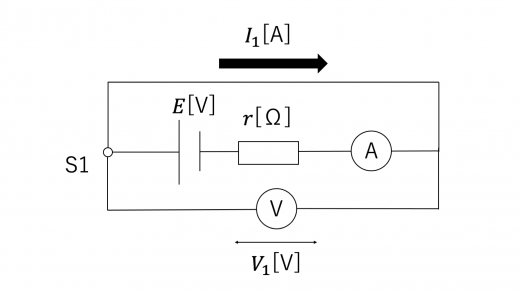
電池の内部抵抗の公式(あるいはキルヒホッフの第2法則)より
これをグラフとして書くと下図のようになる。
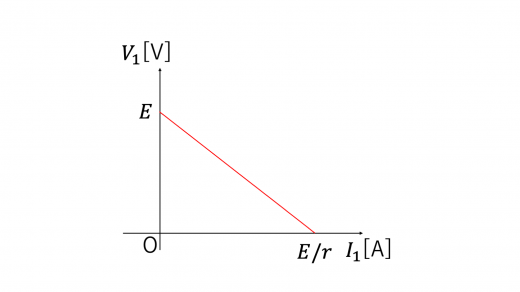
(2)考えるべき回路は以下のようになる。
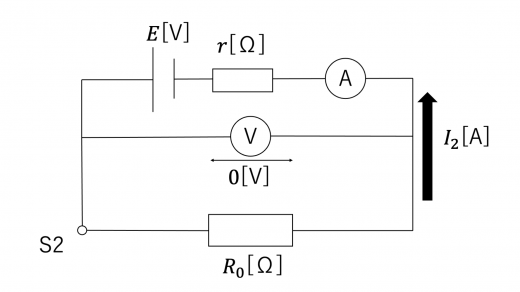
電池の内部抵抗の公式(あるいはキルヒホッフの第2法則)より
(3)回路図は下図のようになる。
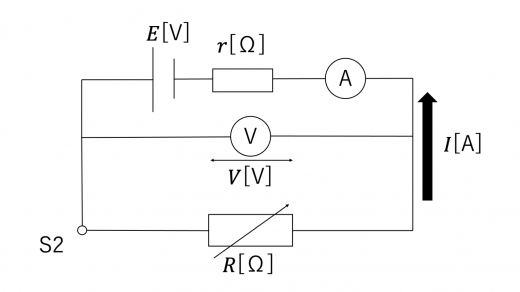
このとき,電池の内部抵抗の公式(あるいはキルヒホッフの第2法則)より,可変抵抗を流れる電流 について,
したがって,可変抵抗で消費される消費電力 は
(4) に注意して
と計算できる。これより, では , では , では が成り立つことがわかる。したがって, は で最大値をとる。
このときの可変抵抗での消費電力は
と求められる。
電池の内部抵抗が絡む問題は,1. 電圧計・電流計が登場することが多い,2. 物理量が文字でおかれることが多いという特徴があります。例題を通して慣れておきましょう。











