円錐振り子とは｜解説と代表例題

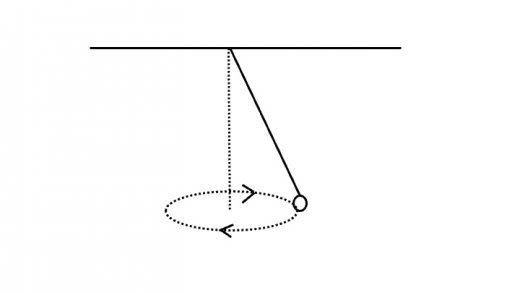
円錐振り子とは一般的には上のような系になります。すなわち，天井に一端を固定されたひもに質点を結び，適当な初速度を与えて点線のように円運動させたものです。ここで，ひもは伸び縮みしない，質点は同一平面上を運動する，という束縛条件があります。

円錐振り子の系では，円運動を考察することが必須になります。円運動については以下の記事を参照してください。
円運動とは｜円運動における加速度・向心力・遠心力

円錐振り子の運動を考察するには，当然まず運動方程式を正しく書くところから始めなければなりません。質点にはたらく力は上図のようになります。

糸の張力と重力がはたらいていますが，まず考えるべきはどの方向の運動方程式を立てるかということです。ここで質点は同一平面内を円運動するのが円錐振り子であるという条件を使います。このことから，鉛直方向の力がつりあっていることがわかります。また，鉛直方向と直交する円運動の向心方向を考えれば，円運動の運動方程式が立てやすいこともわかります。以上より，運動方程式を立てるべきは，鉛直方向と向心方向であることがわかりました。よって張力をこれらの方向に分解するのが定石になります。

よく張力と平行な方向の力がつりあっている，と考えてしまう人がいますが，これは誤りです。円運動を考えてみると向心方向(=張力と平行な方向の成分を持つ方向)に加速度があるので，その方向には力がつりあっていないことがわかります。

以上のことを踏まえて，以下では例題を通して円錐振り子の系を理解していきましょう。

この問題が最も基本的な円錐振り子の例題です。前節の考察を踏まえて，鉛直方向と向心方向の運動方程式を立ててみます。張力を $S$ とおくと，

鉛直方向：　$0=S\cos\theta-mg\qquad (i)$
向心方向： $ml\sin\theta\omega^2=S\sin\theta\qquad (ii)$

ここで円運動の半径は $l\sin\theta$ であることに注意してください。
(i)より $S=\dfrac{mg}{\cos\theta}$ がわかります。これを(ii)に代入すると， $\omega=\sqrt{\dfrac{g}{l\cos\theta}}$ を得ます。

よって求める周期 $T$ と速さ $v$ は $$T=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{l\cos\theta}{g}}\\ v=l\sin\theta\omega=\sqrt{lg\sin\theta\tan\theta}$$ がわかります。

一見円錐振り子に見えない系ですが，これも円錐振り子の亜種とみることができます。なぜなら，半球面から質点が受ける垂直抗力が，一般的な円錐振り子における張力の代わりをしているからです。考えてみると，この問題で質点が受ける力は，円運動の中心軸上のある点に向かう垂直抗力と、重力のみであることがわかり，張力が垂直抗力であること以外は，円錐振り子と全く同じになります。

よって前問と全く同じ考え方が使えます。まず運動方程式を立てると，

鉛直方向：　$0=N\cos\theta-mg\qquad (i)$
向心方向： $mr\omega^2=N\sin\theta\qquad (ii)$

となります。(i)より $N=\dfrac{mg}{\cos\theta}$，これを(ii)に代入して，$\omega=\sqrt{\dfrac{g}{r}\tan\theta}$ がわかります。得られた $\omega$ から $T(\theta)$ を求めると， $$T(\theta)=2\pi\sqrt{\dfrac{r}{g\tan\theta}}$$ となります。$r=l\sin\theta$ とおきなおすと，前問の結果と一致することがわかります。

また求めた結果で単純に $\theta=\dfrac{\pi}{2}$ とおいてはいけません。なぜなら，$r$ も $\theta$ に依存するからです。
正しくは，前問の結果を用いて $$\lim_{\theta\to\frac{\pi}{2}}T(\theta)=\lim_{\theta\to\frac{\pi}{2}}2\pi\sqrt{\dfrac{l\cos\theta}{g}}=0$$ とするのが適切です。$\theta=\dfrac{\pi}{2}$ の時は垂直抗力が鉛直方向成分を持たないため，重力とつりあう力が存在せず，このような結果になると考えられます。