ジュール熱の原理と使い方

ジュール熱とは，「抵抗に電流が流れている際に，その抵抗で消費される熱エネルギー」のことを表しています。

下図のようなモデルを考えることで，ジュール熱が発生する理由を考えてみましょう。

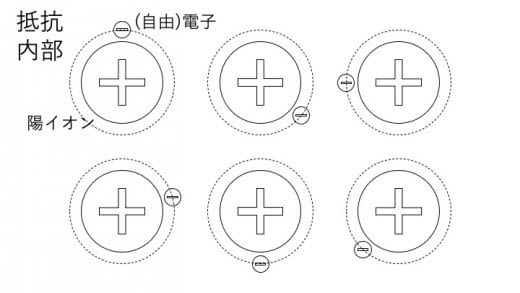
抵抗に電流が流れているとき，その抵抗内には電場が発生していることになり，抵抗内の自由電子は電場により移動することになります。その際，電子は移動する過程で抵抗内の陽イオンに衝突するため，抵抗内の陽イオンは振動することになります。この振動により熱が発生するというわけです。

単位時間に消費されるジュール熱の公式

単位時間に消費されるジュール熱の公式は以下のように表されます。単位は[W]:ワットです。

以下のような簡単な回路を考えてみることで，この公式が成り立っていることを確かめてみましょう。

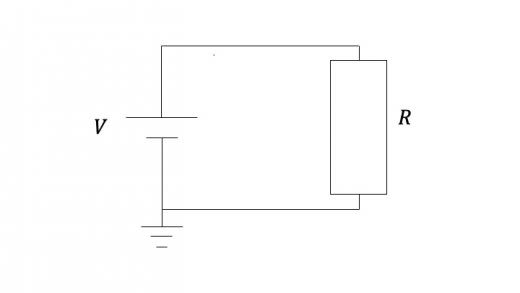
この回路が定常状態になったとき，回路には電流 $I$ が流れているとします。このとき，抵抗に加わっている電圧は $V$ であるから，オームの法則 (詳しくはオームの法則と抵抗の性質) より

$$V = RI \tag{1}$$

が成り立っていることに注意します。

まず，導線と抵抗を系とみなすことで，熱力学第一法則 (詳しくは熱力学第一法則｜仕事と内部エネルギーの関係) より，電池が単位時間に系にもたらす仕事 $W$ と抵抗で消費されるジュール熱 $P$ には

$$W = P \tag{2}$$

という関係が成り立ちます。

ここで，電池が単位時間で押し上げる電荷は $I$ C (クーロン)であるから，電池が単位時間に系にもたらす仕事 $W$ は

$$W = VI \tag{3}$$

(2)式より

$$P = VI$$

(1)式と合わせて

$$P = RI^2 = \dfrac{V^2}{R} =VI$$

を得ることができます。

ジュールの法則

ジュール熱の公式を[J]:ジュールの単位で用いようとする法則の一つがジュールの法則です。以下のような表式で表されます。

これは，ジュール熱が「単位時間に消費されるエネルギー」であることから簡単に導かれます。また，定常電流となっている点に注意してください。このように述べる理由は次の項で説明します。

高校物理の電磁気分野において，ジュール熱は主に，回路とエネルギーの問題において用いられます。

とは言え，抵抗で消費される熱エネルギーが問題で出題される場合，それは問題で考察される時間における熱の総量を問うている場合が多いです。このとき，以下のような場合分けが考えられます。

各時間に抵抗に流れる電流を定式化することが可能な場合

各時間に抵抗に流れる電流が定式化できたり，あるいはグラフが与えられたりしているような場合には，上で示した公式を用いて求めることができます。

定常電流が流れる場合

ジュールの法則を用いて求めることができます。

電流が時々刻々と変化する場合

この場合にはジュールの法則を用いることができませんので，ジュール熱の公式を積分することで求めることになります。

例えば，抵抗 $R$ に流れる電流を $I(t)$ と表されたとします。時刻 $t_0$ から $t_1$ までに抵抗で消費される熱の総量 $Q$ は

$$Q = \int^{t_1}_{t_0} RI^2 dt$$

のように求めることになります。

各時間に抵抗に流れる電流を定式化することが困難な場合

この場合は，ジュール熱の公式，あるいはジュールの法則を用いて求めることができません。 このような時は静電エネルギーの定義・公式｜コンデンサー・球・球殻でも説明したように，熱力学第一法則など，エネルギー保存則を用いて求めることになります。